浙教版八年级下册5.3.2正方形的性质(共17张PPT)
文档属性
| 名称 | 浙教版八年级下册5.3.2正方形的性质(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 176.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-10 09:06:52 | ||
图片预览






文档简介
(共17张PPT)
第五章 特殊平行四边形
5.3.2 正方形的性质
情境导入
在我们的生活中除了平行四边形,矩形,菱形外,还有什么特殊的平行四边形呢?
这些是什么图形?观察它们有什么共同特征?
获取新知
正方形的定义:有一组邻边相等并且有一个角是直角的平行四边形叫做正方形.
正方形既是特殊的矩形,又是特殊的菱形,所以正方形同时具有矩形和菱形的所有性质,于是就有以下定理:
正方形
正方形是特殊的菱形
正方形是特殊的矩形
四条边相等
四个角是直角
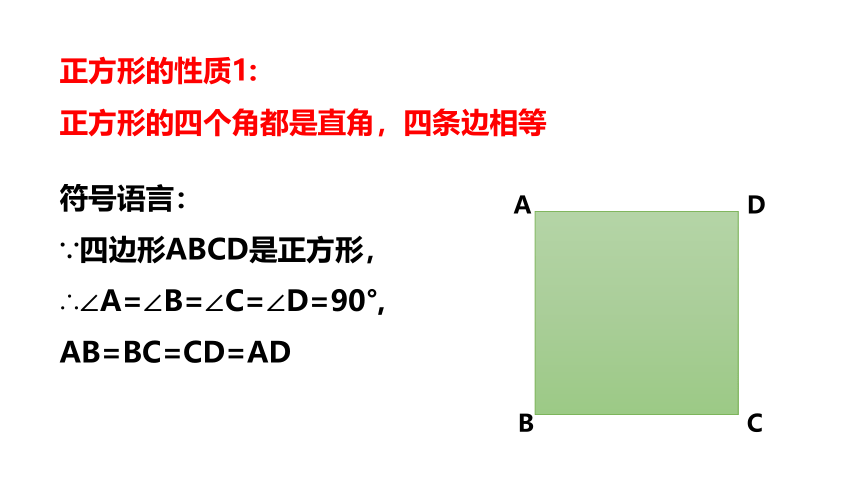
正方形的性质1:正方形的四个角都是直角,四条边相等
正方形的性质1:
正方形的四个角都是直角,四条边相等
A
B
C
D
符号语言:
∵四边形ABCD是正方形,
∴∠A=∠B=∠C=∠D=90°,
AB=BC=CD=AD
拿一张正方形纸片,将它的对角线折叠,你能发现什么?
正方形的两条对角线相等并且互相垂直平分,每一条对角线平分一组对角.
正方形的性质2:
正方形的两条对角线相等并且互相垂直平分,每一条对角线平分一组对角.
A
B
C
D
O
符号语言:
∵四边形ABCD是正方形
∴AC⊥BD,AC=BD,
OA=OB=OC=OD
平行四边形
矩形
菱形
正
方
形
例2 已知:如图,在正方形ABCD中,G是对角线BD上的一点,GE⊥CD,GF⊥BC,E,F分别为垂足,连结AG,EF.
求证:AG=EF.
A
B
C
D
E
G
F
分析 由已知可得,BD平分∠ADC,AD=CD.如果连结CG,那么很容易发现△AGD≌△CGD,得AG=CG.由此我们只需证明四边形FCEG是矩形,就能完成证明.
证明 如图,连结CG.
在△AGD和△CGD中,
∠ADG=∠CDG
(正方形的对角线平分一组对角),
DG=DG,AD=CD
(正方形的四条边相等),
∴△AGD≌△CGD,
∴AG=CG.
A
B
C
D
E
G
F
∵GE⊥CD,GF⊥BC,
∴∠GFC=∠GEC=Rt∠.
又∵∠BCD=Rt∠(正方形的四个角都是直角),
∴四边形FCEG是矩形(有三个角是直角的四边形是矩形),
∴EF=CG(矩形的两条对角线相等),∴AG=EF.
正方形既是轴对称图形,又是中心对称图形,它有四条对称轴且对称轴的交点就是对称中心(即对角线的交点).
直角
正方形
定义
性质
具有一般平行四边形的性质
正方形的特殊性质
(1)正方形的四个角都是________,四条边________.
(2)正方形的对角线____________
______________,每条对角线______________________
相等
相等,并且
互相垂直平分
平分一组对角
随堂演练
1.如图5-3-10,已知正方形ABCD的两条对角线相交于点O,那么此图中等腰直角三角形有 ( )
C
A.4个 B.6个 C.8个 D.10个
2.如图,正方形ABCD的边长为4 cm,则图中阴影部分的面积为
_________cm2.
8
3.如图5-3-14,在正方形ABCD中,E为BC边上一点,F为BA延长线上一点,且CE=AF,连结DE,DF.求证:DE=DF.
证明:在正方形ABCD中,AD=CD,∠DAB=∠C=90°,
∴∠DAF=90°=∠C.
在△DCE和△DAF中,
∴△DCE≌△DAF,∴DE=DF.
第五章 特殊平行四边形
5.3.2 正方形的性质
情境导入
在我们的生活中除了平行四边形,矩形,菱形外,还有什么特殊的平行四边形呢?
这些是什么图形?观察它们有什么共同特征?
获取新知
正方形的定义:有一组邻边相等并且有一个角是直角的平行四边形叫做正方形.
正方形既是特殊的矩形,又是特殊的菱形,所以正方形同时具有矩形和菱形的所有性质,于是就有以下定理:
正方形
正方形是特殊的菱形
正方形是特殊的矩形
四条边相等
四个角是直角
正方形的性质1:正方形的四个角都是直角,四条边相等
正方形的性质1:
正方形的四个角都是直角,四条边相等
A
B
C
D
符号语言:
∵四边形ABCD是正方形,
∴∠A=∠B=∠C=∠D=90°,
AB=BC=CD=AD
拿一张正方形纸片,将它的对角线折叠,你能发现什么?
正方形的两条对角线相等并且互相垂直平分,每一条对角线平分一组对角.
正方形的性质2:
正方形的两条对角线相等并且互相垂直平分,每一条对角线平分一组对角.
A
B
C
D
O
符号语言:
∵四边形ABCD是正方形
∴AC⊥BD,AC=BD,
OA=OB=OC=OD
平行四边形
矩形
菱形
正
方
形
例2 已知:如图,在正方形ABCD中,G是对角线BD上的一点,GE⊥CD,GF⊥BC,E,F分别为垂足,连结AG,EF.
求证:AG=EF.
A
B
C
D
E
G
F
分析 由已知可得,BD平分∠ADC,AD=CD.如果连结CG,那么很容易发现△AGD≌△CGD,得AG=CG.由此我们只需证明四边形FCEG是矩形,就能完成证明.
证明 如图,连结CG.
在△AGD和△CGD中,
∠ADG=∠CDG
(正方形的对角线平分一组对角),
DG=DG,AD=CD
(正方形的四条边相等),
∴△AGD≌△CGD,
∴AG=CG.
A
B
C
D
E
G
F
∵GE⊥CD,GF⊥BC,
∴∠GFC=∠GEC=Rt∠.
又∵∠BCD=Rt∠(正方形的四个角都是直角),
∴四边形FCEG是矩形(有三个角是直角的四边形是矩形),
∴EF=CG(矩形的两条对角线相等),∴AG=EF.
正方形既是轴对称图形,又是中心对称图形,它有四条对称轴且对称轴的交点就是对称中心(即对角线的交点).
直角
正方形
定义
性质
具有一般平行四边形的性质
正方形的特殊性质
(1)正方形的四个角都是________,四条边________.
(2)正方形的对角线____________
______________,每条对角线______________________
相等
相等,并且
互相垂直平分
平分一组对角
随堂演练
1.如图5-3-10,已知正方形ABCD的两条对角线相交于点O,那么此图中等腰直角三角形有 ( )
C
A.4个 B.6个 C.8个 D.10个
2.如图,正方形ABCD的边长为4 cm,则图中阴影部分的面积为
_________cm2.
8
3.如图5-3-14,在正方形ABCD中,E为BC边上一点,F为BA延长线上一点,且CE=AF,连结DE,DF.求证:DE=DF.
证明:在正方形ABCD中,AD=CD,∠DAB=∠C=90°,
∴∠DAF=90°=∠C.
在△DCE和△DAF中,
∴△DCE≌△DAF,∴DE=DF.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
