浙教版数学八年级下册1.2 第2课时 积与商的算术平方根的性质 同步课件(共17张PPT)
文档属性
| 名称 | 浙教版数学八年级下册1.2 第2课时 积与商的算术平方根的性质 同步课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 327.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-10 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
第一章 二次根式
1.2 第2课时 积与商的算术平方根的性质
1.从运算顺序来看
先开方,后平方
先平方,后开方
2.从取值范围来看
a≥0
a取任何实数
=a
3.从运算结果来看
a (a≥ 0)
-a (a<0)
=
=∣a∣
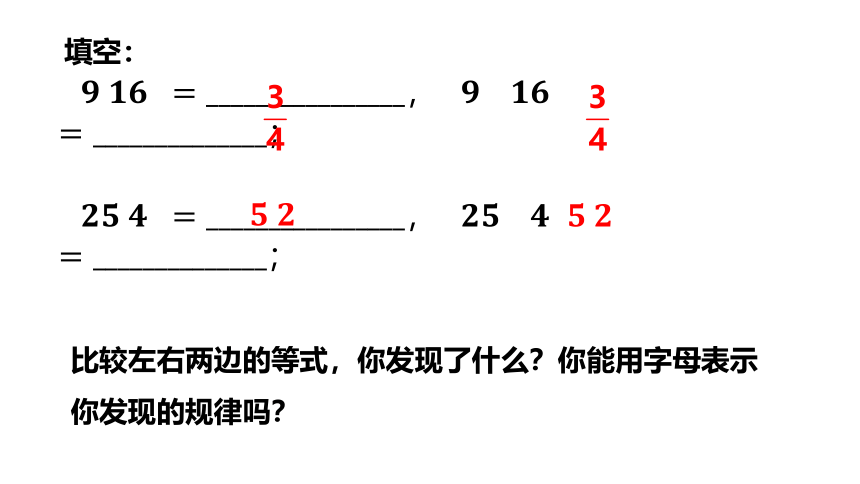
填空:
6
6
比较左右两边的等式,你发现了什么?你能用字母表示你发现的规律吗?
20
20
积的算术平方根的性质:
积的算术平方根,等于积中各因式的算术平方根的积(各因式必须是非负数)
填空:
比较左右两边的等式,你发现了什么?你能用字母表示你发现的规律吗?
商的算术平方根的性质:
商的算术平方根等于被除式的算术平方根除以除式的
算术平方根(被除式必须是非负数,除式必须是正数)。
即
1. 化简 使被开方数不含完全平方的因数.
解:
利用 (a≥0),将这个因数“开方”出来.
我们知道 = ,能否将结果的分母中不含二次根式?
解:
1.被开方数指数小于根指数2;
2.被开方数分解因数(或式)不再含平方数(或平方式).
观察 ,你能发现什么?
像 这样,在根号内不含分母,不含开得尽方的因数或因式,这样的二次根式我们就说它是最简二次根式.
二次根式化简的结果应为最简二次根式.
例1 化简:
解:
化简二次根式的一般步骤
(1)若被开方数是带分数,应先化为假分数;若被开方数是开不尽方的小数,应先化为分数.
(2)化去根号内的分母.
(3)将根号内开得尽方的因数或因式移到根号外.
(4)最后结果是最简二次根式或整式.
例2 化简
B
C
3
B
二次根式的性质
积的算术平方根的性质: =
________(a______0,b______0)
商的算术平方根的性质: =
________(a______0,b______0)
≥
>
≥
≥
第一章 二次根式
1.2 第2课时 积与商的算术平方根的性质
1.从运算顺序来看
先开方,后平方
先平方,后开方
2.从取值范围来看
a≥0
a取任何实数
=a
3.从运算结果来看
a (a≥ 0)
-a (a<0)
=
=∣a∣
填空:
6
6
比较左右两边的等式,你发现了什么?你能用字母表示你发现的规律吗?
20
20
积的算术平方根的性质:
积的算术平方根,等于积中各因式的算术平方根的积(各因式必须是非负数)
填空:
比较左右两边的等式,你发现了什么?你能用字母表示你发现的规律吗?
商的算术平方根的性质:
商的算术平方根等于被除式的算术平方根除以除式的
算术平方根(被除式必须是非负数,除式必须是正数)。
即
1. 化简 使被开方数不含完全平方的因数.
解:
利用 (a≥0),将这个因数“开方”出来.
我们知道 = ,能否将结果的分母中不含二次根式?
解:
1.被开方数指数小于根指数2;
2.被开方数分解因数(或式)不再含平方数(或平方式).
观察 ,你能发现什么?
像 这样,在根号内不含分母,不含开得尽方的因数或因式,这样的二次根式我们就说它是最简二次根式.
二次根式化简的结果应为最简二次根式.
例1 化简:
解:
化简二次根式的一般步骤
(1)若被开方数是带分数,应先化为假分数;若被开方数是开不尽方的小数,应先化为分数.
(2)化去根号内的分母.
(3)将根号内开得尽方的因数或因式移到根号外.
(4)最后结果是最简二次根式或整式.
例2 化简
B
C
3
B
二次根式的性质
积的算术平方根的性质: =
________(a______0,b______0)
商的算术平方根的性质: =
________(a______0,b______0)
≥
>
≥
≥
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
