浙教版数学九年级上册同步课件:4.6 相似多边形(共20张PPT)
文档属性
| 名称 | 浙教版数学九年级上册同步课件:4.6 相似多边形(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1006.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-10 19:23:24 | ||
图片预览








文档简介
(共20张PPT)
第4章 相似三角形
4.6 相似多边形
图形的相似性给人类的创造发明带来灵感.19世纪来法国机械师克莱兰·阿代尔设计的第三架飞行器的形状就是模仿蝙蝠.
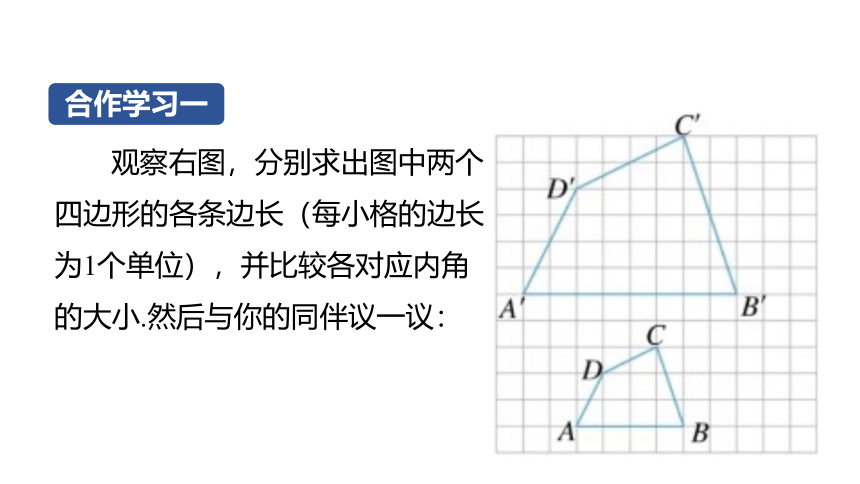
观察右图,分别求出图中两个四边形的各条边长(每小格的边长为1个单位),并比较各对应内角的大小.然后与你的同伴议一议:
合作学习一
(1)这两个四边形的角之间有什么关系
(2)这两个四边形的边之间有什么关系
(3)这两个四边形的形状之间有什么关系
一般地,对应角相等,对应边成比例的两个多边形叫做相似多边形(similar polygon).相似多边形对应边的比也叫做相似比.
获取新知
1.相似多边形的概念
利用相似多边形的定义,我们可以证明两个多边形相似.
例1 矩形纸张的长与宽之比为 ,沿长边对折,所得的矩形纸张是否和原来的矩形纸张相似 请说明理由.
例题讲解
分析:两个矩形,已经有隐含条件四个角相等,只需
证明对边应成比例,要证明两个矩形相似,只需说明
对折所得的矩形邻边之比与原矩形的邻边之比相等.
解 沿长边对折后所得的矩形纸张和原来的矩形纸张相似.理由如下:
如图,原来的纸张为矩形ABCD, = .
在矩形ABFE中,
= = = ,
∴ = ,
连接BC与AD的中点F,E则EF就把矩形ABCD分为全等的两个矩形.
即矩形ABFE与矩形BCDA的对应边成比例.
而两个矩形的对应角相等,
所以矩形ABFE与矩形BCDA相似.
总结:两个矩形相似,只需说明它们的邻边成比例.
议一议
正方形
10
10
菱形
12
12
它们相似吗?
正方形
10
10
矩形
12
8
它们呢?
总结:要证明两个多边形是相似多边形,就要证明它们的对应角相等,对应边成比例.
合作学习二
1、如图:四边形A1B1 C1D1与四边形ABCD相似,相似比是k,求这两个四边形的周长比.
2、(1)连结第一题图两个相似四边形的对角线BD,B1D1,所得的△CBD和△C1B1D1相似么?另外的一对三角形是否也相似呢?相似比是多少?
(2)这两个四边形
的面积之比与相似比有什么关系?
与相似三角形类似,相似多边形有以下的性质:
相似多边形的周长之比等于相似比;相似多边形的面积之比等于相似比的平方.
2.相似多边形的性质
1、两个相似多边形的一组对应边分别为4cm和6cm,则他们的周长之比为 ,面积之比为 .
2、若两菱形相似,相似比为2:3,周长之差为13cm,则两个菱形的边长分别为 .
做一做
2:3
4:9
解析:∵两个相似菱形的相似比为2:3,
∴周长之比为2:3,
26cm和39cm
设一个菱形的周长为2x,则另一个菱形的周长为3x,
由题意得,3x-2x=13,
解得,x=13,
2x=26,3x=39,
则这两个菱形的周长分别为26cm和39cm,
故答案为:26cm和39cm.
例2 如图,已知矩形ABCD与矩形DEFC相似,且AB=2 cm,BC=5 cm,求AE的长.
总结:利用相似多边形的性质进行计算的关键点首先弄清楚哪些边是对应边,哪些角是对应角,然后根据相似多边形的性质列式求解.
如图,从四边形ABCD到四边形A'B'C'D'的改变过程中,图形的形状没有改变.一般地,由一个图形改变为另一个图形,在改变的过程中保持形状不变(大小可以改变),这样的图形改变叫做图形的相似.
3.图形的相似的概念
对应顶点的字母写在对应的位置上
图形的相似在人们的生活中有着广泛的应用.例如地图的绘制,照片的放大与缩小(如图)等都是图形的相似的应用.
相似比的平方
相似比
第4章 相似三角形
4.6 相似多边形
图形的相似性给人类的创造发明带来灵感.19世纪来法国机械师克莱兰·阿代尔设计的第三架飞行器的形状就是模仿蝙蝠.
观察右图,分别求出图中两个四边形的各条边长(每小格的边长为1个单位),并比较各对应内角的大小.然后与你的同伴议一议:
合作学习一
(1)这两个四边形的角之间有什么关系
(2)这两个四边形的边之间有什么关系
(3)这两个四边形的形状之间有什么关系
一般地,对应角相等,对应边成比例的两个多边形叫做相似多边形(similar polygon).相似多边形对应边的比也叫做相似比.
获取新知
1.相似多边形的概念
利用相似多边形的定义,我们可以证明两个多边形相似.
例1 矩形纸张的长与宽之比为 ,沿长边对折,所得的矩形纸张是否和原来的矩形纸张相似 请说明理由.
例题讲解
分析:两个矩形,已经有隐含条件四个角相等,只需
证明对边应成比例,要证明两个矩形相似,只需说明
对折所得的矩形邻边之比与原矩形的邻边之比相等.
解 沿长边对折后所得的矩形纸张和原来的矩形纸张相似.理由如下:
如图,原来的纸张为矩形ABCD, = .
在矩形ABFE中,
= = = ,
∴ = ,
连接BC与AD的中点F,E则EF就把矩形ABCD分为全等的两个矩形.
即矩形ABFE与矩形BCDA的对应边成比例.
而两个矩形的对应角相等,
所以矩形ABFE与矩形BCDA相似.
总结:两个矩形相似,只需说明它们的邻边成比例.
议一议
正方形
10
10
菱形
12
12
它们相似吗?
正方形
10
10
矩形
12
8
它们呢?
总结:要证明两个多边形是相似多边形,就要证明它们的对应角相等,对应边成比例.
合作学习二
1、如图:四边形A1B1 C1D1与四边形ABCD相似,相似比是k,求这两个四边形的周长比.
2、(1)连结第一题图两个相似四边形的对角线BD,B1D1,所得的△CBD和△C1B1D1相似么?另外的一对三角形是否也相似呢?相似比是多少?
(2)这两个四边形
的面积之比与相似比有什么关系?
与相似三角形类似,相似多边形有以下的性质:
相似多边形的周长之比等于相似比;相似多边形的面积之比等于相似比的平方.
2.相似多边形的性质
1、两个相似多边形的一组对应边分别为4cm和6cm,则他们的周长之比为 ,面积之比为 .
2、若两菱形相似,相似比为2:3,周长之差为13cm,则两个菱形的边长分别为 .
做一做
2:3
4:9
解析:∵两个相似菱形的相似比为2:3,
∴周长之比为2:3,
26cm和39cm
设一个菱形的周长为2x,则另一个菱形的周长为3x,
由题意得,3x-2x=13,
解得,x=13,
2x=26,3x=39,
则这两个菱形的周长分别为26cm和39cm,
故答案为:26cm和39cm.
例2 如图,已知矩形ABCD与矩形DEFC相似,且AB=2 cm,BC=5 cm,求AE的长.
总结:利用相似多边形的性质进行计算的关键点首先弄清楚哪些边是对应边,哪些角是对应角,然后根据相似多边形的性质列式求解.
如图,从四边形ABCD到四边形A'B'C'D'的改变过程中,图形的形状没有改变.一般地,由一个图形改变为另一个图形,在改变的过程中保持形状不变(大小可以改变),这样的图形改变叫做图形的相似.
3.图形的相似的概念
对应顶点的字母写在对应的位置上
图形的相似在人们的生活中有着广泛的应用.例如地图的绘制,照片的放大与缩小(如图)等都是图形的相似的应用.
相似比的平方
相似比
同课章节目录
