浙教版九年级上册1.2二次函数y=ax2+bx+c的图象( 第3课时)课件((共14张PPT))
文档属性
| 名称 | 浙教版九年级上册1.2二次函数y=ax2+bx+c的图象( 第3课时)课件((共14张PPT)) |

|
|
| 格式 | pptx | ||
| 文件大小 | 277.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-11 00:00:00 | ||
图片预览






文档简介
(共14张PPT)
1.2 第3课时 二次函数y=ax +bx+c的图象
第1章 二次函数
y=ax2
y=a(x-h)2 +k
上正下负
左加右减
一般地,二次函数y=a(x-h)2 +k与y=ax2的________相同,_______不同.
形状
位置
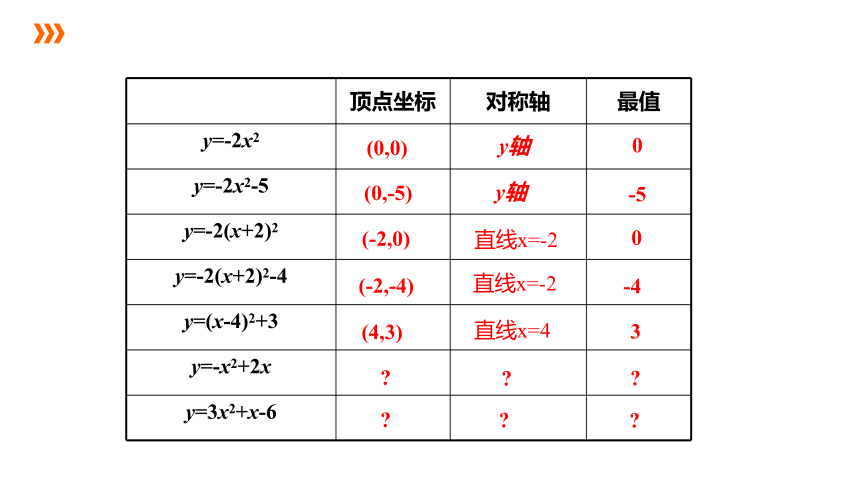
顶点坐标 对称轴 最值
y=-2x2
y=-2x2-5
y=-2(x+2)2
y=-2(x+2)2-4
y=(x-4)2+3
y=-x2+2x
y=3x2+x-6
(0,0)
y轴
0
(0,-5)
y轴
-5
(-2,0)
直线x=-2
0
(-2,-4)
直线x=-2
-4
(4,3)
直线x=4
3
获取新知
如何用配方法将一般式 y=ax2+bx+c(a≠0)化成顶点式 y=a(x-h)2+k?
配方:
提取二次项系数
配方:加上再减去一次项系数绝对值一半的平方
整理:前三项化为和的平方形式,后两项合并同类项
化简:去掉中括号
例题讲解
解:
例1 求抛物线 的对称轴和顶点坐标.
因此,抛物线的对称轴是直线x=3,顶点坐标是(3,2).
例2 已知函数y=- x2+4x-3 ,回答下列问题:
(1)函数y=- x2+4x-3的图象能否由函数y=- x2的图象通过平移得到 若能,请说出平移的过程,并画出示意图.
(2)说出函数图象的开口方向、对称轴和顶点坐标.
解: (1) 原函数可以化为y=- (x-4)2+5.
函数y=- x2+4x-3的图象可由函数y=- x2的图象先向右平移4个单位,再向上平移5个单位得到.示意图如图.
(2)原函数可以化为y=- (x-4)2+5.
函数图象的开口方向向下,对称轴是直线x=4,
顶点坐标是(4,5).
随堂演练
1.抛物线y=x2+2x+3的对称轴是( )
A.直线x=1 B.直线x=-1
C.直线x=-2 D.直线x=2
2.抛物线y=x2-2x+1的顶点坐标是( )
A.(1,0) B.(-1,0)
C.(-2,1) D.(2,-1)
B
A
3.已知抛物线y=x2+4x+5.
(1)求其顶点坐标及对称轴;
(2)请说明如何平移该抛物线才能得到抛物线y=x2.
解:(1)∵y=x2+4x+5=(x+2)2+1,
∴抛物线y=(x+2)2+1的顶点坐标为(-2,1),对称轴为直线x=-2.
(2)将抛物线y=x2+4x+5向右平移2个单位,再向下平移1个单位可得到抛物线y=x2(答案不唯一).
4.根据已知条件,求下列抛物线的函数表达式:
(1)抛物线的顶点是(3,-1),且过点(2,3);
解:(1)∵抛物线的顶点坐标为(3,-1),
∴设抛物线的函数表达式为y=a(x-3)2-1(a≠0).
把(2,3)代入,得a=4,
∴抛物线的函数表达式为y=4(x-3)2-1=4x2-24x+35.
(2)抛物线过(0,1),(-1,0),(1,0)三点;
解:(2)设抛物线的函数表达式为y=ax2+bx+c(a≠0).
将(0,1),(-1,0),(1,0)代入,得:
∴抛物线的函数表达式为y=-x2+1.
(3)抛物线的对称轴是直线x=2,且过点(1,4)和(5,0).
解:(3)设抛物线的函数表达式为y=ax2+bx+c(a≠0).
∴抛物线的函数表达式为 .
顶点:
对称轴:
y=ax2+bx+c(a ≠0)
(一般式)
公式法
(顶点式)
配方法
1.2 第3课时 二次函数y=ax +bx+c的图象
第1章 二次函数
y=ax2
y=a(x-h)2 +k
上正下负
左加右减
一般地,二次函数y=a(x-h)2 +k与y=ax2的________相同,_______不同.
形状
位置
顶点坐标 对称轴 最值
y=-2x2
y=-2x2-5
y=-2(x+2)2
y=-2(x+2)2-4
y=(x-4)2+3
y=-x2+2x
y=3x2+x-6
(0,0)
y轴
0
(0,-5)
y轴
-5
(-2,0)
直线x=-2
0
(-2,-4)
直线x=-2
-4
(4,3)
直线x=4
3
获取新知
如何用配方法将一般式 y=ax2+bx+c(a≠0)化成顶点式 y=a(x-h)2+k?
配方:
提取二次项系数
配方:加上再减去一次项系数绝对值一半的平方
整理:前三项化为和的平方形式,后两项合并同类项
化简:去掉中括号
例题讲解
解:
例1 求抛物线 的对称轴和顶点坐标.
因此,抛物线的对称轴是直线x=3,顶点坐标是(3,2).
例2 已知函数y=- x2+4x-3 ,回答下列问题:
(1)函数y=- x2+4x-3的图象能否由函数y=- x2的图象通过平移得到 若能,请说出平移的过程,并画出示意图.
(2)说出函数图象的开口方向、对称轴和顶点坐标.
解: (1) 原函数可以化为y=- (x-4)2+5.
函数y=- x2+4x-3的图象可由函数y=- x2的图象先向右平移4个单位,再向上平移5个单位得到.示意图如图.
(2)原函数可以化为y=- (x-4)2+5.
函数图象的开口方向向下,对称轴是直线x=4,
顶点坐标是(4,5).
随堂演练
1.抛物线y=x2+2x+3的对称轴是( )
A.直线x=1 B.直线x=-1
C.直线x=-2 D.直线x=2
2.抛物线y=x2-2x+1的顶点坐标是( )
A.(1,0) B.(-1,0)
C.(-2,1) D.(2,-1)
B
A
3.已知抛物线y=x2+4x+5.
(1)求其顶点坐标及对称轴;
(2)请说明如何平移该抛物线才能得到抛物线y=x2.
解:(1)∵y=x2+4x+5=(x+2)2+1,
∴抛物线y=(x+2)2+1的顶点坐标为(-2,1),对称轴为直线x=-2.
(2)将抛物线y=x2+4x+5向右平移2个单位,再向下平移1个单位可得到抛物线y=x2(答案不唯一).
4.根据已知条件,求下列抛物线的函数表达式:
(1)抛物线的顶点是(3,-1),且过点(2,3);
解:(1)∵抛物线的顶点坐标为(3,-1),
∴设抛物线的函数表达式为y=a(x-3)2-1(a≠0).
把(2,3)代入,得a=4,
∴抛物线的函数表达式为y=4(x-3)2-1=4x2-24x+35.
(2)抛物线过(0,1),(-1,0),(1,0)三点;
解:(2)设抛物线的函数表达式为y=ax2+bx+c(a≠0).
将(0,1),(-1,0),(1,0)代入,得:
∴抛物线的函数表达式为y=-x2+1.
(3)抛物线的对称轴是直线x=2,且过点(1,4)和(5,0).
解:(3)设抛物线的函数表达式为y=ax2+bx+c(a≠0).
∴抛物线的函数表达式为 .
顶点:
对称轴:
y=ax2+bx+c(a ≠0)
(一般式)
公式法
(顶点式)
配方法
同课章节目录
