浙教版数学九年级上册同步课件:2.4 概率的简单应用(共17张PPT)
文档属性
| 名称 | 浙教版数学九年级上册同步课件:2.4 概率的简单应用(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 468.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-10 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
第2章 简单事件的概率
2.4 概率的简单应用
买彩票的人一定希望知道中奖的概率有多大.怎样来估计彩票中奖的概率呢
例1 某商场举办有奖销售活动,每张奖券获奖的可能性相同.以每10000张奖券为一个开奖单位,设特等奖1个,一等奖10个,二等奖100个.问1张奖券中一等奖的概率是多少?中奖的概率是多少?
例题讲解
解 因为10000张奖券中能中一等奖的张数是10张,所以1张奖券中一等奖的概率 .
又因为10000张奖券中能中奖的奖券总数是1+10+100=111(张),所以1张奖券中奖的概率 .
答:1张奖券中一等奖的概率是 ,中奖的概率 .
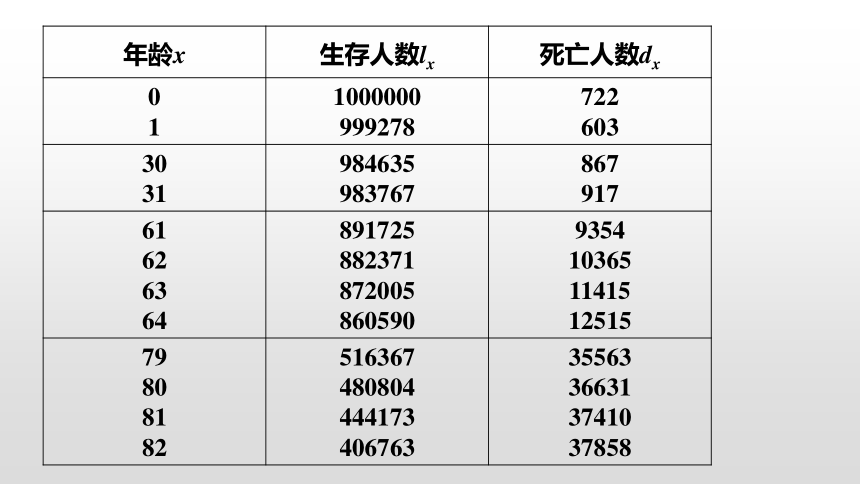
例2 下表是中国人民银行发布的中国人寿保险经验你生命表(2000~2003年)男性表的部分摘录.根据下表估算下列概率(结果精确到0.0001).
(1)某人今年61岁,他当年死亡的概率.
(2)某人今年31岁,他活到62岁的概率.
年龄x 生存人数lx 死亡人数dx
0 1 1000000 999278 722
603
30 31 984635 983767 867
917
61 62 63 64 891725 882371 872005 860590 9354
10365
11415
12515
79 80 81 82 516367 480804 444173 406763 35563
36631
37410
37858
解 (1)根据上表,61岁的生存人数l61=891725,61岁的死亡人数d61=9354,
所以所求概率
答:他当年死亡的概率约为0.0125.
(2)根据生命表,l31=983767,l62=882371,
所以所求概率 .
答:他活到62岁的概率约为0.8969.
例3 小亮和小芳都想参加学校杜团组织的暑假实践活动,但只有一个名额,小亮提议用如下的办法决定谁去参加活动:将一个转盘9等分,分别标上1至9九个号码,随意转动转盘,若转到2的倍数,小亮去参加活动;转到3的倍数,小芳去参加活动;转到其它号码则重新转动转盘.
(1)转盘转到2的倍数的概率是多少?
(2)你认为这个游戏公平吗?请说明理由.
解:(1)∵共有9种等可能的结果,其中2的倍数有4个,
(2)游戏不公平,
∵共有9种等可能的结果,其中3的倍数有3个,
∴游戏不公平
游戏是否的标准:
两者的概率相等,则游戏公平;否则游戏不公平
1.某商场为了吸引顾客,设立了可以自由转动的转盘(如图,转盘被均匀分为20份),并规定:顾客每购买200元的商品,就能获得一次转动转盘的机会,如果转盘停止转动后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得200元、100元、50元的购物券,凭购物券可以在该商场继续购物;如果顾客不愿意转转盘,那么可以直接获得购物券30元.
(1)求转动一次转盘获得购物券的概率;
(2)转转盘和直接获得购物券,你认为选择哪种方式对顾客更合算?
随堂演练
2.如图所示,一个转盘被平均分成六个扇形,并在上面依次写上数字1、2、3、4、5、6;若自由转动转盘,当它停止转动时,求:
(1)指针指向4的概率_____;(直接写出答案)
(2)指针指向数字是奇数的概率____;(直接写出答案)
(3)指针指向数字不小于5的概率_____;(直接写出答案)
(4)现只有一张电影票,小王和小李都想去看,请你利用这个转盘,设计一个公平的游戏规则.
解:(1)∵自由转动转盘,当它停止转动时指针指向的
数字有6种等可能结果,其中指针指向3的只有1种,
∴指针指向4的概率为
(2)∵自由转动转盘,当它停止转动时指针指向的数字有6种等可能结果,其中指针指向数字是偶数的有1、3、5三种结果,
∴指针指向数字是奇数的概率为
(3)∵自由转动转盘,当它停止转动时指针指向的数字有6种等可能结果,其中指针指向数字不小于5的有5、6两种结果,
∴指针指向数字不小于5的概率为
(4)自由转动转盘,当它停止转动时,指针指向数字是偶数时小王胜,否则小李胜.
思维拓展
九(1)班组织班级联谊会,最后进入抽奖环节,每名同学都有一次抽奖机会,抽奖方案如下:将一副扑克牌中数字为“2”“3”“3”“5”“6”的5张牌背面朝上洗匀,先从中抽出1张牌,再从余下的4张牌中抽出1张牌,记录两张牌的数字后放回,完成一次抽奖.记每次抽出2张牌的数字之差为x,按表格要求确定奖项.
奖项 一等奖 二等奖 三等奖
|x| |x|=4 |x|=3 1≤|x|<3
(1)用列表或画树状图的方法求出甲同学抽奖一次获得一等奖的概率;
(2)是否每次抽奖都会获奖,为什么?
解:(1)画树状图如下:
∵共有20种等可能的情况,甲同学抽奖一次获得一等奖的有2种情况,
∴甲同学抽奖一次获得一等奖的概率为 .
(2)不一定.理由:当抽出的两张牌的数字都是3时,|x|=0,不会获奖.
第2章 简单事件的概率
2.4 概率的简单应用
买彩票的人一定希望知道中奖的概率有多大.怎样来估计彩票中奖的概率呢
例1 某商场举办有奖销售活动,每张奖券获奖的可能性相同.以每10000张奖券为一个开奖单位,设特等奖1个,一等奖10个,二等奖100个.问1张奖券中一等奖的概率是多少?中奖的概率是多少?
例题讲解
解 因为10000张奖券中能中一等奖的张数是10张,所以1张奖券中一等奖的概率 .
又因为10000张奖券中能中奖的奖券总数是1+10+100=111(张),所以1张奖券中奖的概率 .
答:1张奖券中一等奖的概率是 ,中奖的概率 .
例2 下表是中国人民银行发布的中国人寿保险经验你生命表(2000~2003年)男性表的部分摘录.根据下表估算下列概率(结果精确到0.0001).
(1)某人今年61岁,他当年死亡的概率.
(2)某人今年31岁,他活到62岁的概率.
年龄x 生存人数lx 死亡人数dx
0 1 1000000 999278 722
603
30 31 984635 983767 867
917
61 62 63 64 891725 882371 872005 860590 9354
10365
11415
12515
79 80 81 82 516367 480804 444173 406763 35563
36631
37410
37858
解 (1)根据上表,61岁的生存人数l61=891725,61岁的死亡人数d61=9354,
所以所求概率
答:他当年死亡的概率约为0.0125.
(2)根据生命表,l31=983767,l62=882371,
所以所求概率 .
答:他活到62岁的概率约为0.8969.
例3 小亮和小芳都想参加学校杜团组织的暑假实践活动,但只有一个名额,小亮提议用如下的办法决定谁去参加活动:将一个转盘9等分,分别标上1至9九个号码,随意转动转盘,若转到2的倍数,小亮去参加活动;转到3的倍数,小芳去参加活动;转到其它号码则重新转动转盘.
(1)转盘转到2的倍数的概率是多少?
(2)你认为这个游戏公平吗?请说明理由.
解:(1)∵共有9种等可能的结果,其中2的倍数有4个,
(2)游戏不公平,
∵共有9种等可能的结果,其中3的倍数有3个,
∴游戏不公平
游戏是否的标准:
两者的概率相等,则游戏公平;否则游戏不公平
1.某商场为了吸引顾客,设立了可以自由转动的转盘(如图,转盘被均匀分为20份),并规定:顾客每购买200元的商品,就能获得一次转动转盘的机会,如果转盘停止转动后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得200元、100元、50元的购物券,凭购物券可以在该商场继续购物;如果顾客不愿意转转盘,那么可以直接获得购物券30元.
(1)求转动一次转盘获得购物券的概率;
(2)转转盘和直接获得购物券,你认为选择哪种方式对顾客更合算?
随堂演练
2.如图所示,一个转盘被平均分成六个扇形,并在上面依次写上数字1、2、3、4、5、6;若自由转动转盘,当它停止转动时,求:
(1)指针指向4的概率_____;(直接写出答案)
(2)指针指向数字是奇数的概率____;(直接写出答案)
(3)指针指向数字不小于5的概率_____;(直接写出答案)
(4)现只有一张电影票,小王和小李都想去看,请你利用这个转盘,设计一个公平的游戏规则.
解:(1)∵自由转动转盘,当它停止转动时指针指向的
数字有6种等可能结果,其中指针指向3的只有1种,
∴指针指向4的概率为
(2)∵自由转动转盘,当它停止转动时指针指向的数字有6种等可能结果,其中指针指向数字是偶数的有1、3、5三种结果,
∴指针指向数字是奇数的概率为
(3)∵自由转动转盘,当它停止转动时指针指向的数字有6种等可能结果,其中指针指向数字不小于5的有5、6两种结果,
∴指针指向数字不小于5的概率为
(4)自由转动转盘,当它停止转动时,指针指向数字是偶数时小王胜,否则小李胜.
思维拓展
九(1)班组织班级联谊会,最后进入抽奖环节,每名同学都有一次抽奖机会,抽奖方案如下:将一副扑克牌中数字为“2”“3”“3”“5”“6”的5张牌背面朝上洗匀,先从中抽出1张牌,再从余下的4张牌中抽出1张牌,记录两张牌的数字后放回,完成一次抽奖.记每次抽出2张牌的数字之差为x,按表格要求确定奖项.
奖项 一等奖 二等奖 三等奖
|x| |x|=4 |x|=3 1≤|x|<3
(1)用列表或画树状图的方法求出甲同学抽奖一次获得一等奖的概率;
(2)是否每次抽奖都会获奖,为什么?
解:(1)画树状图如下:
∵共有20种等可能的情况,甲同学抽奖一次获得一等奖的有2种情况,
∴甲同学抽奖一次获得一等奖的概率为 .
(2)不一定.理由:当抽出的两张牌的数字都是3时,|x|=0,不会获奖.
同课章节目录
