浙教版数学九年级上册同步课件:1.4 第3课时 二次函数与一元二次方程(共10张PPT)
文档属性
| 名称 | 浙教版数学九年级上册同步课件:1.4 第3课时 二次函数与一元二次方程(共10张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 172.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-10 19:48:27 | ||
图片预览


文档简介
(共10张PPT)
第1章 二次函数
1.4二次函数的应用
第3课时 二次函数与一元二次方程
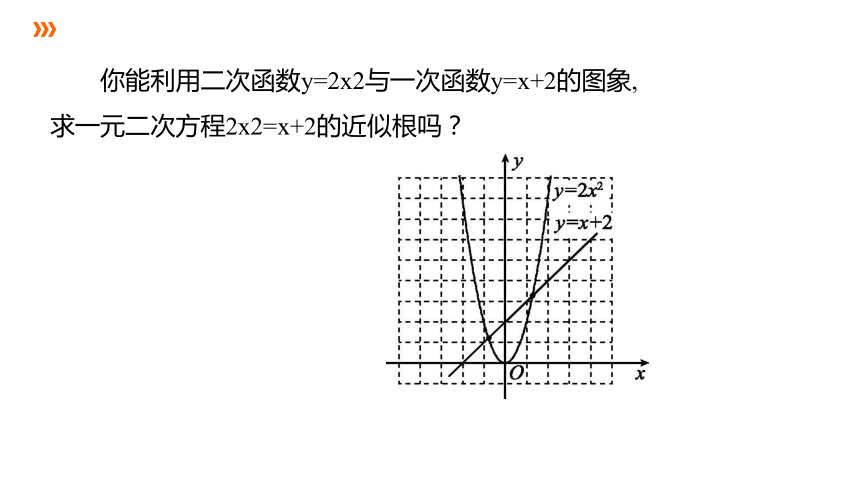
你能利用二次函数y=2x2与一次函数y=x+2的图象,求一元二次方程2x2=x+2的近似根吗?
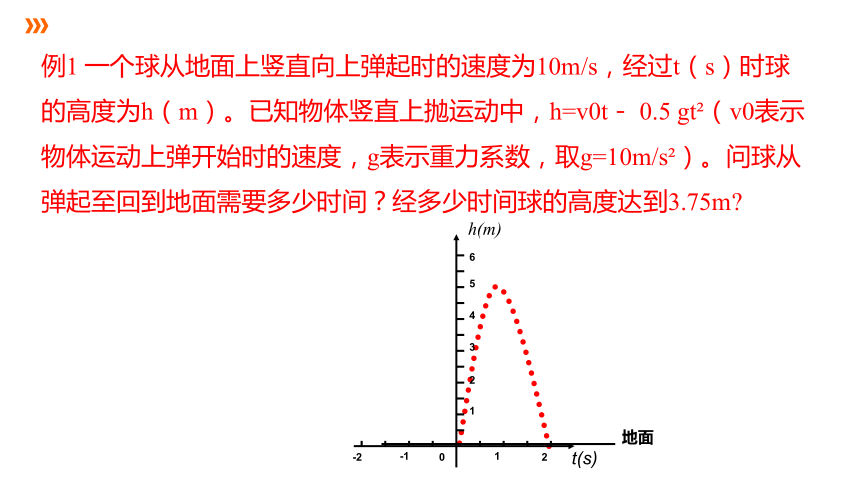
例1 一个球从地面上竖直向上弹起时的速度为10m/s,经过t(s)时球的高度为h(m)。已知物体竖直上抛运动中,h=v0t- 0.5 gt (v0表示物体运动上弹开始时的速度,g表示重力系数,取g=10m/s )。问球从弹起至回到地面需要多少时间?经多少时间球的高度达到3.75m
地面
1
2
0
-1
-2
t(s)
1
2
3
4
5
6
h(m)
地面
1
2
0
-1
-2
t(s)
1
2
3
4
5
6
h(m)
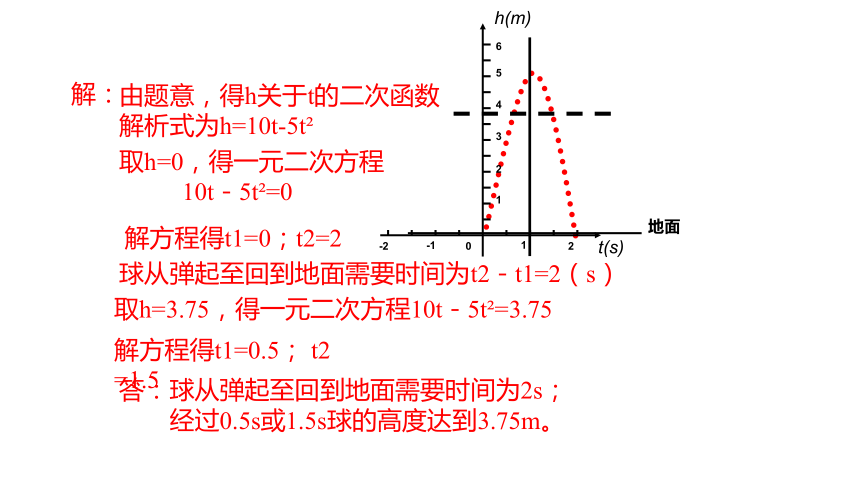
解:
由题意,得h关于t的二次函数
解析式为h=10t-5t
取h=0,得一元二次方程
10t-5t =0
解方程得t1=0;t2=2
球从弹起至回到地面需要时间为t2-t1=2(s)
取h=3.75,得一元二次方程10t-5t =3.75
解方程得t1=0.5; t2 =1.5
答:球从弹起至回到地面需要时间为2s;
经过0.5s或1.5s球的高度达到3.75m。
二次函数的图象与x轴有没有交点,由什么决定
由b -4ac的符号决定
b -4ac >0,有两个交点
b -4ac =0,只有一个交点
b -4ac <0,没有交点
下列函数图象与x轴有没有交点。
①x =2x-1 ②2x -x+1=0 ③2x -4x-1=0
只有一个交点
没有交点
有两个交点
忆一忆
例2 利用二次函数的图象求一元二次方程
x +x-1= 0 的近似解。
1
2
0
-1
-2
x
1
2
3
4
5
6
y
y=x
y=1-x
解:
随堂演练
1. 抛物线y=ax2+bx+c的对称轴是直线x=﹣2.抛物线与x
轴的一个交点在点(﹣4,0)和点(﹣3,0)之间,其
部分图象如图所示,下列结论中正确的个数有( )①4a﹣b=0;②c≤3a;③关于x的方程ax2+bx+c=2有两个不相等实数根;④b2+2b>4ac.
A.1个 B.2个 C.3个 D.4个
C
2. 抛物线y=2x2+2(k﹣1)x﹣k(k为常数)与x轴交点的个数是 .
2
3. 如图,已知y=x2-x-3的图象,请求出方程x2-x-3=0的近似解.
解:观察函数y=x2-x-3图象得图象与x轴的交点分别是
(-1.5,0),(2.5,0),方程x2-x-3=0的近似解是
x1≈-1.5,x2≈2.5.
二次函数
y=ax +bx+c
y=0
一元二次方程ax +bx+c=0
则
函数与x轴交点坐标为:
(m,0);(n,0)
两根为x1=m;x2=n
反过来,也可利用二次函数的图象求一元二次方程的解。
第1章 二次函数
1.4二次函数的应用
第3课时 二次函数与一元二次方程
你能利用二次函数y=2x2与一次函数y=x+2的图象,求一元二次方程2x2=x+2的近似根吗?
例1 一个球从地面上竖直向上弹起时的速度为10m/s,经过t(s)时球的高度为h(m)。已知物体竖直上抛运动中,h=v0t- 0.5 gt (v0表示物体运动上弹开始时的速度,g表示重力系数,取g=10m/s )。问球从弹起至回到地面需要多少时间?经多少时间球的高度达到3.75m
地面
1
2
0
-1
-2
t(s)
1
2
3
4
5
6
h(m)
地面
1
2
0
-1
-2
t(s)
1
2
3
4
5
6
h(m)
解:
由题意,得h关于t的二次函数
解析式为h=10t-5t
取h=0,得一元二次方程
10t-5t =0
解方程得t1=0;t2=2
球从弹起至回到地面需要时间为t2-t1=2(s)
取h=3.75,得一元二次方程10t-5t =3.75
解方程得t1=0.5; t2 =1.5
答:球从弹起至回到地面需要时间为2s;
经过0.5s或1.5s球的高度达到3.75m。
二次函数的图象与x轴有没有交点,由什么决定
由b -4ac的符号决定
b -4ac >0,有两个交点
b -4ac =0,只有一个交点
b -4ac <0,没有交点
下列函数图象与x轴有没有交点。
①x =2x-1 ②2x -x+1=0 ③2x -4x-1=0
只有一个交点
没有交点
有两个交点
忆一忆
例2 利用二次函数的图象求一元二次方程
x +x-1= 0 的近似解。
1
2
0
-1
-2
x
1
2
3
4
5
6
y
y=x
y=1-x
解:
随堂演练
1. 抛物线y=ax2+bx+c的对称轴是直线x=﹣2.抛物线与x
轴的一个交点在点(﹣4,0)和点(﹣3,0)之间,其
部分图象如图所示,下列结论中正确的个数有( )①4a﹣b=0;②c≤3a;③关于x的方程ax2+bx+c=2有两个不相等实数根;④b2+2b>4ac.
A.1个 B.2个 C.3个 D.4个
C
2. 抛物线y=2x2+2(k﹣1)x﹣k(k为常数)与x轴交点的个数是 .
2
3. 如图,已知y=x2-x-3的图象,请求出方程x2-x-3=0的近似解.
解:观察函数y=x2-x-3图象得图象与x轴的交点分别是
(-1.5,0),(2.5,0),方程x2-x-3=0的近似解是
x1≈-1.5,x2≈2.5.
二次函数
y=ax +bx+c
y=0
一元二次方程ax +bx+c=0
则
函数与x轴交点坐标为:
(m,0);(n,0)
两根为x1=m;x2=n
反过来,也可利用二次函数的图象求一元二次方程的解。
同课章节目录
