浙教版数学九年级上册同步课件:2.3 用频率估计概率(共19张PPT)
文档属性
| 名称 | 浙教版数学九年级上册同步课件:2.3 用频率估计概率(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 477.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-10 20:35:40 | ||
图片预览




文档简介
(共19张PPT)
第2章 简单事件的概率
2.3 用频率估计概率
提高运动员的罚球命中率是篮球教练需考虑的问题之一.你认为可以如何估计一位篮球运动员的罚球命中率
问题1 抛掷一枚均匀硬币,硬币落地后,会出现哪些可能的结果呢?
问题2 它们的概率是多少呢?
出现“正面朝上”和“反面朝上”两种情况
都是
问题3 在实际掷硬币时,会出现什么情况呢?
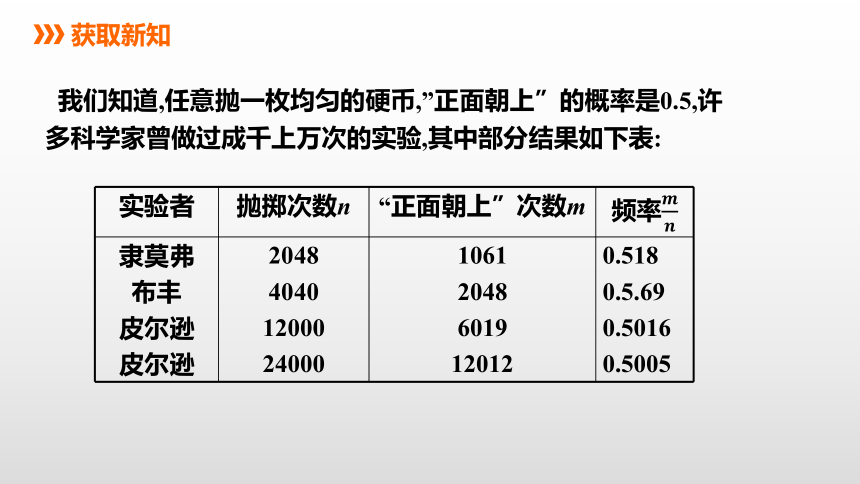
我们知道,任意抛一枚均匀的硬币,”正面朝上”的概率是0.5,许多科学家曾做过成千上万次的实验,其中部分结果如下表:
实验者 抛掷次数n “正面朝上”次数m 频率
隶莫弗 布丰 皮尔逊 皮尔逊 2048 4040 12000 24000 1061 2048 6019 12012 0.518
0.5.69
0.5016
0.5005
获取新知
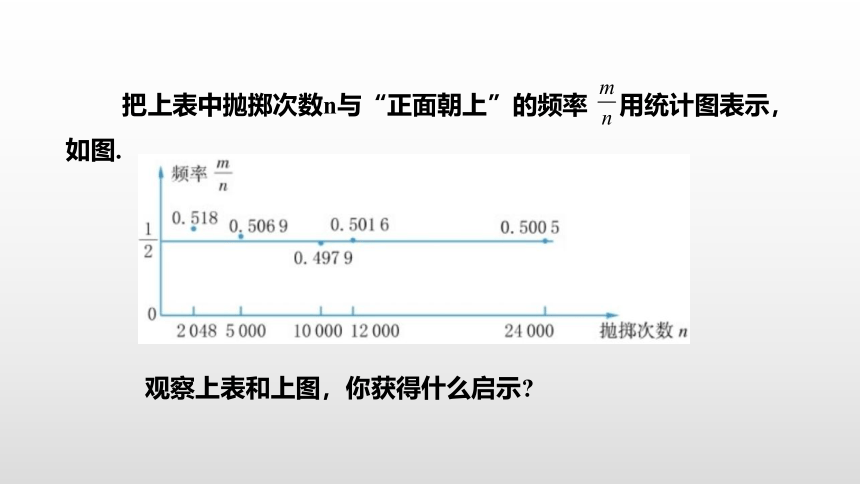
把上表中抛掷次数n与“正面朝上”的频率 用统计图表示,如图.
观察上表和上图,你获得什么启示
让我们来做抛掷两枚硬币的试验.观察它们落地时出现“一正一反”的次数.
1.全班每人各取两枚同样的硬币,做10次掷硬币的试验,填入下表.
学号 试验次数 一正一反的次数 频率
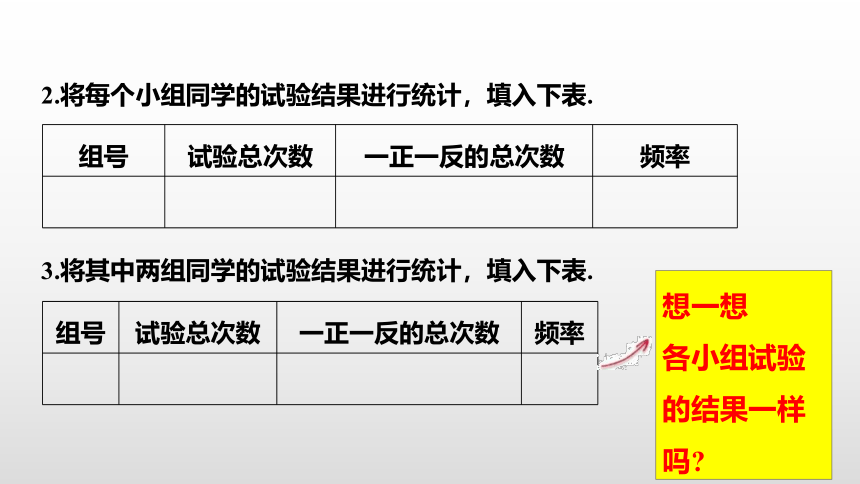
2.将每个小组同学的试验结果进行统计,填入下表.
组号 试验总次数 一正一反的总次数 频率
3.将其中两组同学的试验结果进行统计,填入下表.
组号 试验总次数 一正一反的总次数 频率
想一想
各小组试验的结果一样吗
4.将共甲4组同子的试验结果进何统计,填入类似统表.
5.统计全班同学的试验结果,填入类似统计表.根据上述统计表画出“一正一反”的频率统计图.
议一议:频率与概率有什么区别和联系 随着重复实验次数的增加,频率的变化趋势如何?
频率 概率
区别 试验值或使用时的统计值 理论值
与试验次数的 变化有关 与试验次数的
变化无关
与试验人、试验时间、试验地点有关 与试验人、试验时间、试验地点无关
联系 试验次数越多,频率越趋向于概率 例 在同样条件下对某种小麦种子进行发芽试验,统计发芽种子数,获得如下频数表.
试验种子n(粒) 1 5 50 100 200 500 1000 2000 3000
发芽频数m 0 4 45 92 188 476 951 1900 2850
发芽频率 0
例题讲解
(1)计算上表中的各个频率.
(2)估计该麦种的发芽概率.
(3)如果播种该种小麦每公顷所需麦苗数为4181818棵,种子发芽后的成秧率为87% ,该麦种的千粒质量为35g,那么播种3公顷该种小麦,估计约需麦种多少千克(精确到1 kg)
解 (1)当n=5时,m=4,则发芽的频率 =0.80.依次算得各个频率为0.90,0.92,0.94,0.952,0.951,0.95,0.95.
(2)由第(1)题可知,该麦种的发芽概率约为0.95.
(3)设需麦种x(kg),则粒数为 .由题意,得
×0.95×87%=3×4181818,
解得x≈531(kg).
答:播种3公顷该种小麦,估计约需麦种531 kg.
1.用频率估计概率,可以发现,抛掷硬币“正面朝上”的概率为0.5,是指( )
A.连续抛掷2次,结果一定是“正面朝上”和“反面朝上”各1次
B.连续抛掷100次,结果一定是“正面朝上”和“反面朝上”各50次
C.抛掷2n次硬币,恰好有n次“正面朝上”
D.抛掷n次,当n越来越大时,“正面朝上”的频率会越来越稳定于0.5
D
随堂演练
2.做重复试验:抛掷同一枚啤酒瓶盖1000次.经过统计得“凸面向上”的频率为0.44,则可以由此估计抛掷这枚啤酒瓶盖出现“凹面向上”的概率为( )
A.0.22 B.0.44 C.0.50 D.0.56
D
3.假设抛一枚硬币20次,有8次出现正面,12次出现反面,则出现正面的频率是 ,出现反面的频率是 ,出现正面的概率是 ,出现反面的概率是 .
0.4
0.6
0.5
0.5
4. 某瓷砖厂对最近出炉的一大批某型号瓷砖进行质量抽检,结果如下:
抽取瓷砖数n 100 200 300 400 500 600 800 1000 2000
合格品数m 95 192 287 385 481 577 770 961 1924
合格品率
(1)计算上表中合格品率的各频率(精确到0.001);
(2)估计这种瓷砖的合格品率(精确到0.01);
(3)若该厂本月生产该型号瓷砖500000块,试估计合格品数.
(1)逐项计算,填表如下:
抽取瓷砖数n 100 200 300 400 500 600 800 1000 2000
合格品数m 95 192 287 385 481 577 770 961 1924
合格品率 0.950 0.960 0.957 0.963 0.962 0.962 0.963 0.961 0.962
(2)观察上表,可以发现,当抽取的瓷砖数n≥400时,合格品率 稳定在0.962的附近,
所以我们可取p=0.96作为该型号瓷砖的合格品率的估计.
(3)500000×96%=480000(块),可以估计该型号合格品数为480000块.
解:
思维拓展
某人承包了一池塘养鱼,到了捕捞季他想估计一下收入情况,于是让他读九年级的儿子帮忙.儿子先让他从鱼塘里随意打捞上了60条鱼,把每条鱼都做上标记,放回鱼塘.过了几天,他让父亲从鱼塘内打捞上了50条鱼,结果里面有2条带标记.假设当时这种鱼的市场价为6元/千克,估计平均每条鱼重1.3千克,你能帮助他们估计一下这一池鱼的收入情况吗?
解:设池塘中共有鱼x条,
则 ,解得x=1500.
则池塘中鱼的总质量约为1500×1.3=1950(千克),1950×6=11700(元).
答:这一池鱼的收入约为11700元.
频率与概率的关系
联系: 频率 概率
事件发生的频繁程度
事件发生的
可能性大小
在实际问题中,若事件的概率未知,常用频率的稳定值来估计概率.
区别:频率本身是随机的,在试验前不能确定,做同样次数或不同次数的重复试验得到的事件的频率都可能不同,而概率是一个确定数,是客观存在的,与每次试验无关.
稳定性
大量重复试验
第2章 简单事件的概率
2.3 用频率估计概率
提高运动员的罚球命中率是篮球教练需考虑的问题之一.你认为可以如何估计一位篮球运动员的罚球命中率
问题1 抛掷一枚均匀硬币,硬币落地后,会出现哪些可能的结果呢?
问题2 它们的概率是多少呢?
出现“正面朝上”和“反面朝上”两种情况
都是
问题3 在实际掷硬币时,会出现什么情况呢?
我们知道,任意抛一枚均匀的硬币,”正面朝上”的概率是0.5,许多科学家曾做过成千上万次的实验,其中部分结果如下表:
实验者 抛掷次数n “正面朝上”次数m 频率
隶莫弗 布丰 皮尔逊 皮尔逊 2048 4040 12000 24000 1061 2048 6019 12012 0.518
0.5.69
0.5016
0.5005
获取新知
把上表中抛掷次数n与“正面朝上”的频率 用统计图表示,如图.
观察上表和上图,你获得什么启示
让我们来做抛掷两枚硬币的试验.观察它们落地时出现“一正一反”的次数.
1.全班每人各取两枚同样的硬币,做10次掷硬币的试验,填入下表.
学号 试验次数 一正一反的次数 频率
2.将每个小组同学的试验结果进行统计,填入下表.
组号 试验总次数 一正一反的总次数 频率
3.将其中两组同学的试验结果进行统计,填入下表.
组号 试验总次数 一正一反的总次数 频率
想一想
各小组试验的结果一样吗
4.将共甲4组同子的试验结果进何统计,填入类似统表.
5.统计全班同学的试验结果,填入类似统计表.根据上述统计表画出“一正一反”的频率统计图.
议一议:频率与概率有什么区别和联系 随着重复实验次数的增加,频率的变化趋势如何?
频率 概率
区别 试验值或使用时的统计值 理论值
与试验次数的 变化有关 与试验次数的
变化无关
与试验人、试验时间、试验地点有关 与试验人、试验时间、试验地点无关
联系 试验次数越多,频率越趋向于概率 例 在同样条件下对某种小麦种子进行发芽试验,统计发芽种子数,获得如下频数表.
试验种子n(粒) 1 5 50 100 200 500 1000 2000 3000
发芽频数m 0 4 45 92 188 476 951 1900 2850
发芽频率 0
例题讲解
(1)计算上表中的各个频率.
(2)估计该麦种的发芽概率.
(3)如果播种该种小麦每公顷所需麦苗数为4181818棵,种子发芽后的成秧率为87% ,该麦种的千粒质量为35g,那么播种3公顷该种小麦,估计约需麦种多少千克(精确到1 kg)
解 (1)当n=5时,m=4,则发芽的频率 =0.80.依次算得各个频率为0.90,0.92,0.94,0.952,0.951,0.95,0.95.
(2)由第(1)题可知,该麦种的发芽概率约为0.95.
(3)设需麦种x(kg),则粒数为 .由题意,得
×0.95×87%=3×4181818,
解得x≈531(kg).
答:播种3公顷该种小麦,估计约需麦种531 kg.
1.用频率估计概率,可以发现,抛掷硬币“正面朝上”的概率为0.5,是指( )
A.连续抛掷2次,结果一定是“正面朝上”和“反面朝上”各1次
B.连续抛掷100次,结果一定是“正面朝上”和“反面朝上”各50次
C.抛掷2n次硬币,恰好有n次“正面朝上”
D.抛掷n次,当n越来越大时,“正面朝上”的频率会越来越稳定于0.5
D
随堂演练
2.做重复试验:抛掷同一枚啤酒瓶盖1000次.经过统计得“凸面向上”的频率为0.44,则可以由此估计抛掷这枚啤酒瓶盖出现“凹面向上”的概率为( )
A.0.22 B.0.44 C.0.50 D.0.56
D
3.假设抛一枚硬币20次,有8次出现正面,12次出现反面,则出现正面的频率是 ,出现反面的频率是 ,出现正面的概率是 ,出现反面的概率是 .
0.4
0.6
0.5
0.5
4. 某瓷砖厂对最近出炉的一大批某型号瓷砖进行质量抽检,结果如下:
抽取瓷砖数n 100 200 300 400 500 600 800 1000 2000
合格品数m 95 192 287 385 481 577 770 961 1924
合格品率
(1)计算上表中合格品率的各频率(精确到0.001);
(2)估计这种瓷砖的合格品率(精确到0.01);
(3)若该厂本月生产该型号瓷砖500000块,试估计合格品数.
(1)逐项计算,填表如下:
抽取瓷砖数n 100 200 300 400 500 600 800 1000 2000
合格品数m 95 192 287 385 481 577 770 961 1924
合格品率 0.950 0.960 0.957 0.963 0.962 0.962 0.963 0.961 0.962
(2)观察上表,可以发现,当抽取的瓷砖数n≥400时,合格品率 稳定在0.962的附近,
所以我们可取p=0.96作为该型号瓷砖的合格品率的估计.
(3)500000×96%=480000(块),可以估计该型号合格品数为480000块.
解:
思维拓展
某人承包了一池塘养鱼,到了捕捞季他想估计一下收入情况,于是让他读九年级的儿子帮忙.儿子先让他从鱼塘里随意打捞上了60条鱼,把每条鱼都做上标记,放回鱼塘.过了几天,他让父亲从鱼塘内打捞上了50条鱼,结果里面有2条带标记.假设当时这种鱼的市场价为6元/千克,估计平均每条鱼重1.3千克,你能帮助他们估计一下这一池鱼的收入情况吗?
解:设池塘中共有鱼x条,
则 ,解得x=1500.
则池塘中鱼的总质量约为1500×1.3=1950(千克),1950×6=11700(元).
答:这一池鱼的收入约为11700元.
频率与概率的关系
联系: 频率 概率
事件发生的频繁程度
事件发生的
可能性大小
在实际问题中,若事件的概率未知,常用频率的稳定值来估计概率.
区别:频率本身是随机的,在试验前不能确定,做同样次数或不同次数的重复试验得到的事件的频率都可能不同,而概率是一个确定数,是客观存在的,与每次试验无关.
稳定性
大量重复试验
同课章节目录
