浙教版数学九年级下册同步课件:1.3 第3课时 方位角与仰角、俯角问题(共25张PPT)
文档属性
| 名称 | 浙教版数学九年级下册同步课件:1.3 第3课时 方位角与仰角、俯角问题(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 567.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-12 00:00:00 | ||
图片预览





文档简介
(共25张PPT)
第1章 解直角三角形
1.3 第3课时 方位角与仰角、俯角问题
2.精确度:
边长保留四个有效数字,角度精确到1′.
3.两种情况:
解直角三角形,只有下面两种情况:
(1)已知两条边;
(2)已知一条边和一个锐角
1.解直角三角形.
在直角三角形中,由已知元素求出未知元素的过程,叫做解直角三角形.
实际生活中,如:河道宽度、建筑物测量问题,航空、航海定位问题,均可以用锐角三角函数解决.
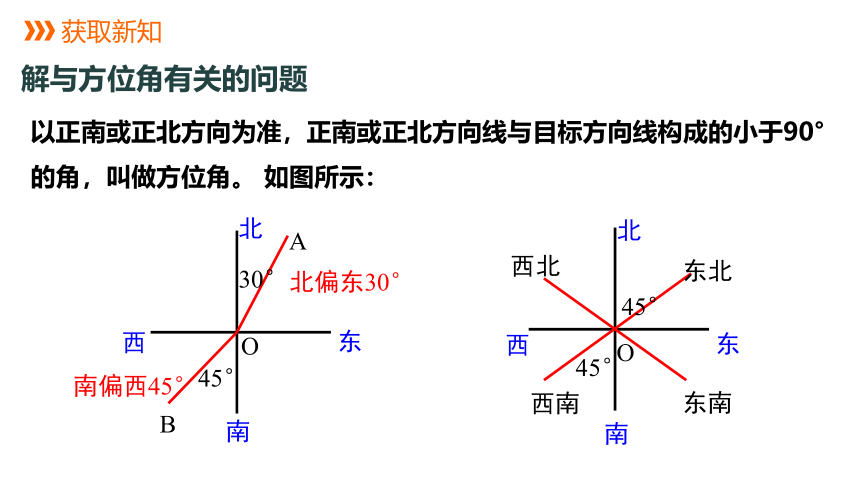
以正南或正北方向为准,正南或正北方向线与目标方向线构成的小于90°的角,叫做方位角。 如图所示:
30°
45°
B
O
A
东
西
北
南
45°
45°
西南
O
东北
东
西
北
南
西北
东南
北偏东30°
南偏西45°
解与方位角有关的问题
获取新知
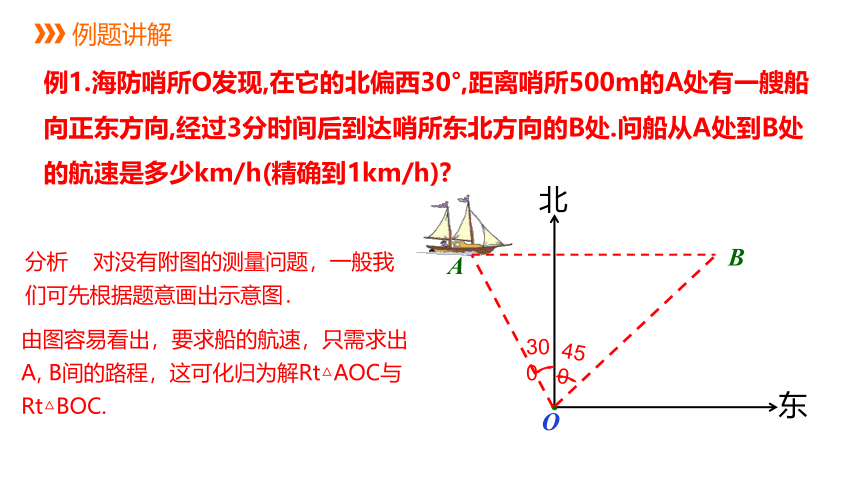
例1.海防哨所O发现,在它的北偏西30°,距离哨所500m的A处有一艘船向正东方向,经过3分时间后到达哨所东北方向的B处.问船从A处到B处的航速是多少km/h(精确到1km/h)
300
北
东
450
O
A
B
例题讲解
分析 对没有附图的测量问题,一般我们可先根据题意画出示意图.
由图容易看出,要求船的航速,只需求出A, B间的路程,这可化归为解Rt△AOC与Rt△BOC.
500
北
东
300
450
O
A
B
C
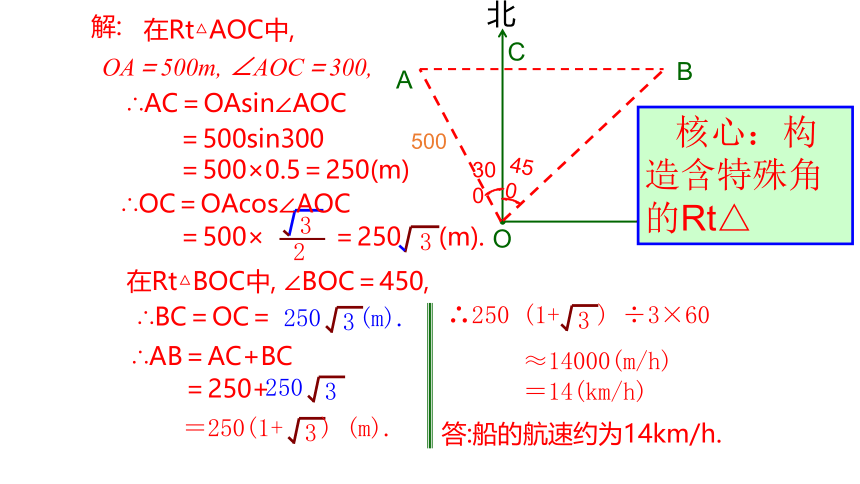
解:
在Rt△AOC中,
OA=500m, ∠AOC=300,
∴AC=OAsin∠AOC
=500sin300
=500× =250 (m).
3
2
3
在Rt△BOC中, ∠BOC=450,
=500×0.5=250(m)
∴OC=OAcos∠AOC
∴BC=OC=
250 (m).
3
∴AB=AC+BC
=250+
250
3
∴250 (1+ ) ÷3×60
3
3
=250(1+ ) (m).
≈14000(m/h)
=14(km/h)
答:船的航速约为14km/h.
核心:构造含特殊角的Rt△
解:过A作AF⊥BC于点F,
则AF的长是A到BC的
最短距离.
∵BD∥CE∥AF,
∴∠DBA=∠BAF=60°,
∠ACE=∠CAF=30°,
∴∠BAC=∠BAF-∠CAF=60°-30°=30°.
例2 如图,海岛A的周围8海里内有暗礁,鱼船跟踪鱼群由西向东航行,在点B处测得海岛A位于北偏东60°,航行12海里到达点C处,又测得海岛A位于北偏东30°,如果鱼船不改变航向继续向东航行.有没有触礁的危险?
北
东
A
C
B
60°
30°
D
E
F
又∵∠ABC =∠DBF-∠DBA
= 90°-60°=30°=∠BAC,
∴BC=AC=12海里,
∴AF=AC · cos30°=6 (海里),
6 ≈10.392>8,
故渔船继续向正东方向行驶,没有触礁的危险.
北
东
A
C
B
60°
30°
D
E
F
如图, 在进行测量时,从下向上看,视线与水平线的夹角叫做仰角;从上往下看,视线与水平线的夹角叫做俯角.
视线
铅垂线
水平线
视线
仰角
俯角
获取新知
解与仰角、俯角有关的问题
例3 如图,直升飞机在长400米的跨江大桥AB的上方P点处,在大桥的两端测得飞机的仰角分别为37°和45 °,求飞机的高度 .(结果取整数. 参考数据:sin37°≈0.8,cos37 °≈0.6,tan 37°≈0.75)
A
B
37°
45°
400米
P
O
解:作PO⊥AB交AB的延长线于O.
设PO=x米,
在Rt△POB中,∠PBO=45°,
OB=PO= x米.
在Rt△POA中,∠PAB=37°,
即
解得x=1200.
故飞机的高度为1200米.
例题讲解
α
β
24m
D
A
C
B
分析:
过D作DE∥BC,
E
问题可转化为解Rt△ABC和Rt△AED.
例4 如图,两建筑物的水平距离BC为24米,从点A测得点D 的俯角a=30°,测得点C 的俯角β=60°,求AB 和CD 两座建筑物的高.(结果保留根号)
F
解:
过D作DE∥BC,则DE⊥AB,
E
在Rt△ABC中,
∠ACB=∠FAC=60°,
∴AB=BC·tan∠ACB
在△ADE中,
∠ADE=∠DAF=30°,
DE=BC=24,
∴AE=DE·tan∠ADE
3
=24·tan30°=8
=24tan60°=24
3
※※※※※※※※※※※※※※※※
∴CD=AB-AE
=24 -8
3
3
=16
3
答:两座建筑物的高分别为24 m和16 m.
3
3
核心:构造含特殊角的Rt△
有关仰角、俯角的实际问题的解决策略:
(1)一般已知两个仰角或两个俯角和一条线段,通过作
垂线段把两个角分别置于两个不同的直角三角形中,
利用锐角三角函数边角关系把要计算的线段和与已
知线段有关的线段的等量关系列出来,借助已知线
段列方程.解方程即可求得.
(2)对于复杂的问题可能会出现两个角两条线段,一般
会通过作辅助线形成矩形和两个直角三角形.
归 纳
随堂演练
1.如图所示,渔船在A处看到灯塔C在北偏东60°方向上,渔船向正东方向航行了12海里到达B处,在B处看到灯塔C在正北方向上,这时渔船与灯塔C的距离是 ( )
A.12海里 B.6海里
C.6海里 D.4海里
B
B
2.如图所示,某飞机于空中A处探测到地平面目标B,此时从飞机上看目标B的俯角α=30°,飞机高度AC=1 200 m,则飞机到目标B的距离AB为 ( )
A.1 200 m B.2 400 m
C.400 m D.1 200 m
3.在一次夏令营活动中,小明同学从营地A出发,要到A地的北偏东60°方向的C处,他先沿正东方向走了200 m到达B地,再沿北偏东30°方向走,恰能到达目的地C(如图),由此可知,B,C两地相距______m.
200
4.如图,在高度是21米的小山A处测得建筑物CD顶部C处的仰角为30°,底部D处的俯角为45°,则这个建筑物的高度CD=____________米.(结果可保留根号)
5.天封塔历史悠久,是宁波著名的文化古迹.如图,从位于天封塔的观测点C测得两建筑物底部A,B的俯角分别为45°和60°,若此观测点离地面的高度为51米,A,B两点在CD的两侧,且点A,D,B在同一水平直线上,求A,B之间的距离.(结果保留根号)
解:由题意得,∠ECA=45°,∠FCB=60°,
∵EF∥AB,
∴∠CAD=∠ECA=45°,∠CBD=∠FCB=60°,
∵∠ADC=∠CDB=90°,
在Rt△CDB中,tan∠CBD= ,
∴BD= tan60° = 51 3 =17 3 ,
∵AD=CD=51米,
∴AB=AD+BD=51+17 3 .
答:A,B之间的距离为(51+17 3 )米.
6.钓鱼岛自古以来就是我国的神圣领土,为维护国家主权和海洋权利,我国海监和渔政部门对钓鱼岛海域实现了常态化巡航管理.如图,某日在我国钓鱼岛附近海域有两艘自西向东航行的海监船A,B,B船在A船的正东方向,且两船保持20海里的距离,某一时刻两海监船同时测得在A的东北方向,B的北偏东15°方向有一我国渔政执法船C,求此时船C与船B的距离是多少.(结果保留根号)
解:作BD⊥AC于点D,
由题意可知,∠BAC=45°,∠ABC=105°,
∴∠ACB=180°-∠BAC-∠ABC=30°,
在Rt△ABD中,
BD=AB·sin∠BAD=20× =10 (海里),
在Rt△BCD中,BC= = =20 (海里),
答:此时船C与船B的距离是20 海里.
仰角、俯
角问题
仰角、俯角的概念
运用解直角三角形解决仰角、俯角问题
解直角三角形的应用
方位角
问题
方位角的概念
运用解直角三角形解决方位角问题
第1章 解直角三角形
1.3 第3课时 方位角与仰角、俯角问题
2.精确度:
边长保留四个有效数字,角度精确到1′.
3.两种情况:
解直角三角形,只有下面两种情况:
(1)已知两条边;
(2)已知一条边和一个锐角
1.解直角三角形.
在直角三角形中,由已知元素求出未知元素的过程,叫做解直角三角形.
实际生活中,如:河道宽度、建筑物测量问题,航空、航海定位问题,均可以用锐角三角函数解决.
以正南或正北方向为准,正南或正北方向线与目标方向线构成的小于90°的角,叫做方位角。 如图所示:
30°
45°
B
O
A
东
西
北
南
45°
45°
西南
O
东北
东
西
北
南
西北
东南
北偏东30°
南偏西45°
解与方位角有关的问题
获取新知
例1.海防哨所O发现,在它的北偏西30°,距离哨所500m的A处有一艘船向正东方向,经过3分时间后到达哨所东北方向的B处.问船从A处到B处的航速是多少km/h(精确到1km/h)
300
北
东
450
O
A
B
例题讲解
分析 对没有附图的测量问题,一般我们可先根据题意画出示意图.
由图容易看出,要求船的航速,只需求出A, B间的路程,这可化归为解Rt△AOC与Rt△BOC.
500
北
东
300
450
O
A
B
C
解:
在Rt△AOC中,
OA=500m, ∠AOC=300,
∴AC=OAsin∠AOC
=500sin300
=500× =250 (m).
3
2
3
在Rt△BOC中, ∠BOC=450,
=500×0.5=250(m)
∴OC=OAcos∠AOC
∴BC=OC=
250 (m).
3
∴AB=AC+BC
=250+
250
3
∴250 (1+ ) ÷3×60
3
3
=250(1+ ) (m).
≈14000(m/h)
=14(km/h)
答:船的航速约为14km/h.
核心:构造含特殊角的Rt△
解:过A作AF⊥BC于点F,
则AF的长是A到BC的
最短距离.
∵BD∥CE∥AF,
∴∠DBA=∠BAF=60°,
∠ACE=∠CAF=30°,
∴∠BAC=∠BAF-∠CAF=60°-30°=30°.
例2 如图,海岛A的周围8海里内有暗礁,鱼船跟踪鱼群由西向东航行,在点B处测得海岛A位于北偏东60°,航行12海里到达点C处,又测得海岛A位于北偏东30°,如果鱼船不改变航向继续向东航行.有没有触礁的危险?
北
东
A
C
B
60°
30°
D
E
F
又∵∠ABC =∠DBF-∠DBA
= 90°-60°=30°=∠BAC,
∴BC=AC=12海里,
∴AF=AC · cos30°=6 (海里),
6 ≈10.392>8,
故渔船继续向正东方向行驶,没有触礁的危险.
北
东
A
C
B
60°
30°
D
E
F
如图, 在进行测量时,从下向上看,视线与水平线的夹角叫做仰角;从上往下看,视线与水平线的夹角叫做俯角.
视线
铅垂线
水平线
视线
仰角
俯角
获取新知
解与仰角、俯角有关的问题
例3 如图,直升飞机在长400米的跨江大桥AB的上方P点处,在大桥的两端测得飞机的仰角分别为37°和45 °,求飞机的高度 .(结果取整数. 参考数据:sin37°≈0.8,cos37 °≈0.6,tan 37°≈0.75)
A
B
37°
45°
400米
P
O
解:作PO⊥AB交AB的延长线于O.
设PO=x米,
在Rt△POB中,∠PBO=45°,
OB=PO= x米.
在Rt△POA中,∠PAB=37°,
即
解得x=1200.
故飞机的高度为1200米.
例题讲解
α
β
24m
D
A
C
B
分析:
过D作DE∥BC,
E
问题可转化为解Rt△ABC和Rt△AED.
例4 如图,两建筑物的水平距离BC为24米,从点A测得点D 的俯角a=30°,测得点C 的俯角β=60°,求AB 和CD 两座建筑物的高.(结果保留根号)
F
解:
过D作DE∥BC,则DE⊥AB,
E
在Rt△ABC中,
∠ACB=∠FAC=60°,
∴AB=BC·tan∠ACB
在△ADE中,
∠ADE=∠DAF=30°,
DE=BC=24,
∴AE=DE·tan∠ADE
3
=24·tan30°=8
=24tan60°=24
3
※※※※※※※※※※※※※※※※
∴CD=AB-AE
=24 -8
3
3
=16
3
答:两座建筑物的高分别为24 m和16 m.
3
3
核心:构造含特殊角的Rt△
有关仰角、俯角的实际问题的解决策略:
(1)一般已知两个仰角或两个俯角和一条线段,通过作
垂线段把两个角分别置于两个不同的直角三角形中,
利用锐角三角函数边角关系把要计算的线段和与已
知线段有关的线段的等量关系列出来,借助已知线
段列方程.解方程即可求得.
(2)对于复杂的问题可能会出现两个角两条线段,一般
会通过作辅助线形成矩形和两个直角三角形.
归 纳
随堂演练
1.如图所示,渔船在A处看到灯塔C在北偏东60°方向上,渔船向正东方向航行了12海里到达B处,在B处看到灯塔C在正北方向上,这时渔船与灯塔C的距离是 ( )
A.12海里 B.6海里
C.6海里 D.4海里
B
B
2.如图所示,某飞机于空中A处探测到地平面目标B,此时从飞机上看目标B的俯角α=30°,飞机高度AC=1 200 m,则飞机到目标B的距离AB为 ( )
A.1 200 m B.2 400 m
C.400 m D.1 200 m
3.在一次夏令营活动中,小明同学从营地A出发,要到A地的北偏东60°方向的C处,他先沿正东方向走了200 m到达B地,再沿北偏东30°方向走,恰能到达目的地C(如图),由此可知,B,C两地相距______m.
200
4.如图,在高度是21米的小山A处测得建筑物CD顶部C处的仰角为30°,底部D处的俯角为45°,则这个建筑物的高度CD=____________米.(结果可保留根号)
5.天封塔历史悠久,是宁波著名的文化古迹.如图,从位于天封塔的观测点C测得两建筑物底部A,B的俯角分别为45°和60°,若此观测点离地面的高度为51米,A,B两点在CD的两侧,且点A,D,B在同一水平直线上,求A,B之间的距离.(结果保留根号)
解:由题意得,∠ECA=45°,∠FCB=60°,
∵EF∥AB,
∴∠CAD=∠ECA=45°,∠CBD=∠FCB=60°,
∵∠ADC=∠CDB=90°,
在Rt△CDB中,tan∠CBD= ,
∴BD= tan60° = 51 3 =17 3 ,
∵AD=CD=51米,
∴AB=AD+BD=51+17 3 .
答:A,B之间的距离为(51+17 3 )米.
6.钓鱼岛自古以来就是我国的神圣领土,为维护国家主权和海洋权利,我国海监和渔政部门对钓鱼岛海域实现了常态化巡航管理.如图,某日在我国钓鱼岛附近海域有两艘自西向东航行的海监船A,B,B船在A船的正东方向,且两船保持20海里的距离,某一时刻两海监船同时测得在A的东北方向,B的北偏东15°方向有一我国渔政执法船C,求此时船C与船B的距离是多少.(结果保留根号)
解:作BD⊥AC于点D,
由题意可知,∠BAC=45°,∠ABC=105°,
∴∠ACB=180°-∠BAC-∠ABC=30°,
在Rt△ABD中,
BD=AB·sin∠BAD=20× =10 (海里),
在Rt△BCD中,BC= = =20 (海里),
答:此时船C与船B的距离是20 海里.
仰角、俯
角问题
仰角、俯角的概念
运用解直角三角形解决仰角、俯角问题
解直角三角形的应用
方位角
问题
方位角的概念
运用解直角三角形解决方位角问题
