浙教版九年级下册2.3 三角形的内切圆(共18张PPT)
文档属性
| 名称 | 浙教版九年级下册2.3 三角形的内切圆(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 270.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-12 00:00:00 | ||
图片预览



文档简介
(共18张PPT)
第2章 直线与圆的位置关系
2.3 三角形的内切圆
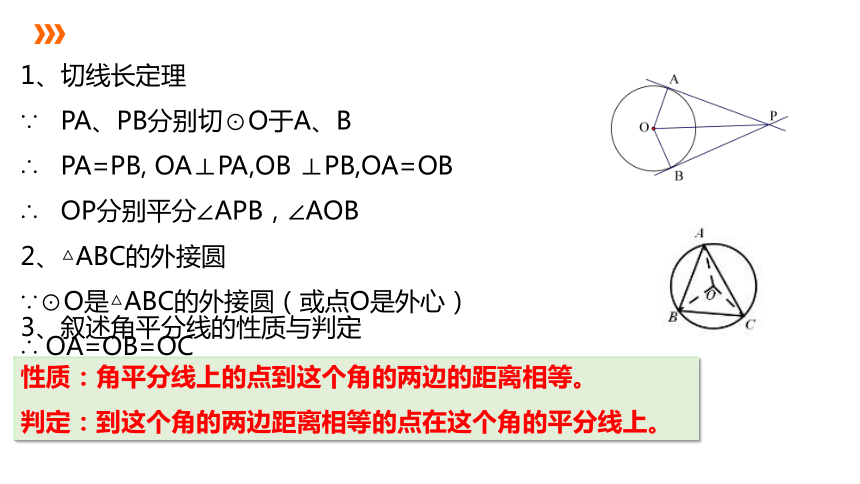
1、切线长定理
∵ PA、PB分别切⊙O于A、B
∴ PA=PB, OA⊥PA,OB ⊥PB,OA=OB
∴ OP分别平分∠APB,∠AOB
2、△ABC的外接圆
∵⊙O是△ABC的外接圆(或点O是外心)
∴ OA=OB=OC
3、叙述角平分线的性质与判定
性质:角平分线上的点到这个角的两边的距离相等。
判定:到这个角的两边距离相等的点在这个角的平分线上。
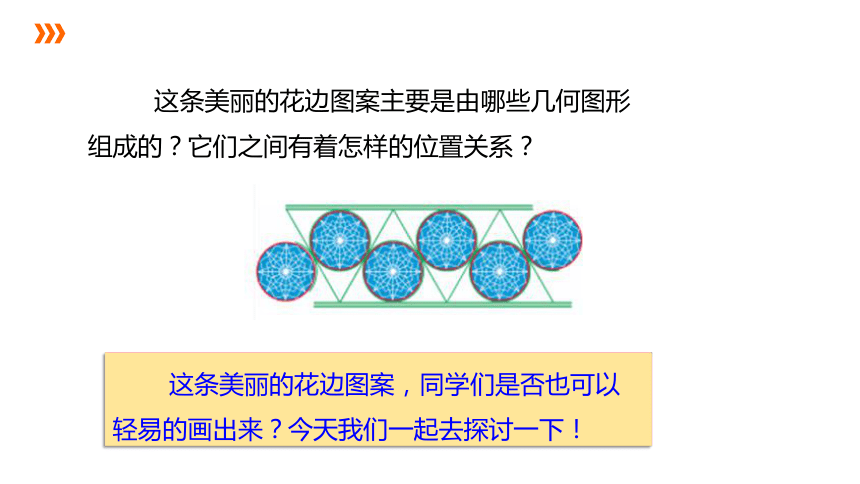
这条美丽的花边图案主要是由哪些几何图形组成的?它们之间有着怎样的位置关系?
这条美丽的花边图案,同学们是否也可以轻易的画出来?今天我们一起去探讨一下!
小明在一家木料厂上班,工作之余想对厂里的三角形废料进行加工:裁下一块圆形用料,怎样才能使裁下的圆的面积尽可能大呢?
一起探究
获取新知
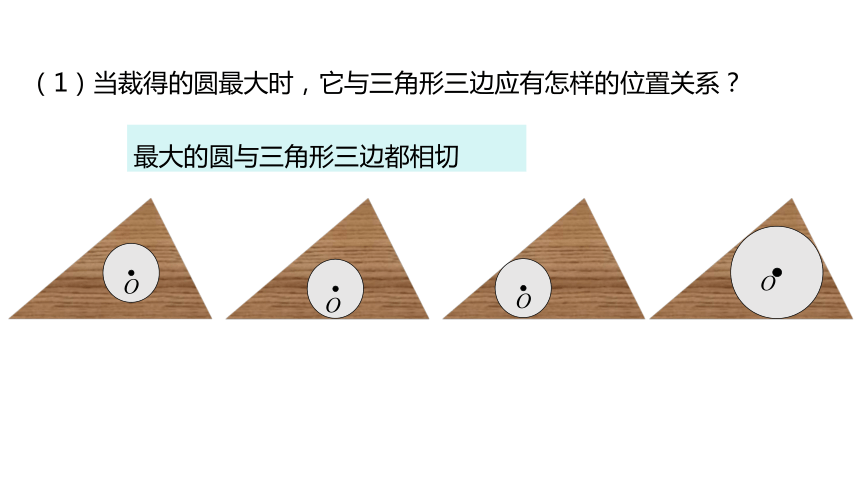
(1)当裁得的圆最大时,它与三角形三边应有怎样的位置关系?
O
O
O
O
最大的圆与三角形三边都相切
作出三个内角的平分线,三条内角平分线相交于一点,这点就是圆心,
O
C
A
B
D
(2)与三角形的一个角的两边都相切的圆的圆心在哪里?
(3)如何确定这个圆的圆心位置与半径的长?
过圆心作一边的垂线,垂线段的长就是半径。
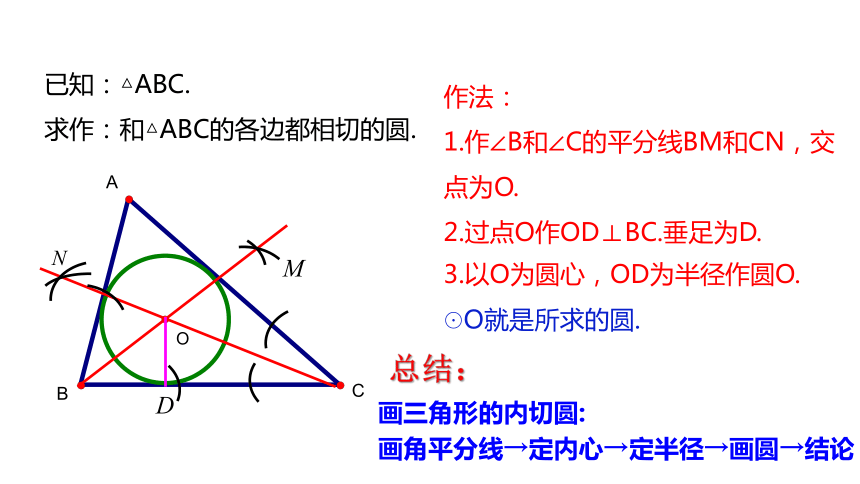
已知:△ABC.
求作:和△ABC的各边都相切的圆.
M
N
D
作法:
1.作∠B和∠C的平分线BM和CN,交点为O.
2.过点O作OD⊥BC.垂足为D.
☉O就是所求的圆.
3.以O为圆心,OD为半径作圆O.
总结:
画三角形的内切圆:
画角平分线→定内心→定半径→画圆→结论
2.三角形内切圆的圆心叫做这个三角形的内心.
3.这个三角形叫做这个圆的外切三角形.
B
A
C
I
☉I是△ABC的内切圆,点I是△ABC的内心,△ABC是☉I的外切三角形.
1.与三角形三边都相切的圆叫作三角形的内切圆.
知识总结
1.三角形的内心到三角形各边的距离相等。
三角形的内心性质
C
B
A
D
F
E
O
r
2.三角形的内心在三角形的角平分线上。
拓 展
OA,OB,OC是△ABC的角平分线,OD=OE=OF.
内心、外心的区别与联系
名称 内心 外心
图形
由来 三角形三条角平分线的交点 三角形三边垂直平分线的交点
性质 到三角形三边的距离相等 到三角形三个顶点的距离相等
位置 一定在三角形内部 不一定在三角形内部
角度关系 ∠BOC=90°+ ∠A ∠BIC=2∠A
比 较
例1 如图,等边三角形ABC的边长为3 cm,求△ABC的内切圆⊙O的半径.
如图,设⊙O切AB于点D,连结OA,OB,OD.
∵ ⊙O是△ABC的内切圆,
∴AO,BO 是∠BAC, ∠ABC的角平分线.
∵△ABC是等边三角形,
∴∠OAB=∠OBA = 30°.
解:
例题讲解
∵OD⊥AB,AB=3cm,
∴AD=BD= AB=1.5(cm),
∴OD=AD×tan30°
答:△ABC的内切圆的半径为
例2 已知:如图, ⊙O是△ABC的内切圆,切点分别为D,E,F.设△ABC的周长为l,求证: AE+BC= l.
∵⊙O是△ABC的内切圆,E,F为切点,
∴AE=AF.
同理,BD=BF,CD=CE.
∴AE+BC=AE+BD+CD
= (AE+AF+BD+BF+CD+CE)
=
证明:
1.如图,已知点O是△ABC 的内心,且∠ABC= 60 °, ∠ACB= 80 °,则∠BOC= .
A
B
C
O
110 °
随堂演练
(3)若∠BIC=100 °,则∠A = 度.
(2)若∠A=80 °,则∠BIC = 度.
130
20
2.如图,在△ABC中,点I是内心,
(1)若∠ABC=50°, ∠ACB=70°,∠BIC=_____.
A
B
C
I
(4)试探索: ∠A与∠BIC之间存在怎样的数量关系?
120°
3. △ABC的内切圆☉O与BC、CA、AB分别相切于点D、E、F,且AB=13cm,BC=14cm,CA=9cm,求AF、BD、CE的长.
B
A
C
E
D
F
O
解:
设AF=xcm,则AE=xcm.
∴CE=CD=AC-AE=9-x(cm),
BF=BD=AB-AF=13-x(cm).
由 BD+CD=BC,可得
(13-x)+(9-x)=14,
解得 x=4.
∴ AF=4(cm),BD=9(cm),CE=5(cm).
4.如图,△ABC中,I是内心,∠A的平分线和△ABC的外接圆相交于点D.
求证:DI=DB.
证明:连接BI.
∵I是△ABC的内心,
∴∠BAD=∠CAD,∠ABI=∠CBI,
∵∠CBD=∠CAD,
∴∠BAD=∠CBD,
∵∠BID=∠BAD+∠ABI,∠IBD=∠CBI+∠CBD,
∴∠BID=∠IBD,
∴BD=ID.
名称 确定方法 图形 性质
内心:三角形内切圆的圆心
三角形三条
角平分线的
交点
1.到三边的距离相等;
2.OA、OB、OC分别平分∠BAC、∠ABC、∠ACB
3.内心在三角形内部.
A
B
C
O
第2章 直线与圆的位置关系
2.3 三角形的内切圆
1、切线长定理
∵ PA、PB分别切⊙O于A、B
∴ PA=PB, OA⊥PA,OB ⊥PB,OA=OB
∴ OP分别平分∠APB,∠AOB
2、△ABC的外接圆
∵⊙O是△ABC的外接圆(或点O是外心)
∴ OA=OB=OC
3、叙述角平分线的性质与判定
性质:角平分线上的点到这个角的两边的距离相等。
判定:到这个角的两边距离相等的点在这个角的平分线上。
这条美丽的花边图案主要是由哪些几何图形组成的?它们之间有着怎样的位置关系?
这条美丽的花边图案,同学们是否也可以轻易的画出来?今天我们一起去探讨一下!
小明在一家木料厂上班,工作之余想对厂里的三角形废料进行加工:裁下一块圆形用料,怎样才能使裁下的圆的面积尽可能大呢?
一起探究
获取新知
(1)当裁得的圆最大时,它与三角形三边应有怎样的位置关系?
O
O
O
O
最大的圆与三角形三边都相切
作出三个内角的平分线,三条内角平分线相交于一点,这点就是圆心,
O
C
A
B
D
(2)与三角形的一个角的两边都相切的圆的圆心在哪里?
(3)如何确定这个圆的圆心位置与半径的长?
过圆心作一边的垂线,垂线段的长就是半径。
已知:△ABC.
求作:和△ABC的各边都相切的圆.
M
N
D
作法:
1.作∠B和∠C的平分线BM和CN,交点为O.
2.过点O作OD⊥BC.垂足为D.
☉O就是所求的圆.
3.以O为圆心,OD为半径作圆O.
总结:
画三角形的内切圆:
画角平分线→定内心→定半径→画圆→结论
2.三角形内切圆的圆心叫做这个三角形的内心.
3.这个三角形叫做这个圆的外切三角形.
B
A
C
I
☉I是△ABC的内切圆,点I是△ABC的内心,△ABC是☉I的外切三角形.
1.与三角形三边都相切的圆叫作三角形的内切圆.
知识总结
1.三角形的内心到三角形各边的距离相等。
三角形的内心性质
C
B
A
D
F
E
O
r
2.三角形的内心在三角形的角平分线上。
拓 展
OA,OB,OC是△ABC的角平分线,OD=OE=OF.
内心、外心的区别与联系
名称 内心 外心
图形
由来 三角形三条角平分线的交点 三角形三边垂直平分线的交点
性质 到三角形三边的距离相等 到三角形三个顶点的距离相等
位置 一定在三角形内部 不一定在三角形内部
角度关系 ∠BOC=90°+ ∠A ∠BIC=2∠A
比 较
例1 如图,等边三角形ABC的边长为3 cm,求△ABC的内切圆⊙O的半径.
如图,设⊙O切AB于点D,连结OA,OB,OD.
∵ ⊙O是△ABC的内切圆,
∴AO,BO 是∠BAC, ∠ABC的角平分线.
∵△ABC是等边三角形,
∴∠OAB=∠OBA = 30°.
解:
例题讲解
∵OD⊥AB,AB=3cm,
∴AD=BD= AB=1.5(cm),
∴OD=AD×tan30°
答:△ABC的内切圆的半径为
例2 已知:如图, ⊙O是△ABC的内切圆,切点分别为D,E,F.设△ABC的周长为l,求证: AE+BC= l.
∵⊙O是△ABC的内切圆,E,F为切点,
∴AE=AF.
同理,BD=BF,CD=CE.
∴AE+BC=AE+BD+CD
= (AE+AF+BD+BF+CD+CE)
=
证明:
1.如图,已知点O是△ABC 的内心,且∠ABC= 60 °, ∠ACB= 80 °,则∠BOC= .
A
B
C
O
110 °
随堂演练
(3)若∠BIC=100 °,则∠A = 度.
(2)若∠A=80 °,则∠BIC = 度.
130
20
2.如图,在△ABC中,点I是内心,
(1)若∠ABC=50°, ∠ACB=70°,∠BIC=_____.
A
B
C
I
(4)试探索: ∠A与∠BIC之间存在怎样的数量关系?
120°
3. △ABC的内切圆☉O与BC、CA、AB分别相切于点D、E、F,且AB=13cm,BC=14cm,CA=9cm,求AF、BD、CE的长.
B
A
C
E
D
F
O
解:
设AF=xcm,则AE=xcm.
∴CE=CD=AC-AE=9-x(cm),
BF=BD=AB-AF=13-x(cm).
由 BD+CD=BC,可得
(13-x)+(9-x)=14,
解得 x=4.
∴ AF=4(cm),BD=9(cm),CE=5(cm).
4.如图,△ABC中,I是内心,∠A的平分线和△ABC的外接圆相交于点D.
求证:DI=DB.
证明:连接BI.
∵I是△ABC的内心,
∴∠BAD=∠CAD,∠ABI=∠CBI,
∵∠CBD=∠CAD,
∴∠BAD=∠CBD,
∵∠BID=∠BAD+∠ABI,∠IBD=∠CBI+∠CBD,
∴∠BID=∠IBD,
∴BD=ID.
名称 确定方法 图形 性质
内心:三角形内切圆的圆心
三角形三条
角平分线的
交点
1.到三边的距离相等;
2.OA、OB、OC分别平分∠BAC、∠ABC、∠ACB
3.内心在三角形内部.
A
B
C
O
