浙教版数学九年级上册同步课件:3.3 第2课时 垂径定理的逆定理(共15张PPT)
文档属性
| 名称 | 浙教版数学九年级上册同步课件:3.3 第2课时 垂径定理的逆定理(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 898.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-12 22:06:01 | ||
图片预览




文档简介
(共15张PPT)
第3章圆的基本性质
3.3 第2课时 垂径定理的逆定理
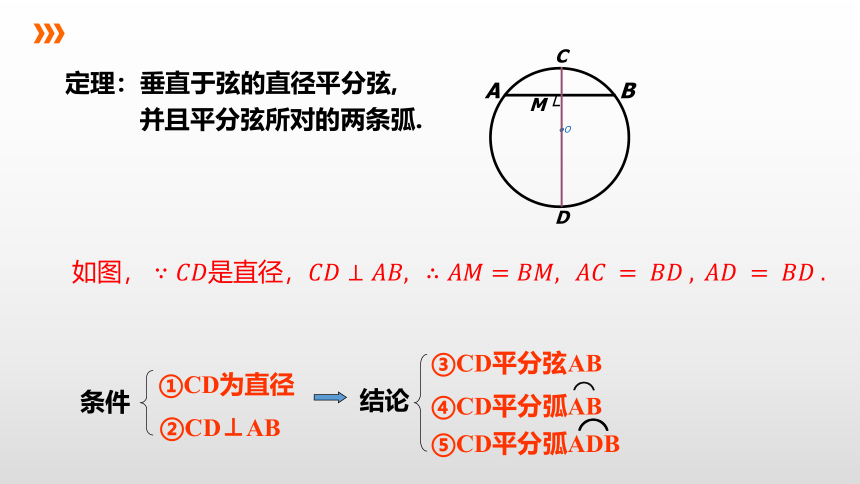
定理:垂直于弦的直径平分弦,
并且平分弦所对的两条弧.
●O
A
B
C
D
M└
条件
①CD为直径
②CD⊥AB
⑤CD平分弧ADB
③CD平分弦AB
④CD平分弧AB
结论
⌒
⌒
学习目标
1.掌握垂径定理的逆定理.
2.会运用垂径定理的逆定理解决一些简单的几何问题.
垂径定理的逆命题是什么?
垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧.
逆命题1:平分弦的直径垂直于弦。
逆命题2:平分弧的直径垂直于弧所对的弦。
条件
结论1
结论2
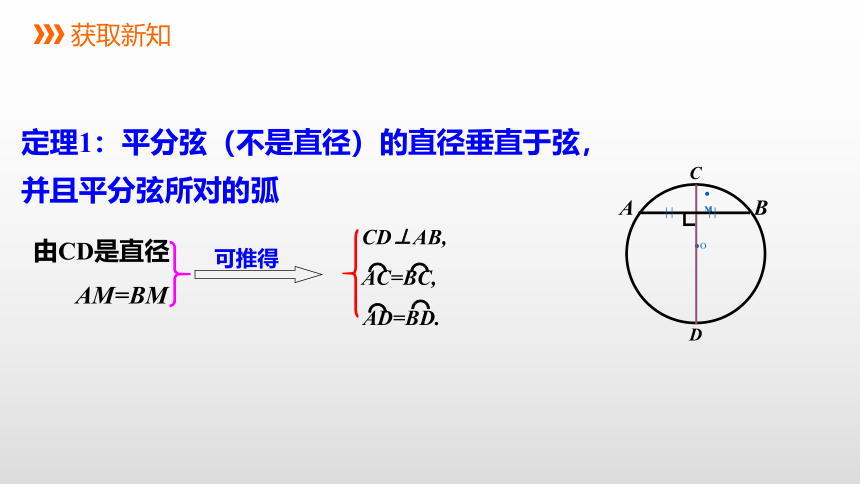
定理1:平分弦(不是直径)的直径垂直于弦, 并且平分弦所对的弧
由CD是直径
AM=BM
可推得
⌒
⌒
AC=BC,
⌒
⌒
AD=BD.
CD⊥AB,
●O
C
D
●
M
A
B
┗
获取新知
.
O
A
E
B
D
C
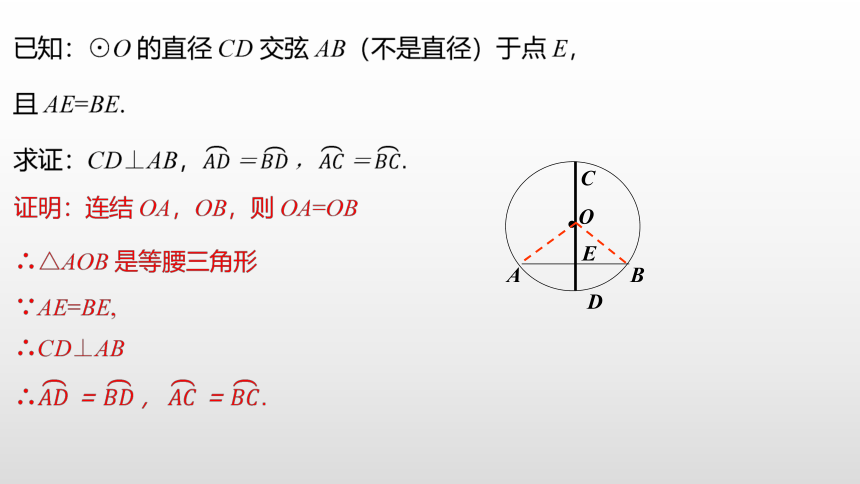
定理2:平分弧的直径垂直平分弧所对的弦
由CD是直径
AM=BM
可推得
⌒
⌒
AC=BC,
⌒
⌒
AD=BD.
CD⊥AB,
当AC=BC时,将图形沿直径CD所在的直线对折,则AC与BC重合.所以点A与点B重合,即A,B关于直线CD对称,所以CD垂直平分弦AB,这就证明了定理2.
⌒
例 赵州桥(如图)是我国隋代建造的石拱桥,距今约有1400年的历史,是我国古代人民勤劳与智慧的结晶.它的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为37.02 m,拱高(弧的中点到弦的距离)为7.23 m,求赵州桥主桥拱的半径(结果保留小数点后一位).
例题讲解
总结:运用垂径定理的逆定理解决一些简单的几何问题.
1.有下列四个条件:①经过圆心;②垂直于弦;③平分弦;④平分弦所对的弧.由上述四个条件组成的命题中,是假命题的是( )
A.①② ③④ B.①③ ②④
C.①④ ②③ D.②③ ①④
D
随堂演练
2.如图,一条公路弯道处是一段圆弧AB,点O是这条弧所在圆的圆心,C是的中点,OC与AB相交于点D.已知AB=120 m,CD=20 m,那么这段弯道所在圆的半径为( )
C
思维拓展
垂直
垂直于弦
平分
平分
第3章圆的基本性质
3.3 第2课时 垂径定理的逆定理
定理:垂直于弦的直径平分弦,
并且平分弦所对的两条弧.
●O
A
B
C
D
M└
条件
①CD为直径
②CD⊥AB
⑤CD平分弧ADB
③CD平分弦AB
④CD平分弧AB
结论
⌒
⌒
学习目标
1.掌握垂径定理的逆定理.
2.会运用垂径定理的逆定理解决一些简单的几何问题.
垂径定理的逆命题是什么?
垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧.
逆命题1:平分弦的直径垂直于弦。
逆命题2:平分弧的直径垂直于弧所对的弦。
条件
结论1
结论2
定理1:平分弦(不是直径)的直径垂直于弦, 并且平分弦所对的弧
由CD是直径
AM=BM
可推得
⌒
⌒
AC=BC,
⌒
⌒
AD=BD.
CD⊥AB,
●O
C
D
●
M
A
B
┗
获取新知
.
O
A
E
B
D
C
定理2:平分弧的直径垂直平分弧所对的弦
由CD是直径
AM=BM
可推得
⌒
⌒
AC=BC,
⌒
⌒
AD=BD.
CD⊥AB,
当AC=BC时,将图形沿直径CD所在的直线对折,则AC与BC重合.所以点A与点B重合,即A,B关于直线CD对称,所以CD垂直平分弦AB,这就证明了定理2.
⌒
例 赵州桥(如图)是我国隋代建造的石拱桥,距今约有1400年的历史,是我国古代人民勤劳与智慧的结晶.它的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为37.02 m,拱高(弧的中点到弦的距离)为7.23 m,求赵州桥主桥拱的半径(结果保留小数点后一位).
例题讲解
总结:运用垂径定理的逆定理解决一些简单的几何问题.
1.有下列四个条件:①经过圆心;②垂直于弦;③平分弦;④平分弦所对的弧.由上述四个条件组成的命题中,是假命题的是( )
A.①② ③④ B.①③ ②④
C.①④ ②③ D.②③ ①④
D
随堂演练
2.如图,一条公路弯道处是一段圆弧AB,点O是这条弧所在圆的圆心,C是的中点,OC与AB相交于点D.已知AB=120 m,CD=20 m,那么这段弯道所在圆的半径为( )
C
思维拓展
垂直
垂直于弦
平分
平分
同课章节目录
