浙教版数学九年级上册:4.4 第1课时 三角形相似的预备定理和判定定理1(利用两角关系) 同步课件(22张ppt)
文档属性
| 名称 | 浙教版数学九年级上册:4.4 第1课时 三角形相似的预备定理和判定定理1(利用两角关系) 同步课件(22张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1014.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-13 07:47:57 | ||
图片预览







文档简介
(共22张PPT)
第4章 相似三角形
4.4 第1课时 三角形相似的预备定理
和判定定理1(利用两角关系)
如何测量河的宽度?
学习目标
1.掌握三角形的相似判定的预备定理,
了解它的证明过程.
2.掌握三角形相似的判定定理1,并能
运用这个定理证明两个三角形相似.
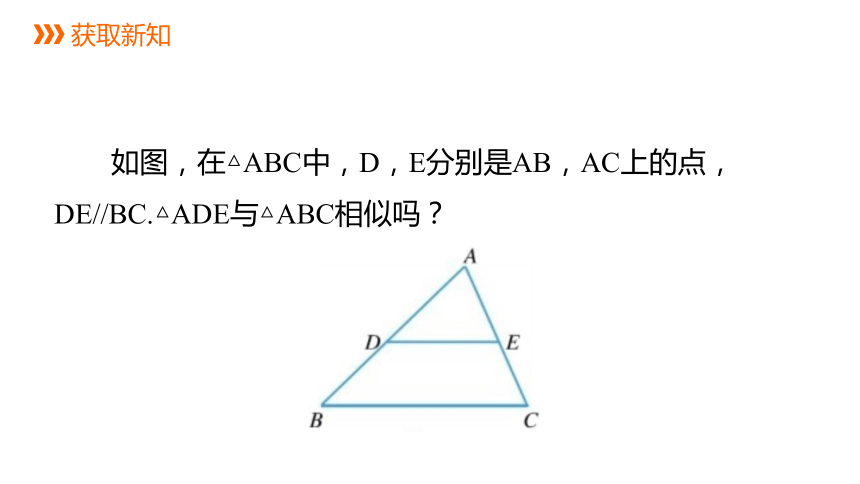
如图,在△ABC中,D,E分别是AB,AC上的点,DE//BC.△ADE与△ABC相似吗?
获取新知
平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
1.判定三角形相似的预备定理
回顾判定两个三角形全等的条件,猜想相应的有哪些判定两个三角形相似的条件.
根据三角形相似的预备定理,我们可以得到以下三角形相似的判定定理:
有两个角对应相等的两个三角形相似.
2.判定三角形相似的定理1
下面给出证明.
已知:如图,在△ABC与△A'B'C'中,∠A=∠A',∠B=∠B'.
求证:△ABC∽△A'B'C'.
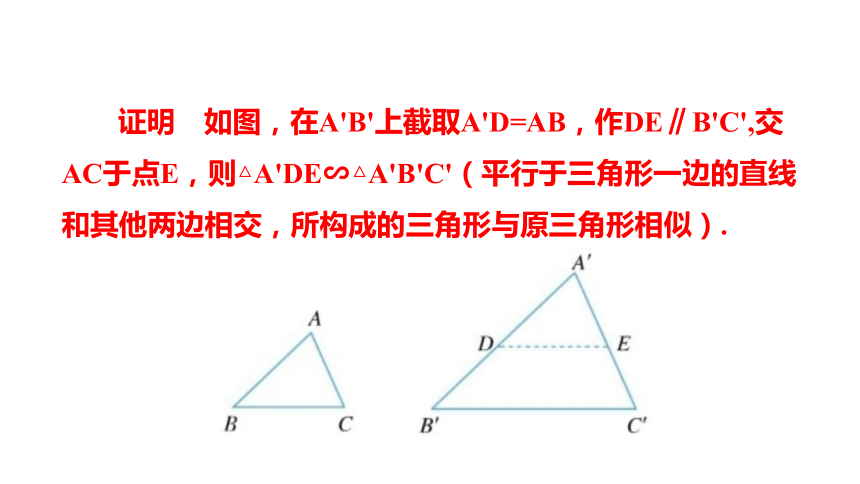
证明 如图,在A'B'上截取A'D=AB,作DE∥B'C',交AC于点E,则△A'DE∽△A'B'C'(平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似).
又∵∠A=∠A',∠B=∠B'=∠A'DE,
∴△ABC≌△A'DE,
∴△ABC∽△A'B'C'.
例1 在一次数学活动课上,为了测量河宽AB,小聪采用了如下方法(如图):
例题讲解
从A处沿与AB垂直的直线方向走45 m到达C处,插一根标杆,然后沿同方向继续走15m到达D处,再右转90°走到E处,使B,C,E三点恰好在一条直线上.量得DE=20 m,这样就可以求出河宽AB.请你说明理由,
并算出结果.
解 ∵AB⊥AD,DE⊥AD,
∴∠BAC=∠EDC=Rt∠.
又∵∠ACB=∠DCE,
∴△ABC∽△DEC(有两个
角对应相等的两个三角形相似),
∴ = .
∵ AC=45,CD=15,DE=20,
∴ = ,
∴ AB= =60(m).
答:河宽AB是60 m.
【归纳总结】利用预备定理和判定定理1判定两个三角形相似的基本模型:(1)用预备定理判定相似有两种基本图形(如图①②,其中DE∥BC):“A”字形相似(图①),“X”字形相似(图②);
(2)用判定定理1判定相似有三种基本图形(如图③④⑤):“Y”字形相似(如图③,其中∠CDE=∠A;如图④,其中∠CDA=∠CAB),“W”字形相似(如图⑤,其中∠B=∠E).
B
随堂演练
2.如图,P是 ABCD的边AB上的一点,射线CP交DA的延长线于点E,则图中相似的三角形有( )
A.0对 B.1对
C.2对 D.3对
D
两个角
第4章 相似三角形
4.4 第1课时 三角形相似的预备定理
和判定定理1(利用两角关系)
如何测量河的宽度?
学习目标
1.掌握三角形的相似判定的预备定理,
了解它的证明过程.
2.掌握三角形相似的判定定理1,并能
运用这个定理证明两个三角形相似.
如图,在△ABC中,D,E分别是AB,AC上的点,DE//BC.△ADE与△ABC相似吗?
获取新知
平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
1.判定三角形相似的预备定理
回顾判定两个三角形全等的条件,猜想相应的有哪些判定两个三角形相似的条件.
根据三角形相似的预备定理,我们可以得到以下三角形相似的判定定理:
有两个角对应相等的两个三角形相似.
2.判定三角形相似的定理1
下面给出证明.
已知:如图,在△ABC与△A'B'C'中,∠A=∠A',∠B=∠B'.
求证:△ABC∽△A'B'C'.
证明 如图,在A'B'上截取A'D=AB,作DE∥B'C',交AC于点E,则△A'DE∽△A'B'C'(平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似).
又∵∠A=∠A',∠B=∠B'=∠A'DE,
∴△ABC≌△A'DE,
∴△ABC∽△A'B'C'.
例1 在一次数学活动课上,为了测量河宽AB,小聪采用了如下方法(如图):
例题讲解
从A处沿与AB垂直的直线方向走45 m到达C处,插一根标杆,然后沿同方向继续走15m到达D处,再右转90°走到E处,使B,C,E三点恰好在一条直线上.量得DE=20 m,这样就可以求出河宽AB.请你说明理由,
并算出结果.
解 ∵AB⊥AD,DE⊥AD,
∴∠BAC=∠EDC=Rt∠.
又∵∠ACB=∠DCE,
∴△ABC∽△DEC(有两个
角对应相等的两个三角形相似),
∴ = .
∵ AC=45,CD=15,DE=20,
∴ = ,
∴ AB= =60(m).
答:河宽AB是60 m.
【归纳总结】利用预备定理和判定定理1判定两个三角形相似的基本模型:(1)用预备定理判定相似有两种基本图形(如图①②,其中DE∥BC):“A”字形相似(图①),“X”字形相似(图②);
(2)用判定定理1判定相似有三种基本图形(如图③④⑤):“Y”字形相似(如图③,其中∠CDE=∠A;如图④,其中∠CDA=∠CAB),“W”字形相似(如图⑤,其中∠B=∠E).
B
随堂演练
2.如图,P是 ABCD的边AB上的一点,射线CP交DA的延长线于点E,则图中相似的三角形有( )
A.0对 B.1对
C.2对 D.3对
D
两个角
同课章节目录
