浙教版数学九年级上册同步课件:3.4 第1课时 圆心角定理(共21张PPT)
文档属性
| 名称 | 浙教版数学九年级上册同步课件:3.4 第1课时 圆心角定理(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-12 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
第3章圆的基本性质
3.4 第1课时 圆心角
熊宝宝要过生日了!要把蛋糕平均分成四块,你会分吗?
学习目标
1.经历形成圆的概念的过程,经历探索点与圆
的位置关系的过程.
2.理解圆的概念,用符号、字母正确表示弦和
弧,了解点与圆的位置关系.
3.会在简单条件下判断点与圆的位置关系.
结论:圆是中心对称图形
观察:1.将圆绕圆心旋转180°后,得到的图形与原图形重合吗?由此你得到什么结论呢?
.
O
A
B
180°
获取新知
1.对称性
将圆沿直径所在直线对折,你发现了什么?这就说明圆还是什么图形?
把圆绕圆心旋转任意一个角度呢?仍与原来的圆重合吗?
O
α
结论:圆是旋转对称图形,具有旋转不变性
·
2.旋转不变性
顶点在圆心的角叫做圆心角(central angle).
注意:
1.顶点在圆心;
2.端点在圆上
必须同时满足
例如,如图中,∠NON'就是一个圆心角.
3.圆心角的定义
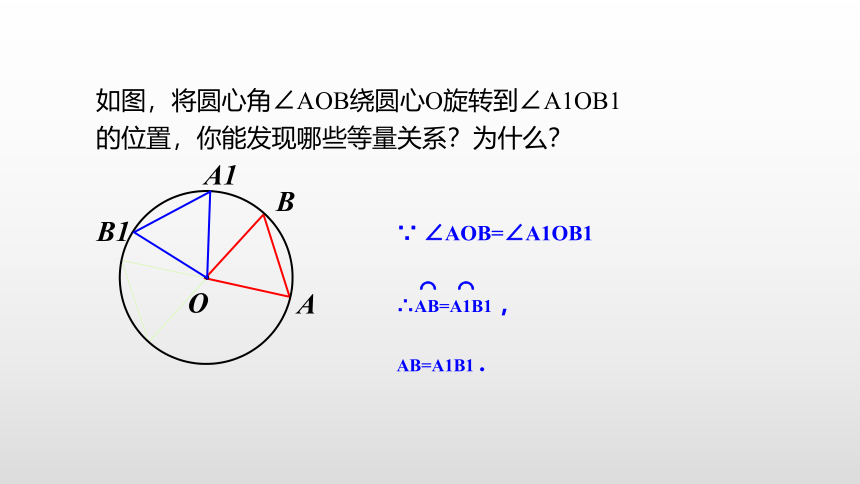
如图,将圆心角∠AOB绕圆心O旋转到∠A1OB1的位置,你能发现哪些等量关系?为什么?
∵ ∠AOB=∠A1OB1
∴AB=A1B1 ,
AB=A1B1 .
⌒
⌒
·
O
A
B
A1
B1
如图,⊙O与⊙O1是等圆,∠AOB =∠A1OB1=60°,
请问上述结论还成立吗?为什么
·
O
A
B
A1
·
O1
B1
·
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.
①∠AOB=∠COD
②AB=CD
⌒ ⌒
③AB=CD
A
B
O
D
C
4.圆心角定理
如果以⊙O的圆心O为端点作360条射线,把以O为顶点的周角360等分,那么根据圆心角定理,这些射线也把圆360等分.
⌒
每相邻两条射线所成的圆心角是1°的角,
我们把1 °圆心角所对的弧叫做1°的弧.
这样,n°的圆心角所对的弧就
是n°的弧(如图).
5.弧的度数
例1 用直尺和圆规把⊙O(如图)四等分.
例题讲解
作法 如图.
1.作⊙O的一条直径AB.
2.过点O作CD⊥AB,交⊙O于点
C和点D.
点A,B,C,D就把⊙O四等分.
结论:互相垂直的直径,将圆四等分.
例2 求证:在同圆或等圆中,相等的圆心角所对两条弦的弦心距相等.已知:如图,在⊙O中,∠AOB=∠COD,OE是弦AB的弦心距,
OF是弦CD的弦心距.
求证:OE=OF.
证明:∵∠AOB=∠COD,
∴AB=CD(圆心角定理).
∴OE⊥AB,
AE=BE= 1/2 AB(根据什么?).
同理,由OF⊥DC,得DF=CF= 1/2 CD.
∴AE=DF.
又∵OA=OD,
∴Rt△AOE≌Rt△DOF,∴OE=OF.
识记:在同圆或等圆中,相
等的圆心角所对两条弦的弦
心距相等.
1.下列图形中既是轴对称图形又是中心对称图形的是( )
A.角 B.等边三角形
C.平行四边形 D.圆
D
2.下列各角是圆心角的是( )
A.∠AOB B.∠CBD
C.∠BCO D.∠DAO
A
随堂演练
C
260o
方法一显然比方法二更简便!
思维拓展
如图,在⊙O中,∠COD=2∠AOB,那么CD=2AB成立吗?CD=2AB也成立吗?请说明理由;如不是,那它们之间的关系又是什么?
⌒ ⌒
A
B
C
D
E
O
答:CD=2AB成立,CD=2AB不成立.
取CD的中点E,连接OE.
那么∠AOB=∠COE=∠DOE,
所以AB=CE=DE, CD=2AB,
弦AB=CE=DE,在△CDE中,CE+DE>CD,即CD<2AB.
⌒ ⌒
⌒
⌒
⌒
⌒
⌒
⌒
弦
圆心
弧
第3章圆的基本性质
3.4 第1课时 圆心角
熊宝宝要过生日了!要把蛋糕平均分成四块,你会分吗?
学习目标
1.经历形成圆的概念的过程,经历探索点与圆
的位置关系的过程.
2.理解圆的概念,用符号、字母正确表示弦和
弧,了解点与圆的位置关系.
3.会在简单条件下判断点与圆的位置关系.
结论:圆是中心对称图形
观察:1.将圆绕圆心旋转180°后,得到的图形与原图形重合吗?由此你得到什么结论呢?
.
O
A
B
180°
获取新知
1.对称性
将圆沿直径所在直线对折,你发现了什么?这就说明圆还是什么图形?
把圆绕圆心旋转任意一个角度呢?仍与原来的圆重合吗?
O
α
结论:圆是旋转对称图形,具有旋转不变性
·
2.旋转不变性
顶点在圆心的角叫做圆心角(central angle).
注意:
1.顶点在圆心;
2.端点在圆上
必须同时满足
例如,如图中,∠NON'就是一个圆心角.
3.圆心角的定义
如图,将圆心角∠AOB绕圆心O旋转到∠A1OB1的位置,你能发现哪些等量关系?为什么?
∵ ∠AOB=∠A1OB1
∴AB=A1B1 ,
AB=A1B1 .
⌒
⌒
·
O
A
B
A1
B1
如图,⊙O与⊙O1是等圆,∠AOB =∠A1OB1=60°,
请问上述结论还成立吗?为什么
·
O
A
B
A1
·
O1
B1
·
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.
①∠AOB=∠COD
②AB=CD
⌒ ⌒
③AB=CD
A
B
O
D
C
4.圆心角定理
如果以⊙O的圆心O为端点作360条射线,把以O为顶点的周角360等分,那么根据圆心角定理,这些射线也把圆360等分.
⌒
每相邻两条射线所成的圆心角是1°的角,
我们把1 °圆心角所对的弧叫做1°的弧.
这样,n°的圆心角所对的弧就
是n°的弧(如图).
5.弧的度数
例1 用直尺和圆规把⊙O(如图)四等分.
例题讲解
作法 如图.
1.作⊙O的一条直径AB.
2.过点O作CD⊥AB,交⊙O于点
C和点D.
点A,B,C,D就把⊙O四等分.
结论:互相垂直的直径,将圆四等分.
例2 求证:在同圆或等圆中,相等的圆心角所对两条弦的弦心距相等.已知:如图,在⊙O中,∠AOB=∠COD,OE是弦AB的弦心距,
OF是弦CD的弦心距.
求证:OE=OF.
证明:∵∠AOB=∠COD,
∴AB=CD(圆心角定理).
∴OE⊥AB,
AE=BE= 1/2 AB(根据什么?).
同理,由OF⊥DC,得DF=CF= 1/2 CD.
∴AE=DF.
又∵OA=OD,
∴Rt△AOE≌Rt△DOF,∴OE=OF.
识记:在同圆或等圆中,相
等的圆心角所对两条弦的弦
心距相等.
1.下列图形中既是轴对称图形又是中心对称图形的是( )
A.角 B.等边三角形
C.平行四边形 D.圆
D
2.下列各角是圆心角的是( )
A.∠AOB B.∠CBD
C.∠BCO D.∠DAO
A
随堂演练
C
260o
方法一显然比方法二更简便!
思维拓展
如图,在⊙O中,∠COD=2∠AOB,那么CD=2AB成立吗?CD=2AB也成立吗?请说明理由;如不是,那它们之间的关系又是什么?
⌒ ⌒
A
B
C
D
E
O
答:CD=2AB成立,CD=2AB不成立.
取CD的中点E,连接OE.
那么∠AOB=∠COE=∠DOE,
所以AB=CE=DE, CD=2AB,
弦AB=CE=DE,在△CDE中,CE+DE>CD,即CD<2AB.
⌒ ⌒
⌒
⌒
⌒
⌒
⌒
⌒
弦
圆心
弧
同课章节目录
