浙教版数学九年级上册同步课件:3.3 第1课时 垂径定理(共15张PPT)
文档属性
| 名称 | 浙教版数学九年级上册同步课件:3.3 第1课时 垂径定理(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 546.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-12 22:23:06 | ||
图片预览






文档简介
(共15张PPT)
第3章圆的基本性质
3.3 第1课时 垂径定理
如图,1 400 多年前,我国隋代建造的赵州石拱
桥主桥拱是圆弧形,它的跨度(弧所对的弦长)是 37.02 m,拱高(弧的中点到弦的距离)为 7.23 m,求赵州桥主桥拱的半径(精确到 0.1 m).
学习目标
1.掌握垂径定理.
2.会运用垂径定理解决一些简单的几何问题.
(2)正三角形是轴对称性图形吗?
有几条对称轴?
(1)什么是轴对称图形
如果一个图形沿着一条直线对折,两侧的图形能
完全重合,这个图形就是轴对称图形。
是
3
(3)圆是否为轴对称图形?如果是,它的对称轴是什么?你能找到多少条对称轴?
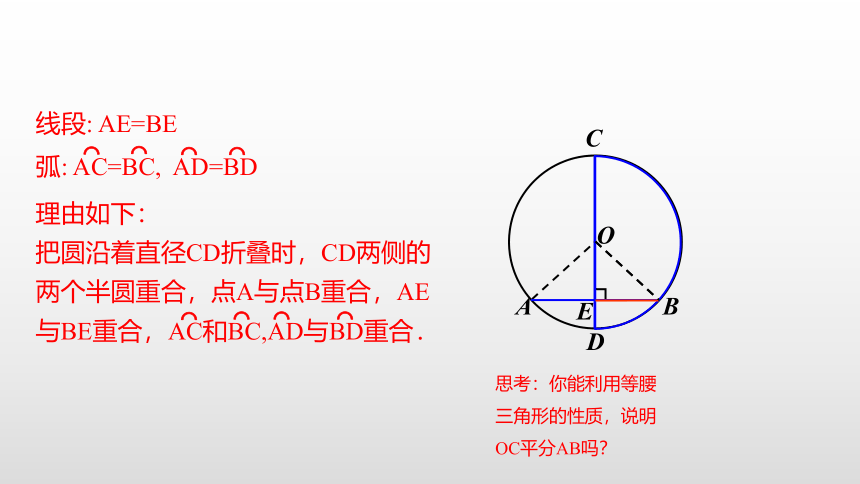
1.在刚才操作的基础上,再作一条和直径CD垂直的弦AB,AB与CD相交于点E,然后沿着直径CD所在的直线把纸折叠,你发现哪些点、线互相重合 如果把能够重合的圆弧叫做相等的圆弧(等弧),有哪些圆弧相等?
·
O
A
B
D
E
C
获取新知
线段: AE=BE
弧: AC=BC, AD=BD
⌒
⌒
⌒
⌒
理由如下:
把圆沿着直径CD折叠时,CD两侧的两个半圆重合,点A与点B重合,AE与BE重合,AC和BC,AD与BD重合.
⌒
⌒
⌒
⌒
·
O
A
B
D
E
C
思考:你能利用等腰
三角形的性质,说明
OC平分AB吗?
垂径定理
垂直于弦的直径平分弦,并且平分弦所对的两条弧.
∵ CD是直径,CD⊥AB,
∴ AE=BE,
⌒
⌒
AC =BC,
⌒
⌒
AD =BD.
推导格式:
·
O
A
B
C
D
E
分一条弧成相等的两条弧的点,叫做这条弧的中点.
例1 已知弧AB,如图,用直尺和圆规求作这条弧的中点.
作法:
⒈ 连结AB.
⒉ 作AB的垂直平分线 CD,交弧AB于点E.
点E就是所求弧AB的中点.
分析:要平分AB,只要画垂直于弦AB的直径.而这条直径应在弦AB的垂直平分线上.因此画AB的垂直平分线就能把AB平分.
⌒
⌒
C
D
A
B
E
例题讲解
例2 一条排水管的截面如图所示。已知排水管的半径OB=10,水面宽AB=16。求截面圆心O到水面的距离。
D
C
10
8
8
圆心到圆的一条弦的距离叫做弦心距.例如,上图中,OC的长就是弦AB的弦心距.
1.下列说法中,正确的是( )
A.直径是圆的对称轴
B.经过圆心的直线是圆的对称轴
C.与圆相交的直线是圆的对称轴
D.与半径垂直的直线是圆的对称轴
B
随堂演练
DE
AD
⌒
⌒
BD
△ODE
16
·
O
A
B
E
4.如图,⊙O的弦AB=8cm ,直径CE⊥AB于D,DC=2cm,求半径OC的长.
解:连接OA,∵ CE⊥AB于D,
∴
设OC=xcm,则OD=x-2,根据勾股定理,得
解得 x=5,
即半径OC的长为5cm.
x2=42+(x-2)2,
·
O
A
B
E
C
D
.
M
C
D
A
B
O
N
思维拓展
D
.
A
B
O
M
A
第3章圆的基本性质
3.3 第1课时 垂径定理
如图,1 400 多年前,我国隋代建造的赵州石拱
桥主桥拱是圆弧形,它的跨度(弧所对的弦长)是 37.02 m,拱高(弧的中点到弦的距离)为 7.23 m,求赵州桥主桥拱的半径(精确到 0.1 m).
学习目标
1.掌握垂径定理.
2.会运用垂径定理解决一些简单的几何问题.
(2)正三角形是轴对称性图形吗?
有几条对称轴?
(1)什么是轴对称图形
如果一个图形沿着一条直线对折,两侧的图形能
完全重合,这个图形就是轴对称图形。
是
3
(3)圆是否为轴对称图形?如果是,它的对称轴是什么?你能找到多少条对称轴?
1.在刚才操作的基础上,再作一条和直径CD垂直的弦AB,AB与CD相交于点E,然后沿着直径CD所在的直线把纸折叠,你发现哪些点、线互相重合 如果把能够重合的圆弧叫做相等的圆弧(等弧),有哪些圆弧相等?
·
O
A
B
D
E
C
获取新知
线段: AE=BE
弧: AC=BC, AD=BD
⌒
⌒
⌒
⌒
理由如下:
把圆沿着直径CD折叠时,CD两侧的两个半圆重合,点A与点B重合,AE与BE重合,AC和BC,AD与BD重合.
⌒
⌒
⌒
⌒
·
O
A
B
D
E
C
思考:你能利用等腰
三角形的性质,说明
OC平分AB吗?
垂径定理
垂直于弦的直径平分弦,并且平分弦所对的两条弧.
∵ CD是直径,CD⊥AB,
∴ AE=BE,
⌒
⌒
AC =BC,
⌒
⌒
AD =BD.
推导格式:
·
O
A
B
C
D
E
分一条弧成相等的两条弧的点,叫做这条弧的中点.
例1 已知弧AB,如图,用直尺和圆规求作这条弧的中点.
作法:
⒈ 连结AB.
⒉ 作AB的垂直平分线 CD,交弧AB于点E.
点E就是所求弧AB的中点.
分析:要平分AB,只要画垂直于弦AB的直径.而这条直径应在弦AB的垂直平分线上.因此画AB的垂直平分线就能把AB平分.
⌒
⌒
C
D
A
B
E
例题讲解
例2 一条排水管的截面如图所示。已知排水管的半径OB=10,水面宽AB=16。求截面圆心O到水面的距离。
D
C
10
8
8
圆心到圆的一条弦的距离叫做弦心距.例如,上图中,OC的长就是弦AB的弦心距.
1.下列说法中,正确的是( )
A.直径是圆的对称轴
B.经过圆心的直线是圆的对称轴
C.与圆相交的直线是圆的对称轴
D.与半径垂直的直线是圆的对称轴
B
随堂演练
DE
AD
⌒
⌒
BD
△ODE
16
·
O
A
B
E
4.如图,⊙O的弦AB=8cm ,直径CE⊥AB于D,DC=2cm,求半径OC的长.
解:连接OA,∵ CE⊥AB于D,
∴
设OC=xcm,则OD=x-2,根据勾股定理,得
解得 x=5,
即半径OC的长为5cm.
x2=42+(x-2)2,
·
O
A
B
E
C
D
.
M
C
D
A
B
O
N
思维拓展
D
.
A
B
O
M
A
同课章节目录
