浙教版数学九年级上册同步课件:2.2 第2课时 用列表法或画树状图法求概率(共23张PPT)
文档属性
| 名称 | 浙教版数学九年级上册同步课件:2.2 第2课时 用列表法或画树状图法求概率(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-12 22:25:01 | ||
图片预览







文档简介
(共23张PPT)
第2章 简单事件的概率
2.2 第2课时 用列表法或画树状图法计算概率
三种事件发生的概率及表示:
①必然事件发生的概率为1,记作P(必然事件)=1;
②不可能事件发生的概率为0,记作P(不可能事件)=0;
③若A为随机事件,则0<P(A)<1
在数学中,我们把事件发生的可能性的大小称为事件发生的概率。
关键是求事件所有可能的结果总数n和其中事件A发生的可能的结果总数(m ≤n)
运用公式 求简单事件发生的概率,在确定各种可能结果发生的可能性相同的基础上,关键是求什么?
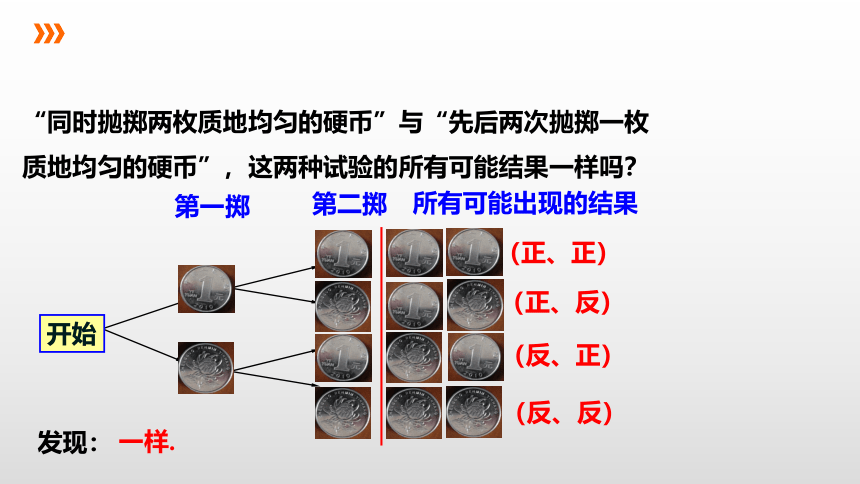
“同时抛掷两枚质地均匀的硬币”与“先后两次抛掷一枚质地均匀的硬币”,这两种试验的所有可能结果一样吗?
开始
第一掷
第二掷
所有可能出现的结果
(正、正)
(正、反)
(反、正)
(反、反)
发现:
一样.
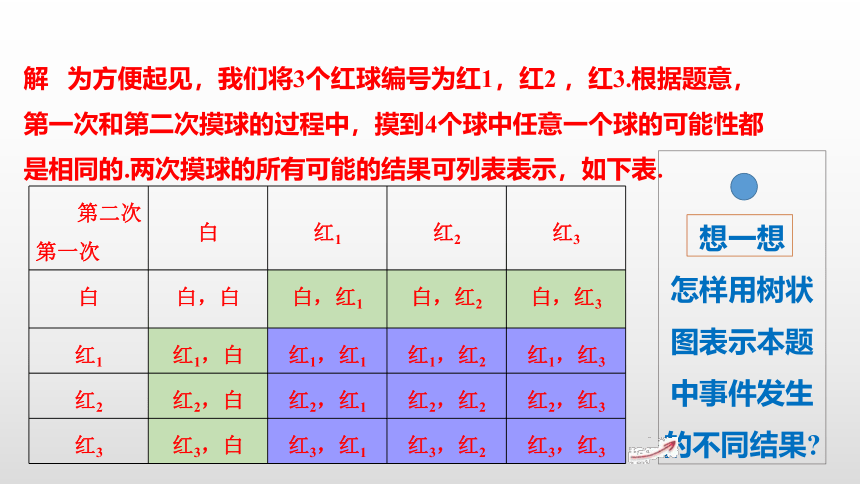
例1 一个布袋里装有4个只有颜色不同的球,其中3个红球,1个白球.从布袋里摸出1个球,记下颜色后放回,搅匀,再摸出1个球.求下列事件发生的概率:
(1)事件A:摸出1个红球,1个白球.
(2)事件B:摸出2个红球.
例题讲解
解 为方便起见,我们将3个红球编号为红1,红2 ,红3.根据题意,第一次和第二次摸球的过程中,摸到4个球中任意一个球的可能性都是相同的.两次摸球的所有可能的结果可列表表示,如下表.
第二次 第一次 白 红1 红2 红3
白 白,白 白,红1 白,红2 白,红3
红1 红1,白 红1,红1 红1,红2 红1,红3
红2 红2,白 红2,红1 红2,红2 红2,红3
红3 红3,白 红3,红1 红3,红2 红3,红3
想一想
怎样用树状图表示本题中事件发生的不同结果
由上表知,n=4×4=16.
(1)事件A包含其中的结果数m=6(如表中绿色部分),
∴
(2)事件B包含其中的结果数m=9(如表中紫色部分),
∴
P(B)= / = 9/16
P(A)= / = 6/16 = 3/8
例2 学校组织春游,安排给九年级三辆车,小明与小慧都可以从这三辆车中任选一辆搭乘.问小明与小慧同车的概率有多大?
解 记这三辆车分别为甲、乙、丙,小明与小慧乘车的所有可能的结果可以列成下表,各种结果发生的可能性相同.
小慧选的车 小明选的车 甲 乙 丙
甲 甲,甲 甲,乙 甲,丙
乙 乙,甲 乙,乙 乙,丙
丙 丙,甲 丙,乙 丙,丙
由上表知,
n=9 ,小明与小慧同车包含其中的结果数m=3 ,
∴
答:小明和小慧同车的概率是 .
例3 如图,转盘的白色扇形和红色扇形的圆心角分别为120°和240°.让转盘自由转动2次,求指针一次落在白色区域,另一次落在红色区域的概率.
分析 很明显,由于两个扇形的圆心角不相等,转盘自由转动1次,指针落在白色区域、红色区域的可能性不相同.如果我们把红色的扇形划分成两个圆心角都是120°的扇形,那么转盘自由转动1次,指针落在各个扇形区域的可能性都应当相同,这样就可以用列举法来求出指针一次落在白色区域,另一次落在红色区域的概率.
解 把红色扇形划分成两个圆心角都是120°的扇形(如图1),分别记为红I,红Ⅱ.让转盘自由转动2次,所有可能的结果如图2所示,且各种结果发生的可能性相同.
白
红I
红Ⅱ
白
红I
红Ⅱ
白
红I
红Ⅱ
红I
红Ⅱ
白
图2
所以n=3×3=9,事件“指针一次落在白色区域,另一次落在红色区域”包含其中的结果数m=4.
∴
想一想:什么时候用“列表法”方便,什么时候用“树形图”方便?
当一次试验涉及两个因素时,且可能出现的结果较多时,为不重复不遗漏地列出所有可能的结果,通常用列表法
当一次试验涉及3个因素或3个以上的因素时,列表法就不方便了,为不重复不遗漏地列出所有可能的结果,通常用树形图
1.同时抛掷两枚质地均匀的硬币,填写下列表格:
第一枚 第二枚 正 反
正 正正
反 反反
由表格可知,出现“一正一反”的概率是____
随堂演练
2.某校九年级共有1,2,3,4四个班,现从这四个班中随机抽取两个班进行一场篮球比赛,则恰好抽到1班和2班的概率是___
3.淘淘和丽丽是非常要好的九年级学生,在5月份进行的物理、化学、生物实验技能考试中,考试科目要求三选一,并且采取抽签方式取得,通过画如图所示的树状图,可知他们两人都抽到物理实验的概率是___
4.如果有两组牌,它们的牌面数字分别是1,2,3,那么从每组牌中各摸出一张牌.
(1)摸出两张牌的数字之和为4的概念为多少?
(2)摸出为两张牌的数字相等的概率为多少?
3
2
(2,3)
(3,3)
(3,2)
(3,1)
(2,2)
(2,1)
(1,3)
(1,2)
(1,1)
1
3
2
1
第二张牌
的牌面数字
第一张牌的
牌面数字
解:(1)P(数字之和为4)= .
(2)P(数字相等)= .
5.现有A、B、C三盘包子,已知A盘中有两个酸菜包和一个糖包,B盘中有一个酸菜包和一个糖包和一个韭菜包,C盘中有一个酸菜包和一个糖包以及一个馒头.老师就爱吃酸菜包,如果老师从每个盘中各选一个包子(馒头除外),那请你帮老师算算选的包子全部是酸菜包的概率是多少?
A
B
C
解:根据题意,画出树状图如下
由树状图得,所有可能出现的结果有18个,它们出现的可能性相等.选的包子全部是酸菜包有2个,所以选的包子全部是酸菜包的概率是:
A盘
B盘
C盘
酸
酸
糖
韭
酸
糖
酸
糖
酸
糖
酸
酸
糖
韭
酸
糖
酸
糖
酸
糖
糖
酸
糖
韭
酸
糖
酸
糖
酸
糖
酸
酸
酸
酸
酸
糖
酸
糖
酸
酸
糖
糖
酸
韭
酸
酸
韭
糖
酸
酸
酸
酸
酸
糖
酸
糖
酸
酸
糖
糖
酸
韭
酸
酸
韭
糖
糖
酸
酸
糖
酸
糖
糖
糖
酸
糖
糖
糖
糖
韭
酸
糖
韭
糖
思维拓展
有三张卡片(形状、大小、颜色、质地都相同),正面分别写上整式x2+1,-x2-2,3.将这三张卡片背面向上洗匀,从中任意抽取一张卡片,记卡片上的整式为A,再从剩下的卡片中任意抽取一张,记卡片上的整式为B,于是得到代数式 .
(1)请用画树状图或列表的方法,写出代数式 所有可能的结果;
(2)求代数式 恰好是分式的概率.
解:(1)画树状图如下:
A B x2+1 -x2-2 3
x2+1
-x2-2
3
或列表如下:
(2)代数式 所有可能的结果共有6种,每种结果出现的可能性相等,其中代数式 是分式的结果有4种,
所以P(代数式 是分式)= .
等可能
第2章 简单事件的概率
2.2 第2课时 用列表法或画树状图法计算概率
三种事件发生的概率及表示:
①必然事件发生的概率为1,记作P(必然事件)=1;
②不可能事件发生的概率为0,记作P(不可能事件)=0;
③若A为随机事件,则0<P(A)<1
在数学中,我们把事件发生的可能性的大小称为事件发生的概率。
关键是求事件所有可能的结果总数n和其中事件A发生的可能的结果总数(m ≤n)
运用公式 求简单事件发生的概率,在确定各种可能结果发生的可能性相同的基础上,关键是求什么?
“同时抛掷两枚质地均匀的硬币”与“先后两次抛掷一枚质地均匀的硬币”,这两种试验的所有可能结果一样吗?
开始
第一掷
第二掷
所有可能出现的结果
(正、正)
(正、反)
(反、正)
(反、反)
发现:
一样.
例1 一个布袋里装有4个只有颜色不同的球,其中3个红球,1个白球.从布袋里摸出1个球,记下颜色后放回,搅匀,再摸出1个球.求下列事件发生的概率:
(1)事件A:摸出1个红球,1个白球.
(2)事件B:摸出2个红球.
例题讲解
解 为方便起见,我们将3个红球编号为红1,红2 ,红3.根据题意,第一次和第二次摸球的过程中,摸到4个球中任意一个球的可能性都是相同的.两次摸球的所有可能的结果可列表表示,如下表.
第二次 第一次 白 红1 红2 红3
白 白,白 白,红1 白,红2 白,红3
红1 红1,白 红1,红1 红1,红2 红1,红3
红2 红2,白 红2,红1 红2,红2 红2,红3
红3 红3,白 红3,红1 红3,红2 红3,红3
想一想
怎样用树状图表示本题中事件发生的不同结果
由上表知,n=4×4=16.
(1)事件A包含其中的结果数m=6(如表中绿色部分),
∴
(2)事件B包含其中的结果数m=9(如表中紫色部分),
∴
P(B)= / = 9/16
P(A)= / = 6/16 = 3/8
例2 学校组织春游,安排给九年级三辆车,小明与小慧都可以从这三辆车中任选一辆搭乘.问小明与小慧同车的概率有多大?
解 记这三辆车分别为甲、乙、丙,小明与小慧乘车的所有可能的结果可以列成下表,各种结果发生的可能性相同.
小慧选的车 小明选的车 甲 乙 丙
甲 甲,甲 甲,乙 甲,丙
乙 乙,甲 乙,乙 乙,丙
丙 丙,甲 丙,乙 丙,丙
由上表知,
n=9 ,小明与小慧同车包含其中的结果数m=3 ,
∴
答:小明和小慧同车的概率是 .
例3 如图,转盘的白色扇形和红色扇形的圆心角分别为120°和240°.让转盘自由转动2次,求指针一次落在白色区域,另一次落在红色区域的概率.
分析 很明显,由于两个扇形的圆心角不相等,转盘自由转动1次,指针落在白色区域、红色区域的可能性不相同.如果我们把红色的扇形划分成两个圆心角都是120°的扇形,那么转盘自由转动1次,指针落在各个扇形区域的可能性都应当相同,这样就可以用列举法来求出指针一次落在白色区域,另一次落在红色区域的概率.
解 把红色扇形划分成两个圆心角都是120°的扇形(如图1),分别记为红I,红Ⅱ.让转盘自由转动2次,所有可能的结果如图2所示,且各种结果发生的可能性相同.
白
红I
红Ⅱ
白
红I
红Ⅱ
白
红I
红Ⅱ
红I
红Ⅱ
白
图2
所以n=3×3=9,事件“指针一次落在白色区域,另一次落在红色区域”包含其中的结果数m=4.
∴
想一想:什么时候用“列表法”方便,什么时候用“树形图”方便?
当一次试验涉及两个因素时,且可能出现的结果较多时,为不重复不遗漏地列出所有可能的结果,通常用列表法
当一次试验涉及3个因素或3个以上的因素时,列表法就不方便了,为不重复不遗漏地列出所有可能的结果,通常用树形图
1.同时抛掷两枚质地均匀的硬币,填写下列表格:
第一枚 第二枚 正 反
正 正正
反 反反
由表格可知,出现“一正一反”的概率是____
随堂演练
2.某校九年级共有1,2,3,4四个班,现从这四个班中随机抽取两个班进行一场篮球比赛,则恰好抽到1班和2班的概率是___
3.淘淘和丽丽是非常要好的九年级学生,在5月份进行的物理、化学、生物实验技能考试中,考试科目要求三选一,并且采取抽签方式取得,通过画如图所示的树状图,可知他们两人都抽到物理实验的概率是___
4.如果有两组牌,它们的牌面数字分别是1,2,3,那么从每组牌中各摸出一张牌.
(1)摸出两张牌的数字之和为4的概念为多少?
(2)摸出为两张牌的数字相等的概率为多少?
3
2
(2,3)
(3,3)
(3,2)
(3,1)
(2,2)
(2,1)
(1,3)
(1,2)
(1,1)
1
3
2
1
第二张牌
的牌面数字
第一张牌的
牌面数字
解:(1)P(数字之和为4)= .
(2)P(数字相等)= .
5.现有A、B、C三盘包子,已知A盘中有两个酸菜包和一个糖包,B盘中有一个酸菜包和一个糖包和一个韭菜包,C盘中有一个酸菜包和一个糖包以及一个馒头.老师就爱吃酸菜包,如果老师从每个盘中各选一个包子(馒头除外),那请你帮老师算算选的包子全部是酸菜包的概率是多少?
A
B
C
解:根据题意,画出树状图如下
由树状图得,所有可能出现的结果有18个,它们出现的可能性相等.选的包子全部是酸菜包有2个,所以选的包子全部是酸菜包的概率是:
A盘
B盘
C盘
酸
酸
糖
韭
酸
糖
酸
糖
酸
糖
酸
酸
糖
韭
酸
糖
酸
糖
酸
糖
糖
酸
糖
韭
酸
糖
酸
糖
酸
糖
酸
酸
酸
酸
酸
糖
酸
糖
酸
酸
糖
糖
酸
韭
酸
酸
韭
糖
酸
酸
酸
酸
酸
糖
酸
糖
酸
酸
糖
糖
酸
韭
酸
酸
韭
糖
糖
酸
酸
糖
酸
糖
糖
糖
酸
糖
糖
糖
糖
韭
酸
糖
韭
糖
思维拓展
有三张卡片(形状、大小、颜色、质地都相同),正面分别写上整式x2+1,-x2-2,3.将这三张卡片背面向上洗匀,从中任意抽取一张卡片,记卡片上的整式为A,再从剩下的卡片中任意抽取一张,记卡片上的整式为B,于是得到代数式 .
(1)请用画树状图或列表的方法,写出代数式 所有可能的结果;
(2)求代数式 恰好是分式的概率.
解:(1)画树状图如下:
A B x2+1 -x2-2 3
x2+1
-x2-2
3
或列表如下:
(2)代数式 所有可能的结果共有6种,每种结果出现的可能性相等,其中代数式 是分式的结果有4种,
所以P(代数式 是分式)= .
等可能
同课章节目录
