1.3 二次函数的性质 同步课件(17张ppt)
文档属性
| 名称 | 1.3 二次函数的性质 同步课件(17张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 954.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-13 00:24:03 | ||
图片预览





文档简介
(共17张PPT)
第1章 二次函数
1.3二次函数的性质
运动员投篮后,篮球运动的路线是一条怎样的曲线 怎样计算篮球达到最高点时的高度?
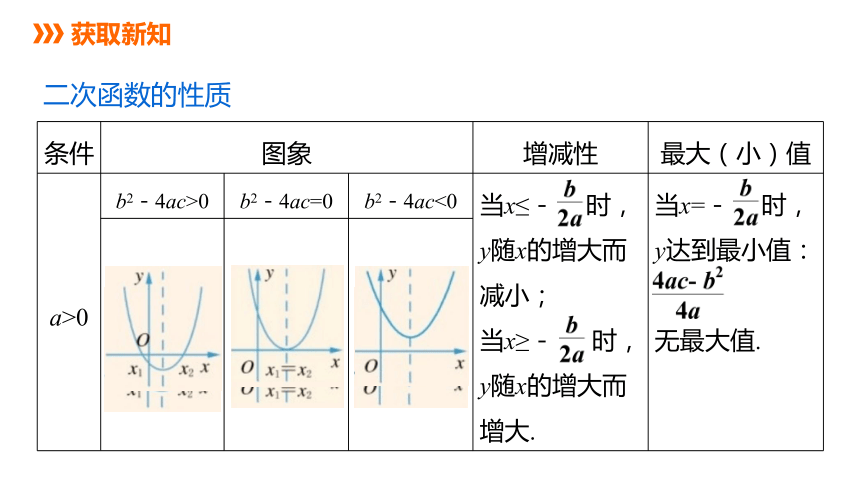
二次函数的性质
条件 图象 增减性 最大(小)值
a>0 b2-4ac>0 b2-4ac=0 b2-4ac<0 当x≤- 时,y随x的增大而减小; 当x≥- 时,y随x的增大而增大. 当x=- 时,
y达到最小值:
无最大值.
获取新知
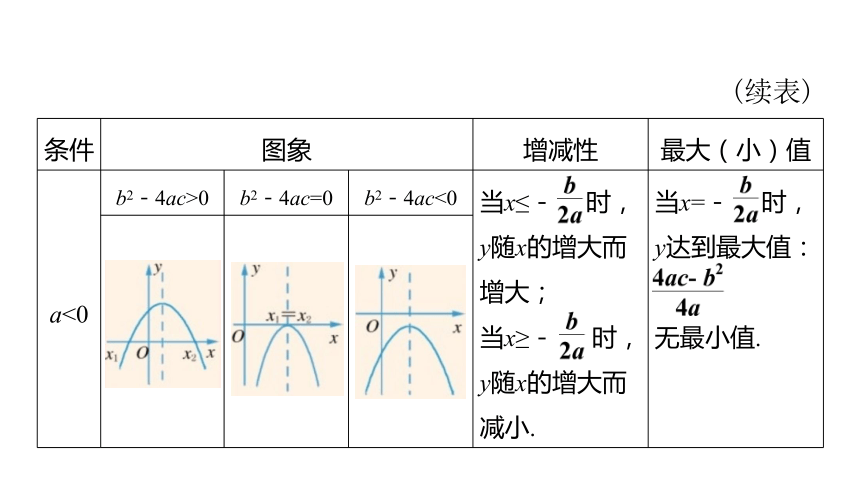
(续表)
条件 图象 增减性 最大(小)值
a<0 b2-4ac>0 b2-4ac=0 b2-4ac<0 当x≤- 时,y随x的增大而增大; 当x≥- 时,y随x的增大而减小. 当x=- 时,
y达到最大值:
无最小值.
例1 已知函数y = -0.5x2-7x+7.5.
(1)求函数图象的顶点坐标、对称轴,以及图象与坐标轴的交点
坐标,并画出函数的大致图象.
(2)自变量x在什么范围内时,y随x 的增大而增大?何时y 随x的增大而减小?并求出函数的最大值或最小值.
(3)根据图象,说出x取哪些值时,① y=0; ② y<0; ③ y>0.
例题讲解
x=-7
20
x
y
10
O
10
-10
30
5
-10
-20
-15
-5
(-7,32)
(0,7.5)
(-15,0)
(1,0)
解:(1)∵a=-0.5,b=-7,c=7.5;
所以函数的顶点坐标是(-7,32),对称轴
是直线x=-7.
由x=0,得y=7.5,即图象与y轴的交点坐标
是(0,7.5);
由y=0,得-0.5x2-7x+7.5=0,解得x1=-15,x2=1,
所以图象与x轴的交点坐标是(-15,0),(1,0).
函数y=-0.5x2-7x+7.5的大致图象如右图:
x=-7
20
x
y
10
O
10
-10
30
5
-10
-20
-15
-5
(-7,32)
(0,7.5)
(-15,0)
(1,0)
(2)由函数y=-0.5x2-7x+7.5的图象可知,
当x≤-7时, y随x的增大而增大;
当x≥-7 时,y随x的增大而减小;
当x=-7时,函数y=-0.5x2-7x+7.5有最大值32.
当-15<x<1时, y>0.
(3)由函数y=-0.5x2-7x+7.5的图象可知, 当x=-15或x=1时,y=0.
当x<-15或x>1时,y<0.
例2 如图所示,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为 .下列结论:①ac<0;②a+b=0;③4ac-b2=4a;
④a+b+c<0.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
C
解析 ①因为抛物线开口向下,与y轴的交点在y轴的正半轴上,所以a<0,c>0,故ac<0;
②由题意知抛物线的对称轴为直线x= ,所以 ,即
a=-b,故a+b=0;
③因为抛物线的顶点纵坐标是1,即 ,所以4ac-b2=4a;
④当x=1时,y=a+b+c.因为抛物线的对称轴为直线x= ,所以当x=1时与当x=0时的函数值相同,观察图象,当x=0时,y>0,所以a+b+c>0.综上所述,①②③正确.
1.二次函数y=x2-8x+1的最小值是( )
A.4 B.-15 C.-4 D.15
2.抛物线y=-3x2-x+4与坐标轴的交点个数是( )
A.3 B.2 C.1 D.0
B
[解析] y=x2-8x+1=(x-4) 2-15,则二次函数y=x2-8x+1的最小值是-15.
[解析] 计算出b2-4ac的值,判断出抛物线y=-3x2-x+4与x轴的交点个数,再结合抛物线y=-3x2-x+4与y轴有1个交点即可得到结论.
A
随堂演练
3.抛物线y=x2-5x-6与x轴的两个交点坐标分别为 .
4.对于二次函数y=-0.5(x-2)2-10,
当x____时,函数值y随x的增大而减小;
当x____时,函数值y随x的增大而增大;
当x=__时,函数取得最___值为____.
(-1,0),(6,0)
≤2
≥2
2
小
-12
5.已知二次函数的图象经过点(-1,-8),顶点坐标为(2,1).
(1)求这个二次函数的表达式;
(2)求这个二次函数的图象与x轴、y轴的交点坐标.
解:(1)设这个二次函数的表达式为y=a(x-2)2+1(a≠0).
把(-1,-8)代入,得-8=9a+1,解得a=-1,
所以这个二次函数的表达式为y=-(x-2)2+1=-x2+4x-3.
(2)令y=0,则-x+4x-3=0,
解得x1=3,x2=1,
所以这个二次函数的图象与x轴的交点坐标是(1,0),(3,0).
令x=0,则y=-3,
所以这个二次函数的图象与y轴的交点坐标是(0,-3).
⑴ 球运动路线的函数解析式和
自变量的取值范围;
⑵ 球在运动中离地面的最大高度。
篮球运动员投篮时,球运动的路线为抛物线的一部分(如图),抛物线的对称轴为x=2.5. 求:
思维拓展
3.05米
4米
2.25米
o
x
y
2.52a+k=2.25
(4-2.5)2a+k=3.05
则:a=-0.2,k=3.5
解: ⑴设函数解析式为:
y=a(x-2.5)2+k,根据题意,得:
∴解析式为:y=-0.2x2+x+2.25,
自变量x的取值范围为:0≤x≤4.
⑵球在运动中离地面的最大高度为3.5米。
3.05米
4米
2.25米
o
x
y
二次函数的性质
条件 图象 增减性 最大(小)值
a>0 b2-4ac>0 b2-4ac=0 b2-4ac<0 当x≤- 时,y随x的增大而减小; 当x≥- 时,y随x的增大而增大. 当x=- 时,
y达到最小值:
无最大值.
(续表)
条件 图象 增减性 最大(小)值
a<0 b2-4ac>0 b2-4ac=0 b2-4ac<0 当x≤- 时,y随x的增大而增大; 当x≥- 时,y随x的增大而减小. 当x=- 时,
y达到最大值:
无最小值.
第1章 二次函数
1.3二次函数的性质
运动员投篮后,篮球运动的路线是一条怎样的曲线 怎样计算篮球达到最高点时的高度?
二次函数的性质
条件 图象 增减性 最大(小)值
a>0 b2-4ac>0 b2-4ac=0 b2-4ac<0 当x≤- 时,y随x的增大而减小; 当x≥- 时,y随x的增大而增大. 当x=- 时,
y达到最小值:
无最大值.
获取新知
(续表)
条件 图象 增减性 最大(小)值
a<0 b2-4ac>0 b2-4ac=0 b2-4ac<0 当x≤- 时,y随x的增大而增大; 当x≥- 时,y随x的增大而减小. 当x=- 时,
y达到最大值:
无最小值.
例1 已知函数y = -0.5x2-7x+7.5.
(1)求函数图象的顶点坐标、对称轴,以及图象与坐标轴的交点
坐标,并画出函数的大致图象.
(2)自变量x在什么范围内时,y随x 的增大而增大?何时y 随x的增大而减小?并求出函数的最大值或最小值.
(3)根据图象,说出x取哪些值时,① y=0; ② y<0; ③ y>0.
例题讲解
x=-7
20
x
y
10
O
10
-10
30
5
-10
-20
-15
-5
(-7,32)
(0,7.5)
(-15,0)
(1,0)
解:(1)∵a=-0.5,b=-7,c=7.5;
所以函数的顶点坐标是(-7,32),对称轴
是直线x=-7.
由x=0,得y=7.5,即图象与y轴的交点坐标
是(0,7.5);
由y=0,得-0.5x2-7x+7.5=0,解得x1=-15,x2=1,
所以图象与x轴的交点坐标是(-15,0),(1,0).
函数y=-0.5x2-7x+7.5的大致图象如右图:
x=-7
20
x
y
10
O
10
-10
30
5
-10
-20
-15
-5
(-7,32)
(0,7.5)
(-15,0)
(1,0)
(2)由函数y=-0.5x2-7x+7.5的图象可知,
当x≤-7时, y随x的增大而增大;
当x≥-7 时,y随x的增大而减小;
当x=-7时,函数y=-0.5x2-7x+7.5有最大值32.
当-15<x<1时, y>0.
(3)由函数y=-0.5x2-7x+7.5的图象可知, 当x=-15或x=1时,y=0.
当x<-15或x>1时,y<0.
例2 如图所示,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为 .下列结论:①ac<0;②a+b=0;③4ac-b2=4a;
④a+b+c<0.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
C
解析 ①因为抛物线开口向下,与y轴的交点在y轴的正半轴上,所以a<0,c>0,故ac<0;
②由题意知抛物线的对称轴为直线x= ,所以 ,即
a=-b,故a+b=0;
③因为抛物线的顶点纵坐标是1,即 ,所以4ac-b2=4a;
④当x=1时,y=a+b+c.因为抛物线的对称轴为直线x= ,所以当x=1时与当x=0时的函数值相同,观察图象,当x=0时,y>0,所以a+b+c>0.综上所述,①②③正确.
1.二次函数y=x2-8x+1的最小值是( )
A.4 B.-15 C.-4 D.15
2.抛物线y=-3x2-x+4与坐标轴的交点个数是( )
A.3 B.2 C.1 D.0
B
[解析] y=x2-8x+1=(x-4) 2-15,则二次函数y=x2-8x+1的最小值是-15.
[解析] 计算出b2-4ac的值,判断出抛物线y=-3x2-x+4与x轴的交点个数,再结合抛物线y=-3x2-x+4与y轴有1个交点即可得到结论.
A
随堂演练
3.抛物线y=x2-5x-6与x轴的两个交点坐标分别为 .
4.对于二次函数y=-0.5(x-2)2-10,
当x____时,函数值y随x的增大而减小;
当x____时,函数值y随x的增大而增大;
当x=__时,函数取得最___值为____.
(-1,0),(6,0)
≤2
≥2
2
小
-12
5.已知二次函数的图象经过点(-1,-8),顶点坐标为(2,1).
(1)求这个二次函数的表达式;
(2)求这个二次函数的图象与x轴、y轴的交点坐标.
解:(1)设这个二次函数的表达式为y=a(x-2)2+1(a≠0).
把(-1,-8)代入,得-8=9a+1,解得a=-1,
所以这个二次函数的表达式为y=-(x-2)2+1=-x2+4x-3.
(2)令y=0,则-x+4x-3=0,
解得x1=3,x2=1,
所以这个二次函数的图象与x轴的交点坐标是(1,0),(3,0).
令x=0,则y=-3,
所以这个二次函数的图象与y轴的交点坐标是(0,-3).
⑴ 球运动路线的函数解析式和
自变量的取值范围;
⑵ 球在运动中离地面的最大高度。
篮球运动员投篮时,球运动的路线为抛物线的一部分(如图),抛物线的对称轴为x=2.5. 求:
思维拓展
3.05米
4米
2.25米
o
x
y
2.52a+k=2.25
(4-2.5)2a+k=3.05
则:a=-0.2,k=3.5
解: ⑴设函数解析式为:
y=a(x-2.5)2+k,根据题意,得:
∴解析式为:y=-0.2x2+x+2.25,
自变量x的取值范围为:0≤x≤4.
⑵球在运动中离地面的最大高度为3.5米。
3.05米
4米
2.25米
o
x
y
二次函数的性质
条件 图象 增减性 最大(小)值
a>0 b2-4ac>0 b2-4ac=0 b2-4ac<0 当x≤- 时,y随x的增大而减小; 当x≥- 时,y随x的增大而增大. 当x=- 时,
y达到最小值:
无最大值.
(续表)
条件 图象 增减性 最大(小)值
a<0 b2-4ac>0 b2-4ac=0 b2-4ac<0 当x≤- 时,y随x的增大而增大; 当x≥- 时,y随x的增大而减小. 当x=- 时,
y达到最大值:
无最小值.
同课章节目录
