5.1.1矩形的性质 课件(共20张PPT)
文档属性
| 名称 | 5.1.1矩形的性质 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-17 08:50:39 | ||
图片预览



文档简介
(共20张PPT)
5.1.1矩形的性质
浙教版 八年级下册
合作学习
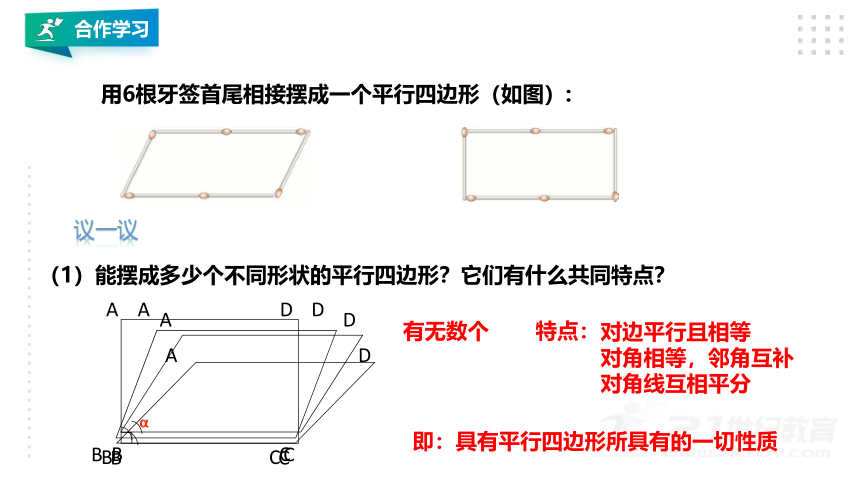
用6根牙签首尾相接摆成一个平行四边形(如图):
(1)能摆成多少个不同形状的平行四边形?它们有什么共同特点?
议一议
α
A D
B C
A D
B C
A D
B C
A D
B C
有无数个
对边平行且相等
对角相等,邻角互补
对角线互相平分
即:具有平行四边形所具有的一切性质
特点:
新知讲解
(3)这个面积最大的平行四边形的内角有什么特点?比较它的两条对角线的长度,你又发现了什么?
(2)在这些平行四边形中,有没有面积最大的一个平行四边形?说出你的理由.
有,当四条边互相垂直时,四边形的面积最大
理由:底不变,互相垂直时高最大,此时面积也最大
内角均为90°
两条对角线长度相等
矩形(长方形)时面积最大
新知讲解
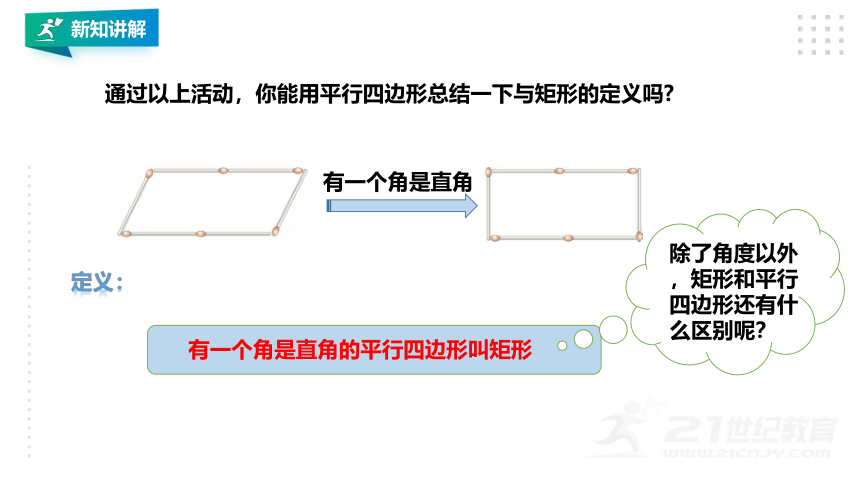
有一个角是直角的平行四边形叫矩形
通过以上活动,你能用平行四边形总结一下与矩形的定义吗
有一个角是直角
定义:
除了角度以外,矩形和平行四边形还有什么区别呢?
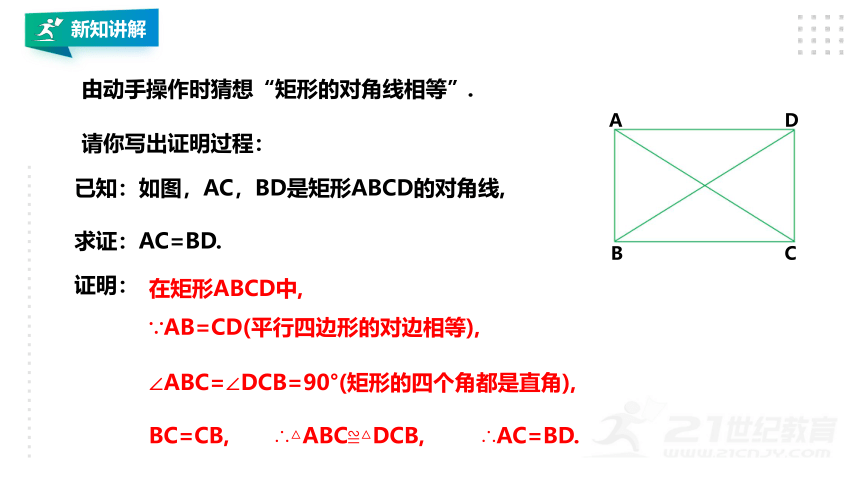
已知:如图,AC,BD是矩形ABCD的对角线,
求证:AC=BD.
由动手操作时猜想“矩形的对角线相等”.
A
B
C
D
证明:
在矩形ABCD中,
∵AB=CD(平行四边形的对边相等),
∠ABC=∠DCB=90°(矩形的四个角都是直角),
BC=CB,
∴△ABC≌△DCB,
∴AC=BD.
新知讲解
请你写出证明过程:
新知讲解
矩形特殊性质:
定理1 矩形的四个角都是直角
定理2 矩形的对角线相等.
总结
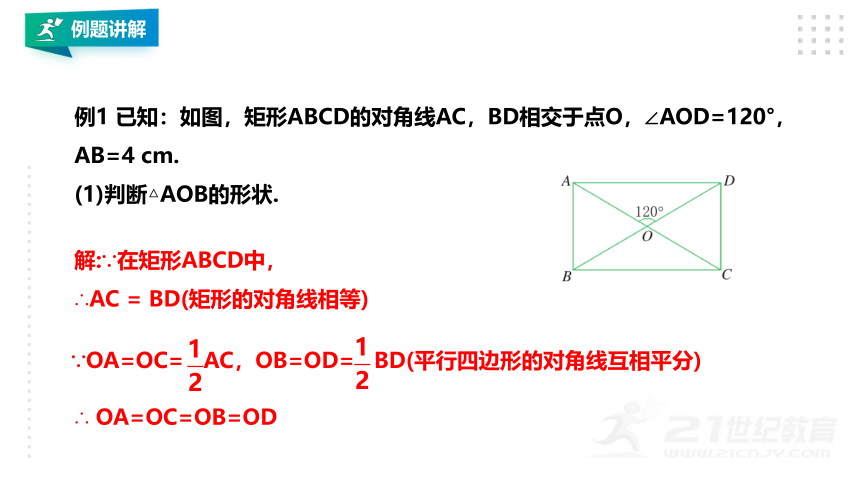
例1 已知:如图,矩形ABCD的对角线AC,BD相交于点O,∠AOD=120°,AB=4 cm.
(1)判断△AOB的形状.
解:∵在矩形ABCD中,
∴AC = BD(矩形的对角线相等)
∵OA=OC= AC,OB=OD= BD(平行四边形的对角线互相平分)
∴ OA=OC=OB=OD
例题讲解
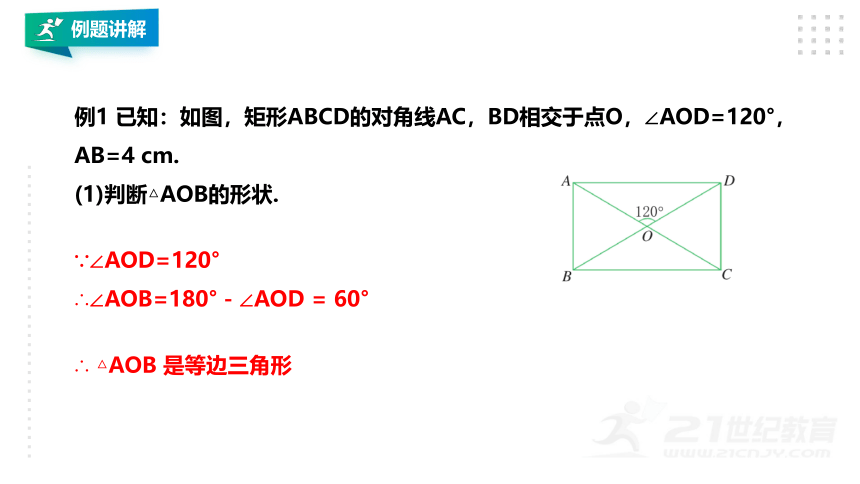
例1 已知:如图,矩形ABCD的对角线AC,BD相交于点O,∠AOD=120°,AB=4 cm.
(1)判断△AOB的形状.
∵∠AOD=120°
∴∠AOB=180°-∠AOD = 60°
∴ △AOB 是等边三角形
例题讲解
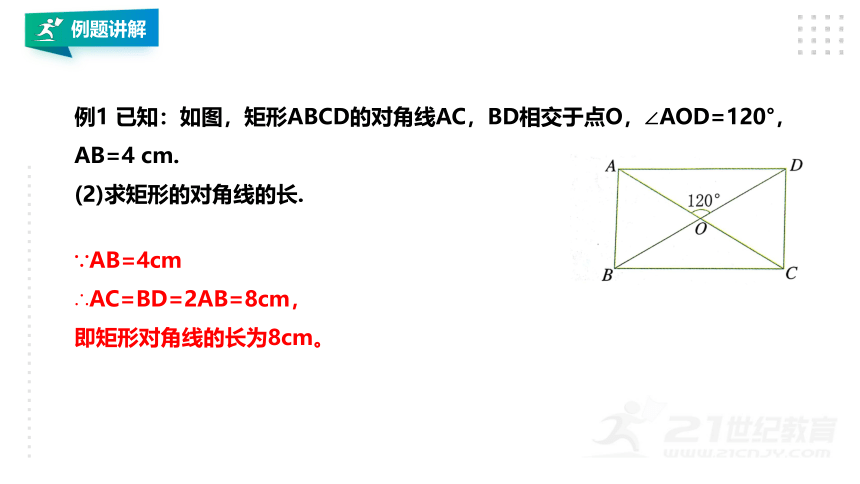
例1 已知:如图,矩形ABCD的对角线AC,BD相交于点O,∠AOD=120°,AB=4 cm.
(2)求矩形的对角线的长.
∵AB=4cm
∴AC=BD=2AB=8cm,
即矩形对角线的长为8cm。
例题讲解
课堂练习
1.如图,矩形ABCD的对角线AC、BD相交于点O,∠ABO=60°,若矩形的对角线长为6.则线段AD的长是( )
A. 3 B. 4
C. 2 D. 3
A
课堂练习
2.如图,在长方形钟面示意图中,时钟的中心在长方形对角线的交点上,长方形宽为 40cm , 钟面数字 2 在长方形的顶点处,则长方形的长为( )cm
A. 80 B. 60 C. 50 D. 40
A
课堂练习
3.一个长方形的三个顶点在平面直角坐标系中的坐标分别为 , , ,那么第四个顶点的坐标为( )
A. B.
C. D.
A
课堂练习
4.如图,已知,矩形ABCD中,AB=3 cm,AD=9 cm,将此矩形折叠,使点B与点D重合,折痕为EF,则AE的长为( )
A. 3cm B. 4cm
C. 5cm D. cm
B
课堂练习
5.如图,在矩形ABCD中,对角线AC与BD交于点O,过点A作AE⊥BD于点E,已知∠EAD=3∠BAE,则∠EOA=________°.
45
课堂练习
如图,折叠长方形的一边AD,使点D落在BC边上的点F处,BC=15,AB=9. 求:
(1)FC的长;
(1)解:∵矩形对边相等,
∴AD=BC=15
∵折叠长方形的一边AD,点D落在BC边上的点F处
∴AF=AD=15,
在Rt△ABF中,由勾股定理得,
∴FC=BC·BF=15-12=3
课堂练习
如图,折叠长方形的一边AD,使点D落在BC边上的点F处,BC=15,AB=9. 求:
(2)EF的长.
(2)解:折叠长方形的一边AD,点D落在BC边上的点F处
∴EF=DE
设DE=x,则EC=9·x,
在Rt△EFC中,由勾股定理得,
即
解得x=5
即EF的长为5.
课堂总结
1.矩形定义:
有一个角是直角的平行四边形叫做矩形.
2.矩形的性质
矩形的四个角都是直角.
矩形的对角线相等.
矩形是中心对称图形,又是轴对称图形
作业布置
课本作业题1-6题
https://www.21cnjy.com/help/help_extract.php
5.1.1矩形的性质
浙教版 八年级下册
合作学习
用6根牙签首尾相接摆成一个平行四边形(如图):
(1)能摆成多少个不同形状的平行四边形?它们有什么共同特点?
议一议
α
A D
B C
A D
B C
A D
B C
A D
B C
有无数个
对边平行且相等
对角相等,邻角互补
对角线互相平分
即:具有平行四边形所具有的一切性质
特点:
新知讲解
(3)这个面积最大的平行四边形的内角有什么特点?比较它的两条对角线的长度,你又发现了什么?
(2)在这些平行四边形中,有没有面积最大的一个平行四边形?说出你的理由.
有,当四条边互相垂直时,四边形的面积最大
理由:底不变,互相垂直时高最大,此时面积也最大
内角均为90°
两条对角线长度相等
矩形(长方形)时面积最大
新知讲解
有一个角是直角的平行四边形叫矩形
通过以上活动,你能用平行四边形总结一下与矩形的定义吗
有一个角是直角
定义:
除了角度以外,矩形和平行四边形还有什么区别呢?
已知:如图,AC,BD是矩形ABCD的对角线,
求证:AC=BD.
由动手操作时猜想“矩形的对角线相等”.
A
B
C
D
证明:
在矩形ABCD中,
∵AB=CD(平行四边形的对边相等),
∠ABC=∠DCB=90°(矩形的四个角都是直角),
BC=CB,
∴△ABC≌△DCB,
∴AC=BD.
新知讲解
请你写出证明过程:
新知讲解
矩形特殊性质:
定理1 矩形的四个角都是直角
定理2 矩形的对角线相等.
总结
例1 已知:如图,矩形ABCD的对角线AC,BD相交于点O,∠AOD=120°,AB=4 cm.
(1)判断△AOB的形状.
解:∵在矩形ABCD中,
∴AC = BD(矩形的对角线相等)
∵OA=OC= AC,OB=OD= BD(平行四边形的对角线互相平分)
∴ OA=OC=OB=OD
例题讲解
例1 已知:如图,矩形ABCD的对角线AC,BD相交于点O,∠AOD=120°,AB=4 cm.
(1)判断△AOB的形状.
∵∠AOD=120°
∴∠AOB=180°-∠AOD = 60°
∴ △AOB 是等边三角形
例题讲解
例1 已知:如图,矩形ABCD的对角线AC,BD相交于点O,∠AOD=120°,AB=4 cm.
(2)求矩形的对角线的长.
∵AB=4cm
∴AC=BD=2AB=8cm,
即矩形对角线的长为8cm。
例题讲解
课堂练习
1.如图,矩形ABCD的对角线AC、BD相交于点O,∠ABO=60°,若矩形的对角线长为6.则线段AD的长是( )
A. 3 B. 4
C. 2 D. 3
A
课堂练习
2.如图,在长方形钟面示意图中,时钟的中心在长方形对角线的交点上,长方形宽为 40cm , 钟面数字 2 在长方形的顶点处,则长方形的长为( )cm
A. 80 B. 60 C. 50 D. 40
A
课堂练习
3.一个长方形的三个顶点在平面直角坐标系中的坐标分别为 , , ,那么第四个顶点的坐标为( )
A. B.
C. D.
A
课堂练习
4.如图,已知,矩形ABCD中,AB=3 cm,AD=9 cm,将此矩形折叠,使点B与点D重合,折痕为EF,则AE的长为( )
A. 3cm B. 4cm
C. 5cm D. cm
B
课堂练习
5.如图,在矩形ABCD中,对角线AC与BD交于点O,过点A作AE⊥BD于点E,已知∠EAD=3∠BAE,则∠EOA=________°.
45
课堂练习
如图,折叠长方形的一边AD,使点D落在BC边上的点F处,BC=15,AB=9. 求:
(1)FC的长;
(1)解:∵矩形对边相等,
∴AD=BC=15
∵折叠长方形的一边AD,点D落在BC边上的点F处
∴AF=AD=15,
在Rt△ABF中,由勾股定理得,
∴FC=BC·BF=15-12=3
课堂练习
如图,折叠长方形的一边AD,使点D落在BC边上的点F处,BC=15,AB=9. 求:
(2)EF的长.
(2)解:折叠长方形的一边AD,点D落在BC边上的点F处
∴EF=DE
设DE=x,则EC=9·x,
在Rt△EFC中,由勾股定理得,
即
解得x=5
即EF的长为5.
课堂总结
1.矩形定义:
有一个角是直角的平行四边形叫做矩形.
2.矩形的性质
矩形的四个角都是直角.
矩形的对角线相等.
矩形是中心对称图形,又是轴对称图形
作业布置
课本作业题1-6题
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
