4.4 平行四边形的判定(1) 课件(共19张PPT)
文档属性
| 名称 | 4.4 平行四边形的判定(1) 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-17 00:00:00 | ||
图片预览



文档简介
(共19张PPT)
4.4 平行四边形的判定(1)
浙教版 八年级下册
新知导入
边
角
对角线
对边平行
对边相等
对角相等
邻角互补
对角线互相平分
平行四边形的性质:
回忆一下
新知讲解
命题“平行四边形的一组对边平行且相等”是真命题吗?你能写出它的逆命题吗?
逆命题:一组对边平行且相等的四边形是平行四边形
你能判断这一命题的真假并证明吗?
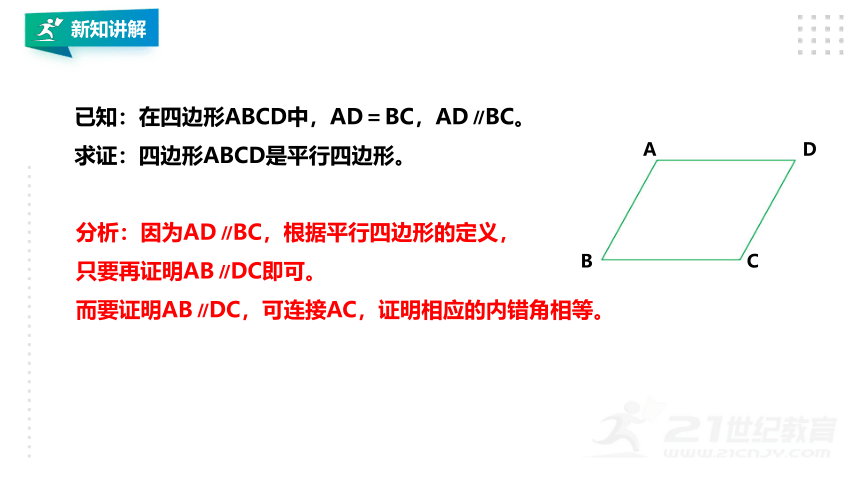
已知:在四边形ABCD中,AD=BC,AD∥BC。
求证:四边形ABCD是平行四边形。
A
D
B
C
分析:因为AD∥BC,根据平行四边形的定义,
只要再证明AB∥DC即可。
而要证明AB∥DC,可连接AC,证明相应的内错角相等。
新知讲解
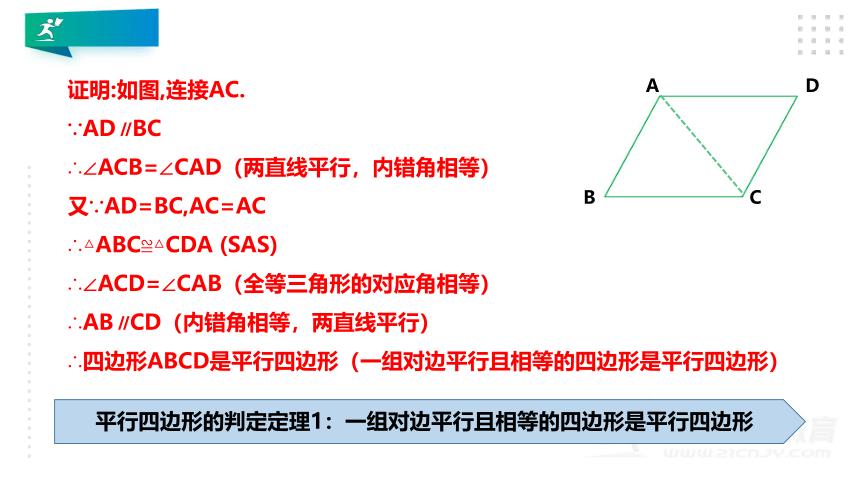
证明:如图,连接AC.
∵AD∥BC
∴∠ACB=∠CAD(两直线平行,内错角相等)
又∵AD=BC,AC=AC
∴△ABC≌△CDA (SAS)
∴∠ACD=∠CAB(全等三角形的对应角相等)
∴AB∥CD(内错角相等,两直线平行)
∴四边形ABCD是平行四边形(一组对边平行且相等的四边形是平行四边形)
A
D
B
C
平行四边形的判定定理1:一组对边平行且相等的四边形是平行四边形
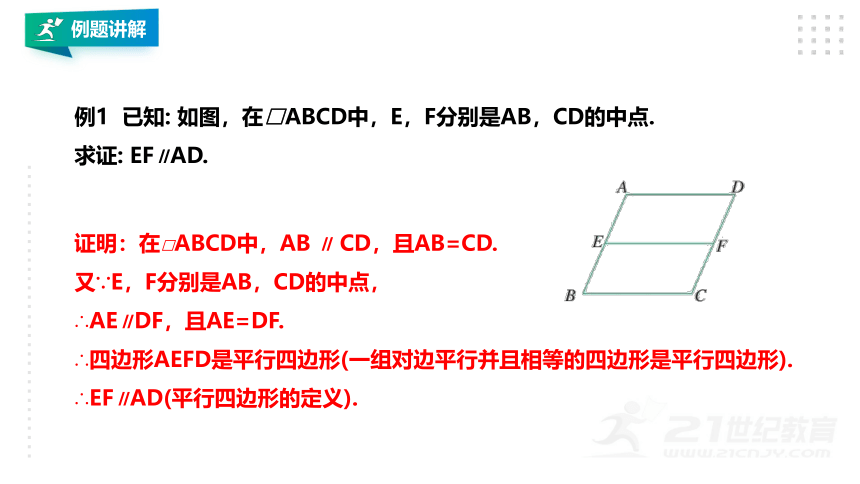
例1 已知: 如图,在□ABCD中,E,F分别是AB,CD的中点.
求证: EF∥AD.
证明:在□ABCD中,AB ∥ CD,且AB=CD.
又∵E,F分别是AB,CD的中点,
∴AE∥DF,且AE=DF.
∴四边形AEFD是平行四边形(一组对边平行并且相等的四边形是平行四边形).
∴EF∥AD(平行四边形的定义).
例题讲解
合作探究
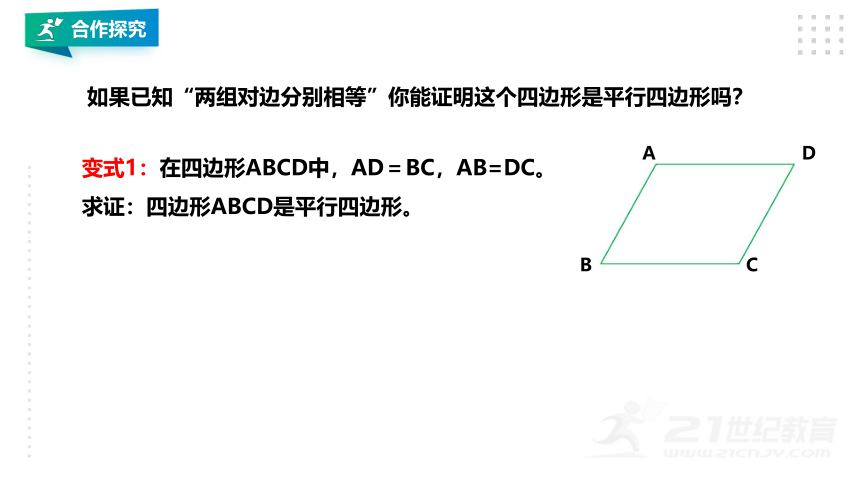
如果已知“两组对边分别相等”你能证明这个四边形是平行四边形吗?
A
D
B
C
变式1:在四边形ABCD中,AD=BC,AB=DC。
求证:四边形ABCD是平行四边形。
证明:如图,连接AC.
∵AD=BC,AB=DC,AC=AC
∴△ABC≌△CDA (SSS)
∴∠ACD=∠CAB(全等三角形的对应角相等)
∴AB∥CD(内错角相等,两直线平行)
∴四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形)
A
D
B
C
平行四边形的判定定理2:两组对边分别相等的四边形是平行四边形
合作探究
课堂练习
1.如图,在 ABCD中,EF∥BC,点H在EF上,GH∥AB,则图中的平行四边形有 ( )
A.3个 B.4个 C.5个 D.6个
C
课堂练习
2.如图,D是直线l外一点,在l上取两点A,B,连结AD,分别以点B,D为圆心,AD,AB的长为半径画弧,两弧交于点C,连结CD,BC,则四边形ABCD是平行四边形,理由是 .
两组对边分别相等的四边形是平行四边形
课堂练习
3.点A,B,C,D在同一平面内,从①AB∥CD,②AB=CD,③BC∥AD,④BC=AD中选两个条件,不能使四边形ABCD是平行四边形的组合是 ( )
A.①② B.②③ C.①③ D.②④
B
课堂练习
[解析] A项,∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,故本选项不符合题意;
B项,②③不能判定四边形ABCD是平行四边形,还可能是等腰梯形,故本选项符合题意;
C项,∵AB∥CD,BC∥AD,
∴四边形ABCD是平行四边形,故本选项不符合题意;
D项,∵AB=CD,BC=AD,
∴四边形ABCD是平行四边形,故本选项不符合题意.
课堂练习
4.如图,在平面直角坐标系中,以O(0,0),A(1,1),B(3,0)为顶点构造平行四边形,下列不能作为该平行四边形第四个顶点坐标的是( )
A.(-3,1) B.(4,1) C.(-2,1) D.(2,-1)
A
课堂练习
5.如图,点E,F分别在 ABCD的边BC,AD上,BE=BC,FD= AD,连结BF,DE.求证:四边形BEDF是平行四边形.
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,且AD=BC.
∵ BE=BC,FD= AD
∴BE=FD,
∴四边形BEDF是平行四边形.
课堂练习
6.如图,E,F是四边形ABCD的对角线AC上的两点,AF=CE,DF=BE,DF∥BE.
求证:四边形ABCD是平行四边形.
证明:∵DF∥BE,
∴∠DFA=∠BEC.
在△ADF和△CBE中,DF=BE,∠DFA=∠BEC,AF=CE
∴△ADF≌△CBE(SAS),
∴AD=BC,∠DAF=∠BCE,
∴AD∥BC,
则四边形ABCD是平行四边形.
课堂总结
从边的角度判定平行四边形
定义:两组对边分别平行的四边形是平行四边形
定理1:一组对边平行且相等的四边形是平行四边形
定理2:两组对边分别相等的四边形是平行四边形
作业布置
课本课后作业第1-5题
https://www.21cnjy.com/help/help_extract.php
4.4 平行四边形的判定(1)
浙教版 八年级下册
新知导入
边
角
对角线
对边平行
对边相等
对角相等
邻角互补
对角线互相平分
平行四边形的性质:
回忆一下
新知讲解
命题“平行四边形的一组对边平行且相等”是真命题吗?你能写出它的逆命题吗?
逆命题:一组对边平行且相等的四边形是平行四边形
你能判断这一命题的真假并证明吗?
已知:在四边形ABCD中,AD=BC,AD∥BC。
求证:四边形ABCD是平行四边形。
A
D
B
C
分析:因为AD∥BC,根据平行四边形的定义,
只要再证明AB∥DC即可。
而要证明AB∥DC,可连接AC,证明相应的内错角相等。
新知讲解
证明:如图,连接AC.
∵AD∥BC
∴∠ACB=∠CAD(两直线平行,内错角相等)
又∵AD=BC,AC=AC
∴△ABC≌△CDA (SAS)
∴∠ACD=∠CAB(全等三角形的对应角相等)
∴AB∥CD(内错角相等,两直线平行)
∴四边形ABCD是平行四边形(一组对边平行且相等的四边形是平行四边形)
A
D
B
C
平行四边形的判定定理1:一组对边平行且相等的四边形是平行四边形
例1 已知: 如图,在□ABCD中,E,F分别是AB,CD的中点.
求证: EF∥AD.
证明:在□ABCD中,AB ∥ CD,且AB=CD.
又∵E,F分别是AB,CD的中点,
∴AE∥DF,且AE=DF.
∴四边形AEFD是平行四边形(一组对边平行并且相等的四边形是平行四边形).
∴EF∥AD(平行四边形的定义).
例题讲解
合作探究
如果已知“两组对边分别相等”你能证明这个四边形是平行四边形吗?
A
D
B
C
变式1:在四边形ABCD中,AD=BC,AB=DC。
求证:四边形ABCD是平行四边形。
证明:如图,连接AC.
∵AD=BC,AB=DC,AC=AC
∴△ABC≌△CDA (SSS)
∴∠ACD=∠CAB(全等三角形的对应角相等)
∴AB∥CD(内错角相等,两直线平行)
∴四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形)
A
D
B
C
平行四边形的判定定理2:两组对边分别相等的四边形是平行四边形
合作探究
课堂练习
1.如图,在 ABCD中,EF∥BC,点H在EF上,GH∥AB,则图中的平行四边形有 ( )
A.3个 B.4个 C.5个 D.6个
C
课堂练习
2.如图,D是直线l外一点,在l上取两点A,B,连结AD,分别以点B,D为圆心,AD,AB的长为半径画弧,两弧交于点C,连结CD,BC,则四边形ABCD是平行四边形,理由是 .
两组对边分别相等的四边形是平行四边形
课堂练习
3.点A,B,C,D在同一平面内,从①AB∥CD,②AB=CD,③BC∥AD,④BC=AD中选两个条件,不能使四边形ABCD是平行四边形的组合是 ( )
A.①② B.②③ C.①③ D.②④
B
课堂练习
[解析] A项,∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,故本选项不符合题意;
B项,②③不能判定四边形ABCD是平行四边形,还可能是等腰梯形,故本选项符合题意;
C项,∵AB∥CD,BC∥AD,
∴四边形ABCD是平行四边形,故本选项不符合题意;
D项,∵AB=CD,BC=AD,
∴四边形ABCD是平行四边形,故本选项不符合题意.
课堂练习
4.如图,在平面直角坐标系中,以O(0,0),A(1,1),B(3,0)为顶点构造平行四边形,下列不能作为该平行四边形第四个顶点坐标的是( )
A.(-3,1) B.(4,1) C.(-2,1) D.(2,-1)
A
课堂练习
5.如图,点E,F分别在 ABCD的边BC,AD上,BE=BC,FD= AD,连结BF,DE.求证:四边形BEDF是平行四边形.
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,且AD=BC.
∵ BE=BC,FD= AD
∴BE=FD,
∴四边形BEDF是平行四边形.
课堂练习
6.如图,E,F是四边形ABCD的对角线AC上的两点,AF=CE,DF=BE,DF∥BE.
求证:四边形ABCD是平行四边形.
证明:∵DF∥BE,
∴∠DFA=∠BEC.
在△ADF和△CBE中,DF=BE,∠DFA=∠BEC,AF=CE
∴△ADF≌△CBE(SAS),
∴AD=BC,∠DAF=∠BCE,
∴AD∥BC,
则四边形ABCD是平行四边形.
课堂总结
从边的角度判定平行四边形
定义:两组对边分别平行的四边形是平行四边形
定理1:一组对边平行且相等的四边形是平行四边形
定理2:两组对边分别相等的四边形是平行四边形
作业布置
课本课后作业第1-5题
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
