4.4 平行四边形的判定(2) 课件(共19张PPT)
文档属性
| 名称 | 4.4 平行四边形的判定(2) 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-17 08:54:27 | ||
图片预览




文档简介
(共19张PPT)
4.4 平行四边形的判定(2)
浙教版 八年级下册
新知导入
定义:两组对边分别平行的四边形是平行四边形
定理1:一组对边平行且相等的四边形是平行四边形
定理2:两组对边分别相等的四边形是平行四边形
我们学过哪些平行四边形的判定定理?
回忆一下
结合平行四边形的性质回忆一下,你还能想到其它方法吗?
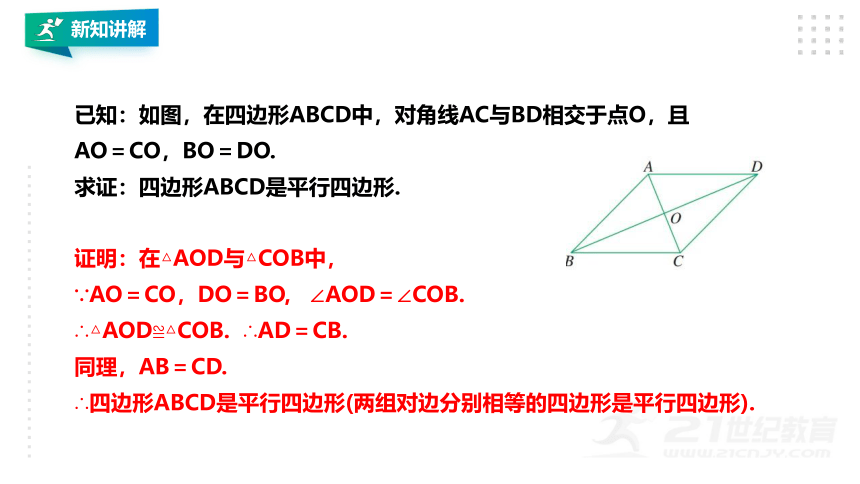
已知:如图,在四边形ABCD中,对角线AC与BD相交于点O,且AO=CO,BO=DO.
求证:四边形ABCD是平行四边形.
证明:在△AOD与△COB中,
∵AO=CO,DO=BO, ∠AOD=∠COB.
∴△AOD≌△COB. ∴AD=CB.
同理,AB=CD.
∴四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形).
新知讲解
新知讲解
从上述证明过程我们可以发现,当已知“对角线互相平分”时,也能证得一个四边形是平行四边形
判定定理4:对角线互相平分的四边形是平行四边形
例2 已知:如图,在□ABCD中,E,F是对角线BD上的两点,且
∠BAE=∠DCF.
求证:四边形AECF是平行四边形.
分析 不难发现,四边形AECF与□ABCD有相同的对角线AC.连结AC,交BD于点O,则AO=CO,BO=DO.因此只要证明BE=DF,就能证明EO=FO.
根据定理“对角线互相平分的四边形是平行四边形”就能证明四边形AECF是平行四边形.
例题讲解
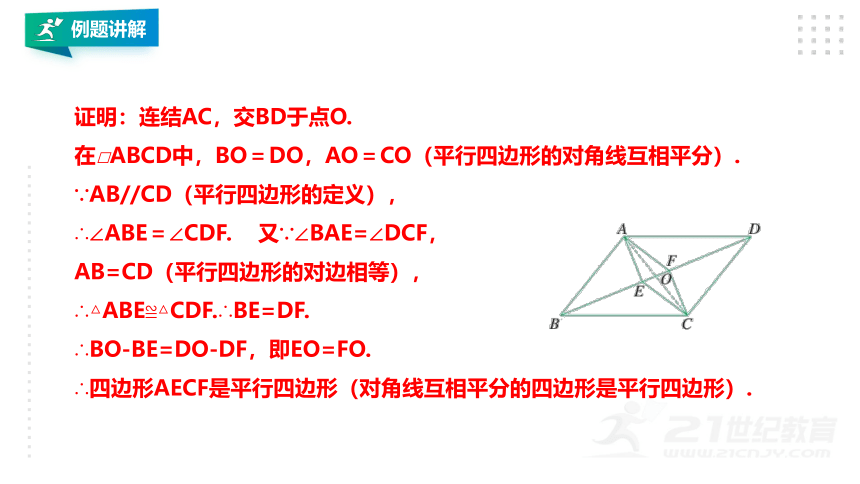
证明:连结AC,交BD于点O.
在□ABCD中,BO=DO,AO=CO(平行四边形的对角线互相平分).
∵AB//CD(平行四边形的定义),
∴∠ABE=∠CDF. 又∵∠BAE=∠DCF,
AB=CD(平行四边形的对边相等),
∴△ABE≌△CDF.∴BE=DF.
∴BO-BE=DO-DF,即EO=FO.
∴四边形AECF是平行四边形(对角线互相平分的四边形是平行四边形).
例题讲解
合作探究
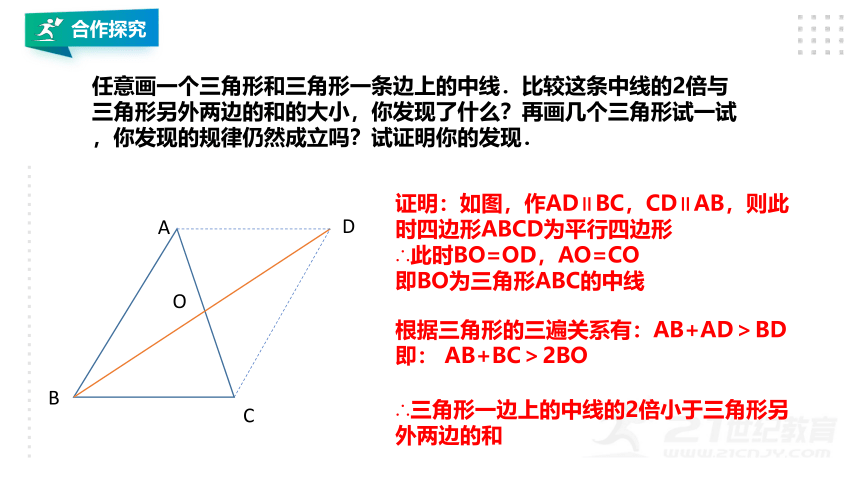
任意画一个三角形和三角形一条边上的中线.比较这条中线的2倍与三角形另外两边的和的大小,你发现了什么?再画几个三角形试一试,你发现的规律仍然成立吗?试证明你的发现.
O
B
C
D
A
根据三角形的三遍关系有:AB+AD>BD
即: AB+BC>2BO
证明:如图,作AD∥BC,CD∥AB,则此时四边形ABCD为平行四边形
∴此时BO=OD,AO=CO
即BO为三角形ABC的中线
∴三角形一边上的中线的2倍小于三角形另外两边的和
课堂练习
1.将两根木条AC,BD的中点重叠,并用钉子固定,则四边形ABCD为平行四边形,理由是 .
对角线互相平分的四边形是平行四边形
课堂练习
2.在四边形ABCD中,对角线AC与BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )
A.AB∥DC,AD∥BC
B.AD∥BC,AB=DC
C.AB∥DC,∠DAB=∠DCB
D.AO=CO,BO=DO
B
课堂练习
[解析] ∵AB∥DC,AD∥BC,
∴四边形ABCD是平行四边形,故选项A不符合题意;
由AD∥BC,AB=DC,无法判定四边形ABCD是平行四边形,故选项B符合题意;
∵AB∥DC,
∴∠ABC+∠DCB=180°.
∵∠DAB=∠DCB,
∴∠ABC+∠DAB=180°,
∴AD∥BC.
又∵AB∥DC,
∴四边形ABCD是平行四边形,故选项C不符合题意;
∵AO=CO,BO=DO,
∴四边形ABCD是平行四边形,故选项D不符合题意.
课堂练习
3.两块含30°角的全等的三角尺能拼出的平行四边形的个数是 ( )
A.1 B.2 C.3 D.无数
[解析] 如图所示,可得到三个不同的平行四边形.
C
课堂练习
4.如图,在 ABCD中,AC⊥AB,AC与BD相交于点O.在同一平面内将△ABC沿AC翻折,得到△AB'C.若四边形ABCD的面积为24 cm2,则翻折后重叠部分(即S△ACE)的面积为 cm2.
6
课堂练习
[解析] ∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,S△ABC=S ABCD=12 cm2.
∵在同一平面内将△ABC沿AC翻折,得到△AB'C,
∴∠B'AC=∠BAC=90°,AB'=AB,S△AB'C=S△ABC=12 cm2,
∴∠BAB'=180°,∴点B,A,B'共线.
连结B'D,
∵AB'∥CD,AB'=AB=CD,
∴四边形ACDB'是平行四边形,
∴B'E=CE,
∴S△ACE= S△AB'C=6 cm2.
课堂练习
5.在平面直角坐标系中,四边形ABCD的四个顶点的坐标分别是A(-4,0),B(0,3),C(4,0),D(0,-3),四边形ABCD是平行四边形吗 请说明理由.
解:四边形ABCD是平行四边形.理由如下:
设O为坐标原点.
由题意,得AC,BD相交于点O,且OA=OC=4,OB=OD=3,
∴四边形ABCD是平行四边形.
课堂练习
6.如图,E,F是 ABCD对角线AC上的两点,AE=CF.求证:四边形BFDE是平行四边形.
证明:连结BD,交AC于点O.
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
又∵AE=CF,
∴OA-AE=OC-CF,即OE=OF,
∴四边形BFDE是平行四边形.
课堂总结
边
对角线
两组对边分别平行的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
两组对边分别相等的四边形是平行四边形
平行四边形的判定
对角线互相平分的四边形是平行四边形
作业布置
课本课后作业第1-5题
https://www.21cnjy.com/help/help_extract.php
4.4 平行四边形的判定(2)
浙教版 八年级下册
新知导入
定义:两组对边分别平行的四边形是平行四边形
定理1:一组对边平行且相等的四边形是平行四边形
定理2:两组对边分别相等的四边形是平行四边形
我们学过哪些平行四边形的判定定理?
回忆一下
结合平行四边形的性质回忆一下,你还能想到其它方法吗?
已知:如图,在四边形ABCD中,对角线AC与BD相交于点O,且AO=CO,BO=DO.
求证:四边形ABCD是平行四边形.
证明:在△AOD与△COB中,
∵AO=CO,DO=BO, ∠AOD=∠COB.
∴△AOD≌△COB. ∴AD=CB.
同理,AB=CD.
∴四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形).
新知讲解
新知讲解
从上述证明过程我们可以发现,当已知“对角线互相平分”时,也能证得一个四边形是平行四边形
判定定理4:对角线互相平分的四边形是平行四边形
例2 已知:如图,在□ABCD中,E,F是对角线BD上的两点,且
∠BAE=∠DCF.
求证:四边形AECF是平行四边形.
分析 不难发现,四边形AECF与□ABCD有相同的对角线AC.连结AC,交BD于点O,则AO=CO,BO=DO.因此只要证明BE=DF,就能证明EO=FO.
根据定理“对角线互相平分的四边形是平行四边形”就能证明四边形AECF是平行四边形.
例题讲解
证明:连结AC,交BD于点O.
在□ABCD中,BO=DO,AO=CO(平行四边形的对角线互相平分).
∵AB//CD(平行四边形的定义),
∴∠ABE=∠CDF. 又∵∠BAE=∠DCF,
AB=CD(平行四边形的对边相等),
∴△ABE≌△CDF.∴BE=DF.
∴BO-BE=DO-DF,即EO=FO.
∴四边形AECF是平行四边形(对角线互相平分的四边形是平行四边形).
例题讲解
合作探究
任意画一个三角形和三角形一条边上的中线.比较这条中线的2倍与三角形另外两边的和的大小,你发现了什么?再画几个三角形试一试,你发现的规律仍然成立吗?试证明你的发现.
O
B
C
D
A
根据三角形的三遍关系有:AB+AD>BD
即: AB+BC>2BO
证明:如图,作AD∥BC,CD∥AB,则此时四边形ABCD为平行四边形
∴此时BO=OD,AO=CO
即BO为三角形ABC的中线
∴三角形一边上的中线的2倍小于三角形另外两边的和
课堂练习
1.将两根木条AC,BD的中点重叠,并用钉子固定,则四边形ABCD为平行四边形,理由是 .
对角线互相平分的四边形是平行四边形
课堂练习
2.在四边形ABCD中,对角线AC与BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )
A.AB∥DC,AD∥BC
B.AD∥BC,AB=DC
C.AB∥DC,∠DAB=∠DCB
D.AO=CO,BO=DO
B
课堂练习
[解析] ∵AB∥DC,AD∥BC,
∴四边形ABCD是平行四边形,故选项A不符合题意;
由AD∥BC,AB=DC,无法判定四边形ABCD是平行四边形,故选项B符合题意;
∵AB∥DC,
∴∠ABC+∠DCB=180°.
∵∠DAB=∠DCB,
∴∠ABC+∠DAB=180°,
∴AD∥BC.
又∵AB∥DC,
∴四边形ABCD是平行四边形,故选项C不符合题意;
∵AO=CO,BO=DO,
∴四边形ABCD是平行四边形,故选项D不符合题意.
课堂练习
3.两块含30°角的全等的三角尺能拼出的平行四边形的个数是 ( )
A.1 B.2 C.3 D.无数
[解析] 如图所示,可得到三个不同的平行四边形.
C
课堂练习
4.如图,在 ABCD中,AC⊥AB,AC与BD相交于点O.在同一平面内将△ABC沿AC翻折,得到△AB'C.若四边形ABCD的面积为24 cm2,则翻折后重叠部分(即S△ACE)的面积为 cm2.
6
课堂练习
[解析] ∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,S△ABC=S ABCD=12 cm2.
∵在同一平面内将△ABC沿AC翻折,得到△AB'C,
∴∠B'AC=∠BAC=90°,AB'=AB,S△AB'C=S△ABC=12 cm2,
∴∠BAB'=180°,∴点B,A,B'共线.
连结B'D,
∵AB'∥CD,AB'=AB=CD,
∴四边形ACDB'是平行四边形,
∴B'E=CE,
∴S△ACE= S△AB'C=6 cm2.
课堂练习
5.在平面直角坐标系中,四边形ABCD的四个顶点的坐标分别是A(-4,0),B(0,3),C(4,0),D(0,-3),四边形ABCD是平行四边形吗 请说明理由.
解:四边形ABCD是平行四边形.理由如下:
设O为坐标原点.
由题意,得AC,BD相交于点O,且OA=OC=4,OB=OD=3,
∴四边形ABCD是平行四边形.
课堂练习
6.如图,E,F是 ABCD对角线AC上的两点,AE=CF.求证:四边形BFDE是平行四边形.
证明:连结BD,交AC于点O.
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
又∵AE=CF,
∴OA-AE=OC-CF,即OE=OF,
∴四边形BFDE是平行四边形.
课堂总结
边
对角线
两组对边分别平行的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
两组对边分别相等的四边形是平行四边形
平行四边形的判定
对角线互相平分的四边形是平行四边形
作业布置
课本课后作业第1-5题
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
