第5章 一元一次不等式复习课件

课件31张PPT。第五章 一元一次不等式复习 不等式不等式的性质1、加减不改变2、乘除正不变4、对称性一元一次
不等式解一元一次不等式解一元一次不等式组在数轴上表示
不等式的解本章结构框图3、乘除负改变5、同向传递性根据下列数量关系列不等式：⑴、a不是正数。⑵、x与y的一半的差大于-3。⑶、y的70%与5的和是非负数。⑷、3与x的倒数的差小于5。⑸、a的立方根不等于a。上述不等式中那些是一元一次不等式 （ ） ⑴、 ⑶ 1、某饮料瓶上有这样的字样：保质期18个月。如果用X（单位：月）表示保质期，那么该饮料的保质期可以用不等式表示为 。2、根据数量关系列不等式：
(1)足球比赛中,每队上场队员人数p不超过11;

(2)y的平方是非负数;

(3)x的3倍与2的和大于4;

(4)y与12的差比它的5倍小;

(5)m与1的相反数的和不小于3.X≤18P≤11y2≥03x+2＞4y-12＜5ym-1≥3写出下列不等式填一填1、用不等号连接：
（1）2 -1;
（2）2+a -1+a;
（3）如x＞0，则 2x -x;
（4）如y＜0, 则 2y -y;
（5） 2（m2+1） -（m2+1）；
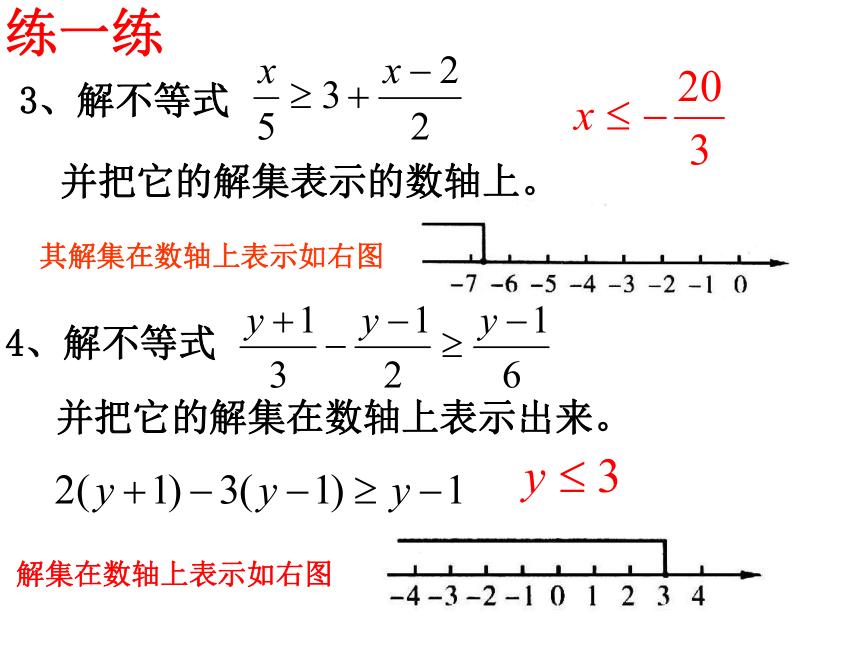
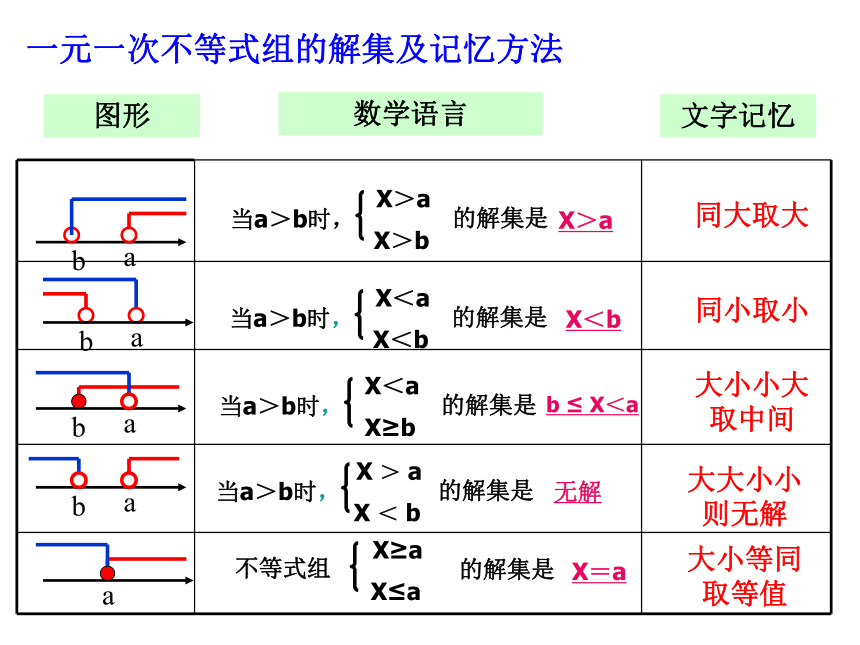
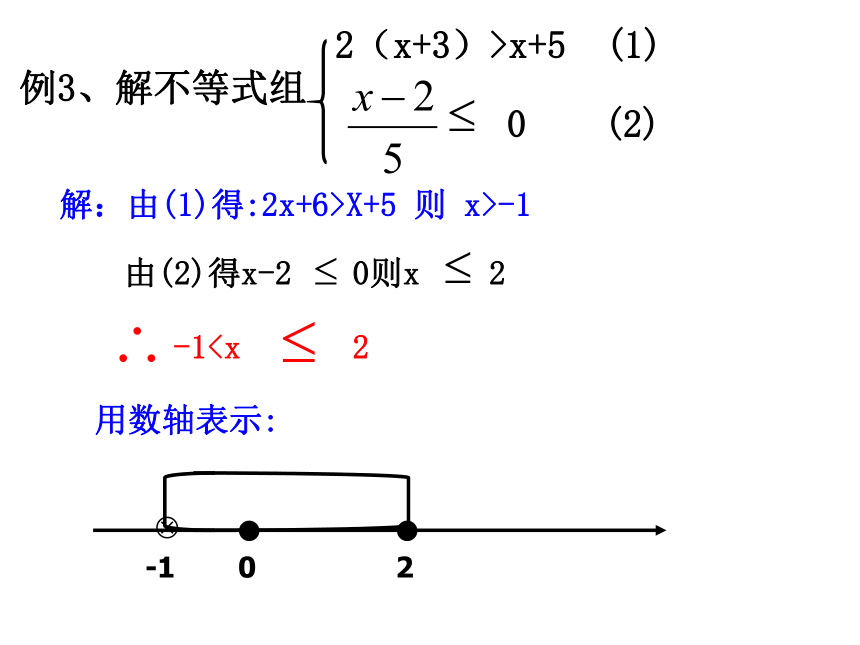
＞＞＞＜＞4、由不等式（m-5）x＞ m-5变形为x＜ 1，则m需满足的条件是 ，3、若a ＞b，且a、b为有理数，则am2 bm2 2、若y= -x+7，且2≤y≤7，则x的取值范围是 ，5、已知不等式3x-m ≤0有4个正整数解，则m的取值范围是 ，0≤x≤5≥m＜512≤m≤15a ≤ 2-2例1、解下列不等式（组）并在数轴上表示出来。在数轴上表示如图所示：（2）不等式 的非负整数解是 。0、1例21、解一元一次不等式,并把解在数轴上表示出来:2、求使不等式3(x-3)-1<2x成立的正整数解。练一练其解集在数轴上表示如右图练一练解集在数轴上表示如右图同大取大X＞a同小取小X＜b大小小大取中间b ≤ X＜a大小等同取等值X＝a大大小小则无解无解文字记忆数学语言图形一元一次不等式组的解集及记忆方法解：由(1)得:2x+6>X+5 则 x>-1用数轴表示:（2）不等式组4≤3x-2≤2x+3的所有整数解的和是 。（3）如果4，3m-2，2m+3这三个数在数轴上所对应的点
从左到右依次排列，则m的取值范围是 。142＜m＜5m≤13例4试一试12、已知不等式3x-m ≤0有0、1两个正整数解，则m的取值范围是 。6≤m＜9 ∴y的正整数解是：1，2，3，4。例5、y取何正整数时，代数式2(y-1)的值不大于10-4（y-3）的值。解：根据题意列出不等式：因为它的解是正数,所以:1、如果关于x的方程3(x+2)=2a+x的根是个负数，且ａ是一个正整数，试确定ｘ的值。练一练 ∴ 根据题意，得 解得 m＞2做一做：填空：
1.若x=3-2a且1/5(x-3)2已知|2x-4|+(3x-y-m)2=0且y<0 则m的范围是( )
3已知不等式4x-a a的正整数解是1, 2，则a的取值范围是( )
4若不等式2x+k<5-x没有正数解则k的范围是( )
5同时满足-3x大于或等于 0与4x+7>0的整数是( )
6不等式(a-1)x1 则a的范围是( )a<1.5m>60 ,-1a<19、如果mA、m-9-n C、1/n >1/m D、m/n >10 ,1C B 1、解关于x的不等式： k(x+3)＞x+4;
解：去括号，得kx+3k＞x+4;
移项得kx-x ＞ 4 -3k ; 得(k-1)x ＞ 4 -3k ;
若k-1=0， 即k=1时，0＞1不成立，
∴不等式无解。
若k-1＞0，即k＞1时，
若k-1＜0，即k＜1时，。 x＞-83、已知不等式3x-a≤0的正整数解是1，2，3，求a的范围变式1:不等式3x-a<0的正整数解为1，2，3，求a的范围变式2:不等式3x-a>0的负整数解为-1，-2，求a的范围变式3:不等式3x-a≥0的负整数解为-1，-2，求a的范围①求此不等式组的整数解
②若上述整数解满足方程ax-3=3a-x，求a的值
例、王海贷款5万元去做生意，贷款月利息10‰ .他决定在半年内利用赚来的钱一次性还清贷款的本息。问王海平均每个月至少要赚多少钱？（精确到100元）月利息=本金×利率本息=本金+利息 例、某网吧有两种收费形式：1、计时制：3元/小时；2、包月制：60元/月,另加1元/小时，请问在什么情况下采用计时制合算,在什么情况下采用包月制合算？ 做一做：1、一次环保知识竞赛共有25道题，规定答对一道题得4分，答错或不答一道题扣1分，在这次竞赛中，小明被评为优秀（85分或85分以上），小明至少答对了几道题？解：设小答对了x道题，则得4x分，另有（25-x）道要扣分，而小明评为优秀，即小明的得分应大于或等于85分，4x-(25-x) ≥85解得： x≥22所以，小明到少答对了22道题，他可能答对22，23，24或25道题。 y1=200×0.75x，即y1=150x，
y2=200×0.8(x-1)，即y2=160x-160,
y1= y2时，150x=160x-160, 解得x=16;
y1 >y2时，150x>160x-160, 解得x<16;
y1< y2时，150x<160x-160, 解得x>16; 2、某单位计划在新年期间组织员工到某地旅游，参如旅游的人数估计为10～25人，甲、乙两家旅行社的服务质量相同，且报价都是每人200元，经过协商，甲旅行社表示可给予每位游客七五折优惠；乙旅行社表示可先免去一位游客的旅游费用，其余游客八折优惠，该单位选择哪一定旅行社支付的旅游费用较少？解：设该单位参加这次旅游的人数是x人，选择甲旅行社时，所需的费用为y1，选择乙旅行社时，所需的费用为y2，则：所以，当人数为16人时，甲、乙两家旅行社的收费相同；当人数为17~25人时，选择甲旅行社费用较少；当人数为10~15人时，选择乙旅行社费用较少。3、某商品的零售价是每件50元，进价是每件35元。经核算，每天商店的各种费用（包括房租、售货员工资等）是120元，还需把商品售出价的10%上缴税款，问商店每天需要出售多少件这样的商品，才能保证商店每天获纯利润在100元以上（不包括100元）？4、某工厂现有甲种原料360kg,乙种原料290kg,计划利用这两种原料生产A,B两种产品共50件,已知生产一件A产品需要甲原料9kg,乙原料3kg,生产一件B产品需要甲原料4kg,乙原料10kg，
（1）设生产X件A种产品，写出X应满足的不等式组。
（2）有哪几种符合的生产方案？
（3）若生产一件A产品可获利700元，生产一件B产品可获利1200元，那么采用哪种生产方案可使生产A、B两种产品的总获利最大？最大利润是多少？