浙教版九年级数学下册《1.3 解直角三角形》教学设计(表格式)
文档属性
| 名称 | 浙教版九年级数学下册《1.3 解直角三角形》教学设计(表格式) |

|
|
| 格式 | doc | ||
| 文件大小 | 445.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-27 21:28:03 | ||
图片预览

文档简介
《1.3.2 解直角三角形》教案
一、教材分析
本节是九年级下册第一章《解直角三角形》第三节的第二课时,是在学生学习了锐角三角函数及解直角三角形后的进一步学习。
本节内容以实际生活中的问题为背景,巩固解直角三角形的初步应用,体验通过添辅助线,将许多有关图形化归为直角三角形问题来解决,渗透用数学知识解决实际问题的数学建模思想。
二、学情分析
学生在学习了解直角三角形后需进一步巩固。但对于通过添加辅助线将多边形转化为三角形的转化过程是缺乏经验积累的,需及时巩固。同时,学生对于用数学知识解决实际问题的基本活动经验为缺乏。
三、教学目标
1、进一步巩固解直角三角形;
2、会用常见添辅助线方法构造直角三角形解决问题;
3、体验用数学知识解决实际问题;
4、渗透、培养学生将计算器用于解决实际问题的能力。
四、教学重、难点
重点:会用常见添辅助线方法构造直角三角形解决问题;
难点:1、添辅助线的方法,将多边形转化为直角三角形是本节课的难点;
2、从实际问题中抽象、提炼出数学问题。
五、教学过程
教学环节 教学内容 设计意图
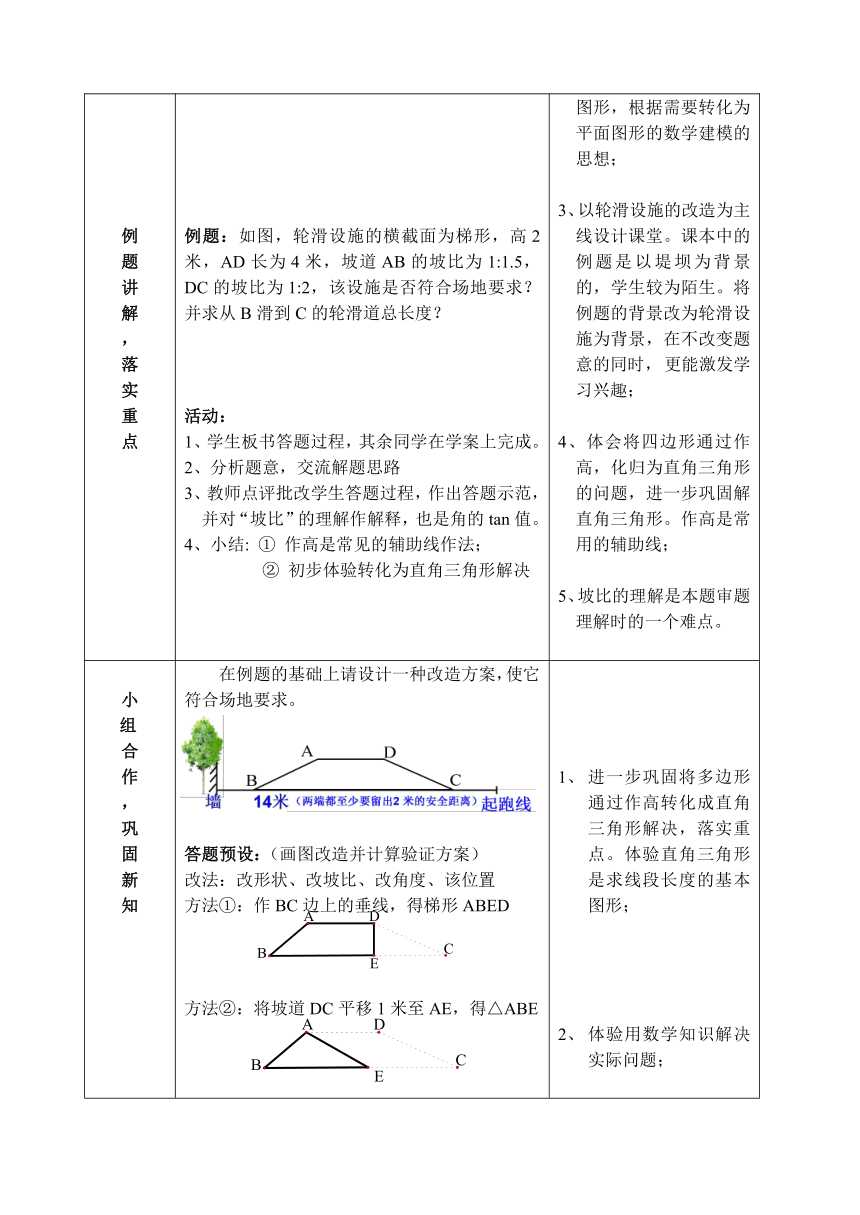
创设情境,提出问题例题讲解,落实重点 结合我校轮滑特色,以学校需要增加轮滑设施为背景引入:在学校操场的一块长为14米的空地上设置一轮滑设施(如图1),为保证安全,两边需留出至少2米的安全距离。设问:如何判断该设施是否符合场地要求?例题:如图,轮滑设施的横截面为梯形,高2米,AD长为4米,坡道AB的坡比为1:1.5,DC的坡比为1:2,该设施是否符合场地要求?并求从B滑到C的轮滑道总长度?活动:1、学生板书答题过程,其余同学在学案上完成。2、分析题意,交流解题思路3、教师点评批改学生答题过程,作出答题示范,并对“坡比”的理解作解释,也是角的tan值。4、小结: ① 作高是常见的辅助线作法;② 初步体验转化为直角三角形解决 1、本节课的设计以轮滑设施为主线,以学生熟悉的情景引入,激发学生学习的兴趣,提出问题,感受学习新知的必要性;2、体验从实际问题中抽象、提炼出几何图形,并从实际问题中的立体图形,根据需要转化为平面图形的数学建模的思想;3、以轮滑设施的改造为主线设计课堂。课本中的例题是以堤坝为背景的,学生较为陌生。将例题的背景改为轮滑设施为背景,在不改变题意的同时, 更能激发学习兴趣;4、体会将四边形通过作高,化归为直角三角形的问题,进一步巩固解直角三角形。作高是常用的辅助线;5、坡比的理解是本题审题理解时的一个难点。
小 组合作,巩固新知 在例题的基础上请设计一种改造方案,使它符合场地要求。答题预设:(画图改造并计算验证方案)改法:改形状、改坡比、改角度、该位置方法①:作BC边上的垂线,得梯形ABED方法②:将坡道DC平移1米至AE,得△ABE方法③:点B向点C方向平移1米(或将倾斜∠AEB=60°)方法④:点D向A平移1米,使∠FEB=60°活动:小组合作交流设计方案并通过计算验证是否符合场地要求2、评价活动方案仿照图3进一步改造轮滑设施,如下:变式:如图4,为增加轮滑的趣味性,AD=3米想在水平滑道上改造一个圆弧形滑道,设计圆弧的半径为3米,与AD’交于M、N两点,弧MN的长为 米,该设计方案能否实现?答案预设:、法一:连结OM、ON,作MN边上的垂线,求出MN的长度与AD比较;法二:连结OA、OD,可得∠AOD=60°,可求出弧AD的长度,与弧MN比较; 进一步巩固将多边形通过作高转化成直角三角形解决,落实重点。体验直角三角形是求线段长度的基本图形;体验用数学知识解决实际问题;3、改造方案是多元化的,可以开拓学生的思维和培养创新能力。此题是课本例题的改编题,源自课本例4。原本的背景是操场跑道的圆弧,现在改造方案的基础上进一步变式,起到承上启下和一题多用的效果;将等腰三角形形通过作垂线转化为直角三角形的问题。作等腰三角形底边上的高是常用的辅助线作法。突破难点;3、渗透、培养学生用计算器解决实际问题的能力;4、变式问题的解答可一题多解,拓展学生的思维。
课堂小结 解题策略:将多边形通过作垂线转化为直角三角形解决(划归思想)把实际生活中的问题抽象成数学问题,并用数学知识加以解决(数学建模思想) 及时小结、梳理
探究活动,提升能力 【有趣的硬币】要求出正九边形的面积,你至少还要添加什么数据? (添加的数据用字母表示)答案预设:添加:半径、边长(直径)辅助线:作底边上的高(如图5)、腰上的高变式:正n边的面积如何表示? 体验从实际生活中提炼出几何图形;一题多解,进一步巩固将多边形问题转化为直角三角形解决;将所求的与已知的集中到同一个直角三角形中;4、体验正n边形都可划归为直角三角形的解题策略。
当堂过关 课本P23,作业题:3、5、6 检测并巩固本节内容
作业布置 完成《作业本》1.3.2节(选做)课本P22, 探究活动
六、板书设计
(图1)
(图2)
(图3)
(图4)
(图5)
(图6)
合作交流
展示区域
1.3.2 解直角三角形
例题板书区域
投影
区域
一、教材分析
本节是九年级下册第一章《解直角三角形》第三节的第二课时,是在学生学习了锐角三角函数及解直角三角形后的进一步学习。
本节内容以实际生活中的问题为背景,巩固解直角三角形的初步应用,体验通过添辅助线,将许多有关图形化归为直角三角形问题来解决,渗透用数学知识解决实际问题的数学建模思想。
二、学情分析
学生在学习了解直角三角形后需进一步巩固。但对于通过添加辅助线将多边形转化为三角形的转化过程是缺乏经验积累的,需及时巩固。同时,学生对于用数学知识解决实际问题的基本活动经验为缺乏。
三、教学目标
1、进一步巩固解直角三角形;
2、会用常见添辅助线方法构造直角三角形解决问题;
3、体验用数学知识解决实际问题;
4、渗透、培养学生将计算器用于解决实际问题的能力。
四、教学重、难点
重点:会用常见添辅助线方法构造直角三角形解决问题;
难点:1、添辅助线的方法,将多边形转化为直角三角形是本节课的难点;
2、从实际问题中抽象、提炼出数学问题。
五、教学过程
教学环节 教学内容 设计意图
创设情境,提出问题例题讲解,落实重点 结合我校轮滑特色,以学校需要增加轮滑设施为背景引入:在学校操场的一块长为14米的空地上设置一轮滑设施(如图1),为保证安全,两边需留出至少2米的安全距离。设问:如何判断该设施是否符合场地要求?例题:如图,轮滑设施的横截面为梯形,高2米,AD长为4米,坡道AB的坡比为1:1.5,DC的坡比为1:2,该设施是否符合场地要求?并求从B滑到C的轮滑道总长度?活动:1、学生板书答题过程,其余同学在学案上完成。2、分析题意,交流解题思路3、教师点评批改学生答题过程,作出答题示范,并对“坡比”的理解作解释,也是角的tan值。4、小结: ① 作高是常见的辅助线作法;② 初步体验转化为直角三角形解决 1、本节课的设计以轮滑设施为主线,以学生熟悉的情景引入,激发学生学习的兴趣,提出问题,感受学习新知的必要性;2、体验从实际问题中抽象、提炼出几何图形,并从实际问题中的立体图形,根据需要转化为平面图形的数学建模的思想;3、以轮滑设施的改造为主线设计课堂。课本中的例题是以堤坝为背景的,学生较为陌生。将例题的背景改为轮滑设施为背景,在不改变题意的同时, 更能激发学习兴趣;4、体会将四边形通过作高,化归为直角三角形的问题,进一步巩固解直角三角形。作高是常用的辅助线;5、坡比的理解是本题审题理解时的一个难点。
小 组合作,巩固新知 在例题的基础上请设计一种改造方案,使它符合场地要求。答题预设:(画图改造并计算验证方案)改法:改形状、改坡比、改角度、该位置方法①:作BC边上的垂线,得梯形ABED方法②:将坡道DC平移1米至AE,得△ABE方法③:点B向点C方向平移1米(或将倾斜∠AEB=60°)方法④:点D向A平移1米,使∠FEB=60°活动:小组合作交流设计方案并通过计算验证是否符合场地要求2、评价活动方案仿照图3进一步改造轮滑设施,如下:变式:如图4,为增加轮滑的趣味性,AD=3米想在水平滑道上改造一个圆弧形滑道,设计圆弧的半径为3米,与AD’交于M、N两点,弧MN的长为 米,该设计方案能否实现?答案预设:、法一:连结OM、ON,作MN边上的垂线,求出MN的长度与AD比较;法二:连结OA、OD,可得∠AOD=60°,可求出弧AD的长度,与弧MN比较; 进一步巩固将多边形通过作高转化成直角三角形解决,落实重点。体验直角三角形是求线段长度的基本图形;体验用数学知识解决实际问题;3、改造方案是多元化的,可以开拓学生的思维和培养创新能力。此题是课本例题的改编题,源自课本例4。原本的背景是操场跑道的圆弧,现在改造方案的基础上进一步变式,起到承上启下和一题多用的效果;将等腰三角形形通过作垂线转化为直角三角形的问题。作等腰三角形底边上的高是常用的辅助线作法。突破难点;3、渗透、培养学生用计算器解决实际问题的能力;4、变式问题的解答可一题多解,拓展学生的思维。
课堂小结 解题策略:将多边形通过作垂线转化为直角三角形解决(划归思想)把实际生活中的问题抽象成数学问题,并用数学知识加以解决(数学建模思想) 及时小结、梳理
探究活动,提升能力 【有趣的硬币】要求出正九边形的面积,你至少还要添加什么数据? (添加的数据用字母表示)答案预设:添加:半径、边长(直径)辅助线:作底边上的高(如图5)、腰上的高变式:正n边的面积如何表示? 体验从实际生活中提炼出几何图形;一题多解,进一步巩固将多边形问题转化为直角三角形解决;将所求的与已知的集中到同一个直角三角形中;4、体验正n边形都可划归为直角三角形的解题策略。
当堂过关 课本P23,作业题:3、5、6 检测并巩固本节内容
作业布置 完成《作业本》1.3.2节(选做)课本P22, 探究活动
六、板书设计
(图1)
(图2)
(图3)
(图4)
(图5)
(图6)
合作交流
展示区域
1.3.2 解直角三角形
例题板书区域
投影
区域
