浙教版八年级数学下册《6.3反比例函数与面积教学设计》教学设计
文档属性
| 名称 | 浙教版八年级数学下册《6.3反比例函数与面积教学设计》教学设计 |
|
|
| 格式 | doc | ||
| 文件大小 | 279.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-27 21:31:49 | ||
图片预览

文档简介
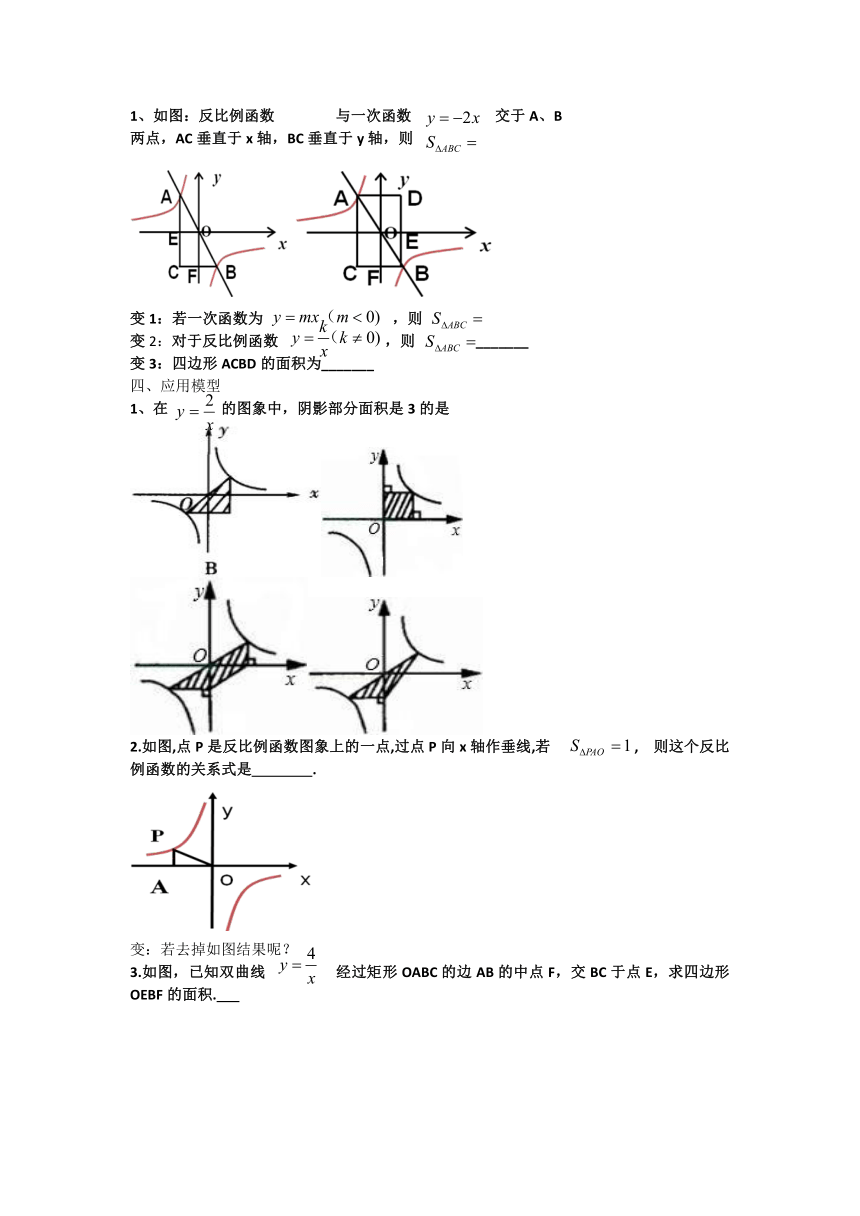
反比例函数与面积教学设计
学习目标:
1、能理解反比例函数图像中具有一定特征的矩形和三角形的面积不变性
2、能熟练运用反比例函数中矩形和三角形的“面积不变性”解决实际问题。
学习重点:能熟练运用反比例函数中矩形和三角形的“面积不变性”解决实际问题。
学习难点:能灵活运用反比例函数中矩形和三角形的“面积不变性”解决实际问题。
教学过程:
一、感受模型
1、如图,点P是反比例函数 图象上的一点,PA⊥x轴于A.则△POA的面积为
2、如图,点P是反比例函数 图象上的一点,PA⊥x轴于A.B点为y轴上的动点,则△PBA的面积为 .
二、发现模型
的三角形、矩形的面积不变性
注意:(1)面积与P的位置无关
(2)当k符号不确定的情况下须分类讨论
三、变式模型
1、如图:反比例函数 与一次函数 交于A、B
两点,AC垂直于x轴,BC垂直于y轴,则
变1:若一次函数为 ,则
变2:对于反比例函数 ,则 _______
变3:四边形ACBD的面积为_______
四、应用模型
1、在 的图象中,阴影部分面积是3的是
2.如图,点P是反比例函数图象上的一点,过点P向x轴作垂线,若 , 则这个反比例函数的关系式是 .
变:若去掉如图结果呢?
3.如图,已知双曲线 经过矩形OABC的边AB的中点F,交BC于点E,求四边形OEBF的面积.
4.反比例函数 与 在第一象限的图象如图所示,作一条平行于x轴的直线分别交双曲线于A、B两点,连接OA、OB,求△AOB的面积.
五、模型之憾
反比例函数 与 的图象如图所示,AC、AB分别垂直于x轴和y轴连接BC,求△ABC的面积.
求面积的方法:
1、直接求
2、间接求
3、利用模型求
六、模型之美
定义:在同一平面坐标系中,反比例函数 的图象称为“美丽四曲线k”.而顶点在“美丽四曲线k”的各个分支上,且两组对边分别与坐标轴平行的矩形称为该“美丽四曲线k”的“伴随矩形”.应用:若点 在“美丽四曲线n”上,求n的值.
探究:试求“美丽四曲线8”的“伴随矩形”的面积.
七、归纳总结
解决反比例函数图像中的面积问题要理解k的几何意义,另外还要明白反比例函数图像中,具有怎样特征的矩形的面积为,具有怎样特征的三角形的面积为。
学习目标:
1、能理解反比例函数图像中具有一定特征的矩形和三角形的面积不变性
2、能熟练运用反比例函数中矩形和三角形的“面积不变性”解决实际问题。
学习重点:能熟练运用反比例函数中矩形和三角形的“面积不变性”解决实际问题。
学习难点:能灵活运用反比例函数中矩形和三角形的“面积不变性”解决实际问题。
教学过程:
一、感受模型
1、如图,点P是反比例函数 图象上的一点,PA⊥x轴于A.则△POA的面积为
2、如图,点P是反比例函数 图象上的一点,PA⊥x轴于A.B点为y轴上的动点,则△PBA的面积为 .
二、发现模型
的三角形、矩形的面积不变性
注意:(1)面积与P的位置无关
(2)当k符号不确定的情况下须分类讨论
三、变式模型
1、如图:反比例函数 与一次函数 交于A、B
两点,AC垂直于x轴,BC垂直于y轴,则
变1:若一次函数为 ,则
变2:对于反比例函数 ,则 _______
变3:四边形ACBD的面积为_______
四、应用模型
1、在 的图象中,阴影部分面积是3的是
2.如图,点P是反比例函数图象上的一点,过点P向x轴作垂线,若 , 则这个反比例函数的关系式是 .
变:若去掉如图结果呢?
3.如图,已知双曲线 经过矩形OABC的边AB的中点F,交BC于点E,求四边形OEBF的面积.
4.反比例函数 与 在第一象限的图象如图所示,作一条平行于x轴的直线分别交双曲线于A、B两点,连接OA、OB,求△AOB的面积.
五、模型之憾
反比例函数 与 的图象如图所示,AC、AB分别垂直于x轴和y轴连接BC,求△ABC的面积.
求面积的方法:
1、直接求
2、间接求
3、利用模型求
六、模型之美
定义:在同一平面坐标系中,反比例函数 的图象称为“美丽四曲线k”.而顶点在“美丽四曲线k”的各个分支上,且两组对边分别与坐标轴平行的矩形称为该“美丽四曲线k”的“伴随矩形”.应用:若点 在“美丽四曲线n”上,求n的值.
探究:试求“美丽四曲线8”的“伴随矩形”的面积.
七、归纳总结
解决反比例函数图像中的面积问题要理解k的几何意义,另外还要明白反比例函数图像中,具有怎样特征的矩形的面积为,具有怎样特征的三角形的面积为。
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
