浙教版八年级数学下册《5.1矩形(2)》教学设计
文档属性
| 名称 | 浙教版八年级数学下册《5.1矩形(2)》教学设计 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-27 21:41:29 | ||
图片预览

文档简介
《5.1矩形(2)》教学设计
教材分析与处理
一、教材的地位和作用
本课是主要研究矩形的判定方法,它不仅是本节的重点,也是以后学习正方形、圆等知识的基础,通过观察试验,归纳证明,培养学生的推理能力和演绎能力,为后面的学习奠定基础。
二、教学目标
1、知识技能
A会证明矩形的两个判定定理。
B会根据矩形的定义和判定定理判定一个四边形是矩形,并能进行有关论证和计算。
2、数学思考
经历探究矩形判定条件的过程,通过探究-猜想-证明-应用,发展学生的合情推理能力,培养主动探究的习惯。
3、解决问题
A探索并掌握矩形的判定方法。
B利用矩形的判定解决问题。
4、情感态度和价值观
A让学生在探索过程中加深对矩形的理解,激发他们的求知欲望。
B进一步体会矩形的结构美和应用美。
三、教学重点和难点
重点:矩形的判定定理。
难点:合理应用矩形的判定定理解决问题,
教学过程:
学习准备
请大家一起来说说矩形的定义是什么?
矩形的定义是____________________.
2.除了用定义判定一个四边形是矩形外,还有其他方法吗 请大家带着这个问题进入探究活动一
二.新知导学
探究活动一
如图,四边形ABCD中,∠D=90°,仅用直角三角板能画出矩形AEFD吗?(要求顶点E、F都在四边形ABCD的边上)
结论:________________________
请你用直角三角板画一个矩形
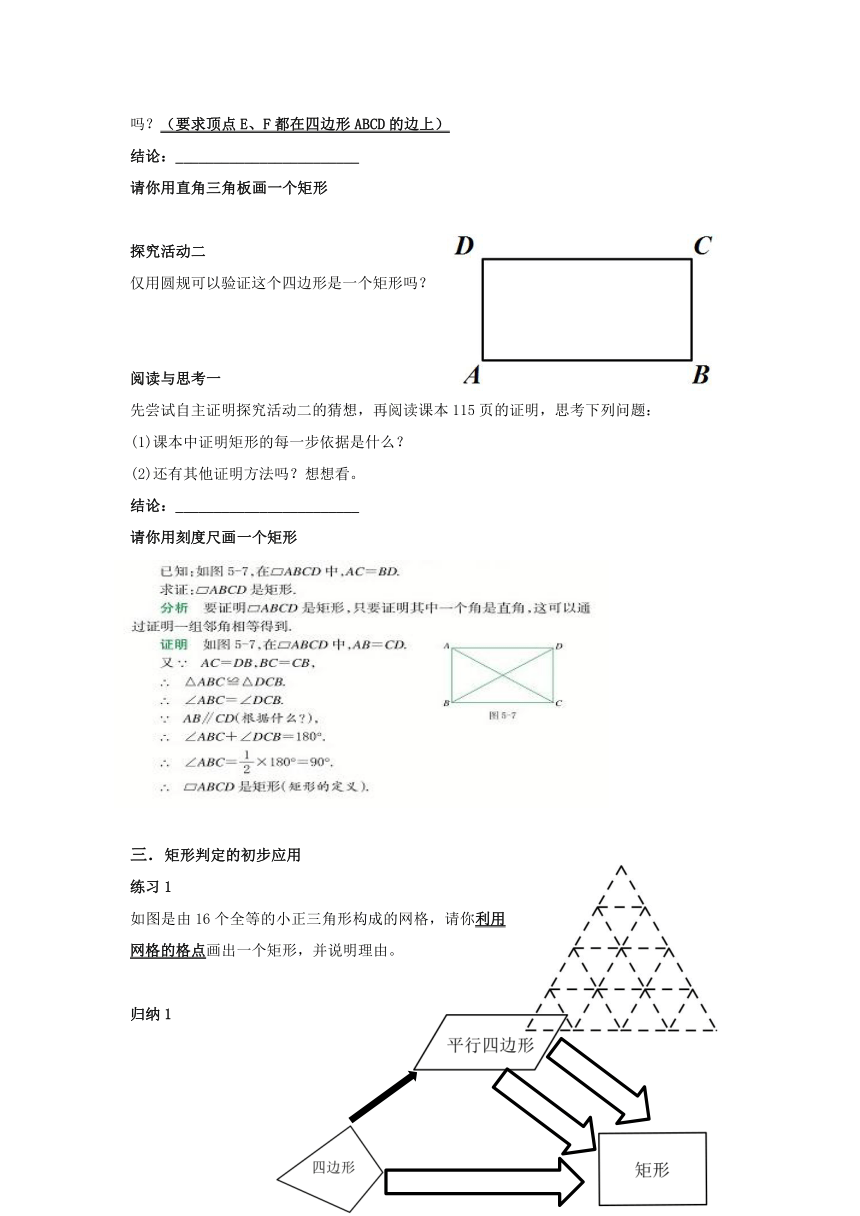
探究活动二
仅用圆规可以验证这个四边形是一个矩形吗?
阅读与思考一
先尝试自主证明探究活动二的猜想,再阅读课本115页的证明,思考下列问题:
(1)课本中证明矩形的每一步依据是什么?
(2)还有其他证明方法吗?想想看。
结论:________________________
请你用刻度尺画一个矩形
三.矩形判定的初步应用
练习1
如图是由16个全等的小正三角形构成的网格,请你利用网格的格点画出一个矩形,并说明理由。
归纳1
练习2
已知:如图,BC是等腰三角形BED的底边ED上的高线,四边形ABEC是平行四边形.
求证:四边形ABCD是矩形
阅读与思考二
先尝试自主做例2,再阅读课本116页例2,思考下列问题:
(1)本题证明矩形的每一步依据是什么?
(2)还有其他证明方法吗
例2 一张四边形纸板ABCD形状如图,它的两条对角线互相垂直.若要从这张纸板中剪出一个矩形,并使它的四个顶点分别落在四边形ABCD的四条边上,可怎样剪?
归纳2
1.取任意四边形的各边中点,连结中点得到的四边形称为中点四边形。
(1)中点四边形的形状是________________.
(2)若原四边形对角线_______________时,中点四边形为矩形。
2.证明一个四边形是矩形一般怎样思考?
梳理
先证明________________,后证明________或_________
直接证明四边形有__________
五.作业布置
必做题:作业本
2.课本P117作业题5
教材分析与处理
一、教材的地位和作用
本课是主要研究矩形的判定方法,它不仅是本节的重点,也是以后学习正方形、圆等知识的基础,通过观察试验,归纳证明,培养学生的推理能力和演绎能力,为后面的学习奠定基础。
二、教学目标
1、知识技能
A会证明矩形的两个判定定理。
B会根据矩形的定义和判定定理判定一个四边形是矩形,并能进行有关论证和计算。
2、数学思考
经历探究矩形判定条件的过程,通过探究-猜想-证明-应用,发展学生的合情推理能力,培养主动探究的习惯。
3、解决问题
A探索并掌握矩形的判定方法。
B利用矩形的判定解决问题。
4、情感态度和价值观
A让学生在探索过程中加深对矩形的理解,激发他们的求知欲望。
B进一步体会矩形的结构美和应用美。
三、教学重点和难点
重点:矩形的判定定理。
难点:合理应用矩形的判定定理解决问题,
教学过程:
学习准备
请大家一起来说说矩形的定义是什么?
矩形的定义是____________________.
2.除了用定义判定一个四边形是矩形外,还有其他方法吗 请大家带着这个问题进入探究活动一
二.新知导学
探究活动一
如图,四边形ABCD中,∠D=90°,仅用直角三角板能画出矩形AEFD吗?(要求顶点E、F都在四边形ABCD的边上)
结论:________________________
请你用直角三角板画一个矩形
探究活动二
仅用圆规可以验证这个四边形是一个矩形吗?
阅读与思考一
先尝试自主证明探究活动二的猜想,再阅读课本115页的证明,思考下列问题:
(1)课本中证明矩形的每一步依据是什么?
(2)还有其他证明方法吗?想想看。
结论:________________________
请你用刻度尺画一个矩形
三.矩形判定的初步应用
练习1
如图是由16个全等的小正三角形构成的网格,请你利用网格的格点画出一个矩形,并说明理由。
归纳1
练习2
已知:如图,BC是等腰三角形BED的底边ED上的高线,四边形ABEC是平行四边形.
求证:四边形ABCD是矩形
阅读与思考二
先尝试自主做例2,再阅读课本116页例2,思考下列问题:
(1)本题证明矩形的每一步依据是什么?
(2)还有其他证明方法吗
例2 一张四边形纸板ABCD形状如图,它的两条对角线互相垂直.若要从这张纸板中剪出一个矩形,并使它的四个顶点分别落在四边形ABCD的四条边上,可怎样剪?
归纳2
1.取任意四边形的各边中点,连结中点得到的四边形称为中点四边形。
(1)中点四边形的形状是________________.
(2)若原四边形对角线_______________时,中点四边形为矩形。
2.证明一个四边形是矩形一般怎样思考?
梳理
先证明________________,后证明________或_________
直接证明四边形有__________
五.作业布置
必做题:作业本
2.课本P117作业题5
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
