浙教版九年级数学下册3.4 简单几何体的表面展开图---直棱柱教学设计
文档属性
| 名称 | 浙教版九年级数学下册3.4 简单几何体的表面展开图---直棱柱教学设计 | 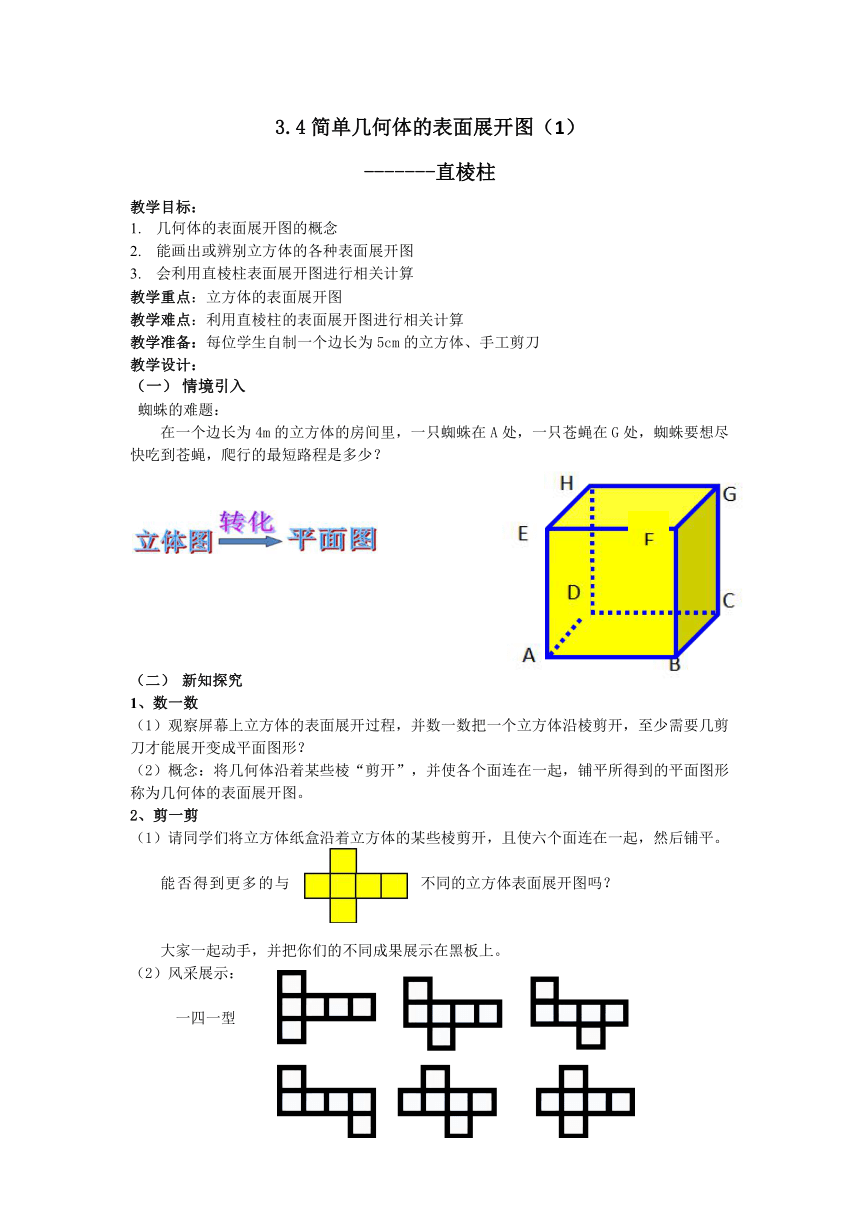 | |
| 格式 | docx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-28 06:38:35 | ||
图片预览


文档简介
3.4简单几何体的表面展开图(1)
-------直棱柱
教学目标:
几何体的表面展开图的概念
能画出或辨别立方体的各种表面展开图
会利用直棱柱表面展开图进行相关计算
教学重点:立方体的表面展开图
教学难点:利用直棱柱的表面展开图进行相关计算
教学准备:每位学生自制一个边长为5cm的立方体、手工剪刀
教学设计:
情境引入
蜘蛛的难题:
在一个边长为4m的立方体的房间里,一只蜘蛛在A处,一只苍蝇在G处,蜘蛛要想尽快吃到苍蝇,爬行的最短路程是多少?
新知探究
数一数
(1)观察屏幕上立方体的表面展开过程,并数一数把一个立方体沿棱剪开,至少需要几剪刀才能展开变成平面图形?
(2)概念:将几何体沿着某些棱“剪开”,并使各个面连在一起,铺平所得到的平面图形称为几何体的表面展开图。
2、剪一剪
(1)请同学们将立方体纸盒沿着立方体的某些棱剪开,且使六个面连在一起,然后铺平。
能否得到更多的与 不同的立方体表面展开图吗?
大家一起动手,并把你们的不同成果展示在黑板上。
(2)风采展示:
一四一型
一三二型
三个二型
二个三型
记忆口诀:“一三二”, “一四一”,“一”在同层可任意;“三个二”成阶梯,“二个三”,“日”字连;异层 “日”字连,整体没有“田”。
3、辨一辨
下面的图形是不是立方体的表面展开图吗?
4、填一填
(1)你能在立方体的表面展开图中找到相对面吗?
(2)如图是一个正方体纸盒的展开图,图中的6个正方形中分别已填入了-1、7、2 、a、b、c,使展开图沿虚线折叠成正方体后相对面上的两个数互为相反数,求:a= ;b= ;c=
(3)请分别用1,2,3,4,5,6中的同一个数字表示立方体和它的展开图中各对对应的面.
归纳:立方体表面展开图的规律
展开剪七刀,对面不相连,构型分四种,日字异层现,整体没有田。
5、算一算
(1)发挥你的想象,下列分别为哪些几何体的表面展开图?
(2)例1:如图为了生产这种包装盒,需要先画出展开图纸样。
如图是五位设计师设计的五种纸样,它们都正确吗?
从已知正确的纸样中选出一种,标上尺寸;
利用你所选的这种纸样,求出包装盒的侧面积和表面积。
归纳:直棱柱的相关计算:
侧面积=底面周长×侧棱长(高)
全面积=侧面积+底面积
(3)现在你能解决蜘蛛的难题了吗?怎么爬?最短路径是多少?
6、议一议(变式拓展)
如果换成下面长方体的房间,又会怎么样呢?
如图,有一长方体形的房间,长6米,宽4米,高5米。一只蜘蛛在A处,一只苍蝇在G处,试问,蜘蛛去捉苍蝇需要爬行的最短路程是多少?
(三)想一想
这节课你有什么收获?
-------直棱柱
教学目标:
几何体的表面展开图的概念
能画出或辨别立方体的各种表面展开图
会利用直棱柱表面展开图进行相关计算
教学重点:立方体的表面展开图
教学难点:利用直棱柱的表面展开图进行相关计算
教学准备:每位学生自制一个边长为5cm的立方体、手工剪刀
教学设计:
情境引入
蜘蛛的难题:
在一个边长为4m的立方体的房间里,一只蜘蛛在A处,一只苍蝇在G处,蜘蛛要想尽快吃到苍蝇,爬行的最短路程是多少?
新知探究
数一数
(1)观察屏幕上立方体的表面展开过程,并数一数把一个立方体沿棱剪开,至少需要几剪刀才能展开变成平面图形?
(2)概念:将几何体沿着某些棱“剪开”,并使各个面连在一起,铺平所得到的平面图形称为几何体的表面展开图。
2、剪一剪
(1)请同学们将立方体纸盒沿着立方体的某些棱剪开,且使六个面连在一起,然后铺平。
能否得到更多的与 不同的立方体表面展开图吗?
大家一起动手,并把你们的不同成果展示在黑板上。
(2)风采展示:
一四一型
一三二型
三个二型
二个三型
记忆口诀:“一三二”, “一四一”,“一”在同层可任意;“三个二”成阶梯,“二个三”,“日”字连;异层 “日”字连,整体没有“田”。
3、辨一辨
下面的图形是不是立方体的表面展开图吗?
4、填一填
(1)你能在立方体的表面展开图中找到相对面吗?
(2)如图是一个正方体纸盒的展开图,图中的6个正方形中分别已填入了-1、7、2 、a、b、c,使展开图沿虚线折叠成正方体后相对面上的两个数互为相反数,求:a= ;b= ;c=
(3)请分别用1,2,3,4,5,6中的同一个数字表示立方体和它的展开图中各对对应的面.
归纳:立方体表面展开图的规律
展开剪七刀,对面不相连,构型分四种,日字异层现,整体没有田。
5、算一算
(1)发挥你的想象,下列分别为哪些几何体的表面展开图?
(2)例1:如图为了生产这种包装盒,需要先画出展开图纸样。
如图是五位设计师设计的五种纸样,它们都正确吗?
从已知正确的纸样中选出一种,标上尺寸;
利用你所选的这种纸样,求出包装盒的侧面积和表面积。
归纳:直棱柱的相关计算:
侧面积=底面周长×侧棱长(高)
全面积=侧面积+底面积
(3)现在你能解决蜘蛛的难题了吗?怎么爬?最短路径是多少?
6、议一议(变式拓展)
如果换成下面长方体的房间,又会怎么样呢?
如图,有一长方体形的房间,长6米,宽4米,高5米。一只蜘蛛在A处,一只苍蝇在G处,试问,蜘蛛去捉苍蝇需要爬行的最短路程是多少?
(三)想一想
这节课你有什么收获?
