1.4.2二次函数的应用 课件(共17张PPT)
文档属性
| 名称 | 1.4.2二次函数的应用 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 940.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-20 14:59:46 | ||
图片预览






文档简介
(共17张PPT)
1.4.2二次函数的应用
浙教版 九年级上册
教学目标
知识目标:继续经历利用二次函数解决实际最值问题的过程.
能力目标:会综合运用二次函数和其他数学知识解决如有关距离等函数最值问题.
重点:利用二次函数的知识对现实问题进行数学地分析,即用数学的方式表示问题以及用数学的方法解决问题。
难点:将现实问题数学化,情景比较复杂。
新知导入
由于抛物线 y = ax 2 + bx + c 的顶点是最低(高)点,
当 时,二次函数 y = ax 2 + bx + c 有最小(大) 值
想一想:如何求出二次函数 y = ax 2 + bx + c 的最小(大)值?
新知讲解
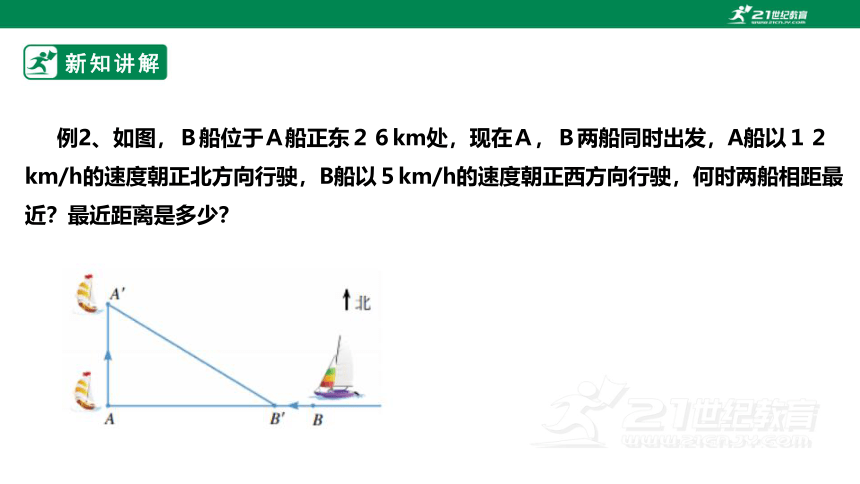
例2、如图,B船位于A船正东26km处,现在A,B两船同时出发,A船以12km/h的速度朝正北方向行驶,B船以5km/h的速度朝正西方向行驶,何时两船相距最近?最近距离是多少?
新知讲解
解:设经过t(h)后,A,B两船分别到达A’,B’处,则
(t>0)
当13t-10=0,即时,有最小值576
所以当时,(km).
答:经过h,两船之间的距离最近,最近距离为24km.
新知讲解
例3、某超市销售一种饮料,每瓶进价为9元.经市场调查表明,当售价在10元到14元之间(含10元,14元)浮动时,每瓶售价每增加0.5元,日均销售量减少40瓶;当售价为每瓶12元时,日均销售量为400瓶.问销售价格定为每瓶多少元时,所得日均毛利润(每瓶毛利润=每瓶售价-每瓶进价)最大?最大日均毛利润为多少元?
新知讲解
解:设售价为每瓶x元时,日均毛利润为y元,由题意,得y=(x-9)(1360-80x)
= (10≤x≤14)
,在10≤x≤14的范围内.
当x=13时,
(元)
答:售价定为每瓶13元时,所得日均毛利润最大,最大日均毛利润为1280元。
新知讲解
求解最大利润问题的一般步骤
(1)建立利润与价格之间的函数关系式:
运用“总利润=总售价-总成本”或“总利润=单件利润
×销售量”
(2)结合实际意义,确定自变量的取值范围;
(3)在自变量的取值范围内确定最大利润:
可以利用配方法或公式求出最大利润;也可以画出函数的简图,利用简图和性质求出.
课堂练习
1.将进货单价为70元的某种商品按零售价100元一个售出时,每天能卖出20个;若这种商品在一定范围内每降价1元,每日销量就增加1个.为了获得最大利润,则应该降价( )
A.5元 B.10元 C.15元 D.20元
A
2.某旅行社在“五一”黄金周期间接团去外地旅游,经计算,所获营业额y(元)与旅行团人数x(人)满足关系式y=-x2+100x+28 400,要使所获营业额最大,则此旅行团应有( )
A.30人 B.40人 C.50人 D.55人
C
课堂练习
4.某种商品每件的进价为20元,调查表明:在某段时间内若以每件x元(20 ≤x ≤30)出售,可卖出(300-20x)件,使利润最大,则每件售价应定为 元.
25
3.某商品单个利润y(元)与变化的单价x(元)之间的关系为
y=-5x2+10x,当0.5≤x≤2时,最大利润是____元.
5
课堂练习
x
y
5
16
O
7
5. 某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系:
y=ax2+bx-75.其图象如图.
(1)销售单价为多少元时,该种商品每天的销售利润最大?最大利润是多少元?
解:(1)由题中条件可求y=-x2+20x-75
∵-1<0,对称轴x=10,
∴当x=10时,y值最大,最大值为25.
即销售单价定为10元时,销售利润最
大,为25元;
课堂练习
(2)销售单价在什么范围时,该种商品每天的销售利润不低于16元?
解:(2)由对称性知y=16时,x=7和13.
故销售单价在7 ≤x ≤13时,利润不低于16元.
5. 某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系:
y=ax2+bx-75.其图象如图.
x
y
5
16
O
7
课堂练习
6.某商家销售一款商品,进价每件80元,售价每件145元,每天销售40件,每销售一件需支付给商场管理费5元,未来一个月(按30天计算),这款商品将开展“每天降价1元”的促销活动,即从第一天开始每天的单价均比前一天降低1元,通过市场调查发现,该商品单价每降1元,每天销售量增加2件,设第x天(1≤x≤30且x为整数)的销售量为y件.
(1)直接写出y与x的函数关系式;
解:y=2x+40.
课堂练习
(2)设第x天的利润为w元,试求出w与x之间的函数关系式,并求出哪一天的利润最大,最大利润是多少元?
解:根据题意得w=(145-x-80-5)(2x+40)=-2x2+80x+2 400=-2(x-20)2+3 200,
∵-2<0,
∴函数有最大值,
∴当x=20时,w有最大值,为3 200,
∴第20天的利润最大,最大利润是3 200元.
课堂总结
最大利润问题
建立函数关系式
总利润=单件利润×销售量或总利润=总售价-总成本.
确定自变量取值范围
涨价:要保证销售量≥0;
降件:要保证单件利润≥0.
确定最大利润
利用配方法或公式求最大值或利用函数简图和性质求出.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
1.4.2二次函数的应用
浙教版 九年级上册
教学目标
知识目标:继续经历利用二次函数解决实际最值问题的过程.
能力目标:会综合运用二次函数和其他数学知识解决如有关距离等函数最值问题.
重点:利用二次函数的知识对现实问题进行数学地分析,即用数学的方式表示问题以及用数学的方法解决问题。
难点:将现实问题数学化,情景比较复杂。
新知导入
由于抛物线 y = ax 2 + bx + c 的顶点是最低(高)点,
当 时,二次函数 y = ax 2 + bx + c 有最小(大) 值
想一想:如何求出二次函数 y = ax 2 + bx + c 的最小(大)值?
新知讲解
例2、如图,B船位于A船正东26km处,现在A,B两船同时出发,A船以12km/h的速度朝正北方向行驶,B船以5km/h的速度朝正西方向行驶,何时两船相距最近?最近距离是多少?
新知讲解
解:设经过t(h)后,A,B两船分别到达A’,B’处,则
(t>0)
当13t-10=0,即时,有最小值576
所以当时,(km).
答:经过h,两船之间的距离最近,最近距离为24km.
新知讲解
例3、某超市销售一种饮料,每瓶进价为9元.经市场调查表明,当售价在10元到14元之间(含10元,14元)浮动时,每瓶售价每增加0.5元,日均销售量减少40瓶;当售价为每瓶12元时,日均销售量为400瓶.问销售价格定为每瓶多少元时,所得日均毛利润(每瓶毛利润=每瓶售价-每瓶进价)最大?最大日均毛利润为多少元?
新知讲解
解:设售价为每瓶x元时,日均毛利润为y元,由题意,得y=(x-9)(1360-80x)
= (10≤x≤14)
,在10≤x≤14的范围内.
当x=13时,
(元)
答:售价定为每瓶13元时,所得日均毛利润最大,最大日均毛利润为1280元。
新知讲解
求解最大利润问题的一般步骤
(1)建立利润与价格之间的函数关系式:
运用“总利润=总售价-总成本”或“总利润=单件利润
×销售量”
(2)结合实际意义,确定自变量的取值范围;
(3)在自变量的取值范围内确定最大利润:
可以利用配方法或公式求出最大利润;也可以画出函数的简图,利用简图和性质求出.
课堂练习
1.将进货单价为70元的某种商品按零售价100元一个售出时,每天能卖出20个;若这种商品在一定范围内每降价1元,每日销量就增加1个.为了获得最大利润,则应该降价( )
A.5元 B.10元 C.15元 D.20元
A
2.某旅行社在“五一”黄金周期间接团去外地旅游,经计算,所获营业额y(元)与旅行团人数x(人)满足关系式y=-x2+100x+28 400,要使所获营业额最大,则此旅行团应有( )
A.30人 B.40人 C.50人 D.55人
C
课堂练习
4.某种商品每件的进价为20元,调查表明:在某段时间内若以每件x元(20 ≤x ≤30)出售,可卖出(300-20x)件,使利润最大,则每件售价应定为 元.
25
3.某商品单个利润y(元)与变化的单价x(元)之间的关系为
y=-5x2+10x,当0.5≤x≤2时,最大利润是____元.
5
课堂练习
x
y
5
16
O
7
5. 某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系:
y=ax2+bx-75.其图象如图.
(1)销售单价为多少元时,该种商品每天的销售利润最大?最大利润是多少元?
解:(1)由题中条件可求y=-x2+20x-75
∵-1<0,对称轴x=10,
∴当x=10时,y值最大,最大值为25.
即销售单价定为10元时,销售利润最
大,为25元;
课堂练习
(2)销售单价在什么范围时,该种商品每天的销售利润不低于16元?
解:(2)由对称性知y=16时,x=7和13.
故销售单价在7 ≤x ≤13时,利润不低于16元.
5. 某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系:
y=ax2+bx-75.其图象如图.
x
y
5
16
O
7
课堂练习
6.某商家销售一款商品,进价每件80元,售价每件145元,每天销售40件,每销售一件需支付给商场管理费5元,未来一个月(按30天计算),这款商品将开展“每天降价1元”的促销活动,即从第一天开始每天的单价均比前一天降低1元,通过市场调查发现,该商品单价每降1元,每天销售量增加2件,设第x天(1≤x≤30且x为整数)的销售量为y件.
(1)直接写出y与x的函数关系式;
解:y=2x+40.
课堂练习
(2)设第x天的利润为w元,试求出w与x之间的函数关系式,并求出哪一天的利润最大,最大利润是多少元?
解:根据题意得w=(145-x-80-5)(2x+40)=-2x2+80x+2 400=-2(x-20)2+3 200,
∵-2<0,
∴函数有最大值,
∴当x=20时,w有最大值,为3 200,
∴第20天的利润最大,最大利润是3 200元.
课堂总结
最大利润问题
建立函数关系式
总利润=单件利润×销售量或总利润=总售价-总成本.
确定自变量取值范围
涨价:要保证销售量≥0;
降件:要保证单件利润≥0.
确定最大利润
利用配方法或公式求最大值或利用函数简图和性质求出.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
