1.4绝对值[上学期]

课件18张PPT。1．4 绝对值钟1．若点M在数轴原点的右边，则点M表示的数是___数，－3在数轴原点的 边，距离原点有____长度单位。2. 数轴上表示3和－3的点离开原点的距离是____ 。这两个点的位置关于原点_____.
3、（1）在数轴上标出下列各数：
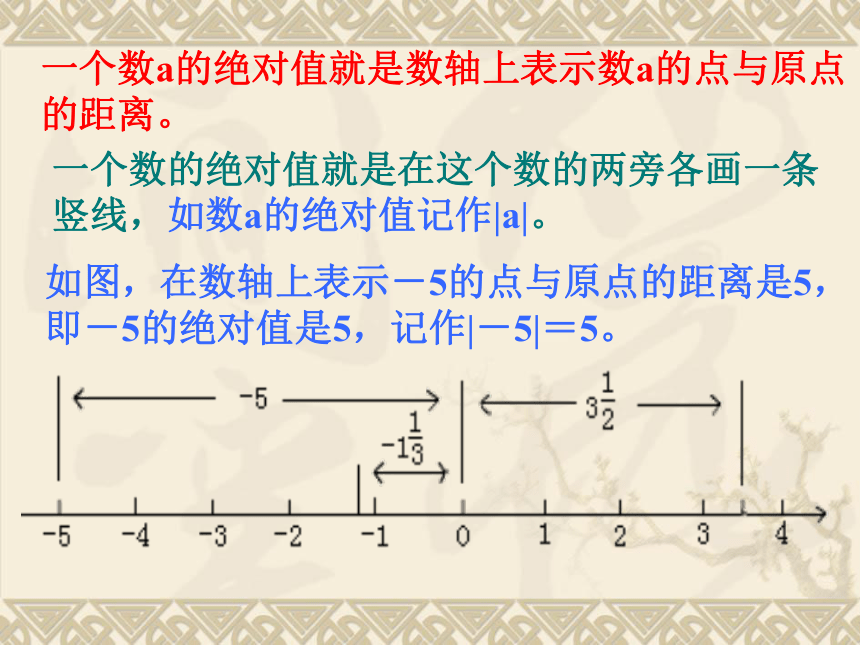
-3，4，0，-1.5，-4，3/2，2（2）有哪些数是互为相反数？从数轴上看，互为相反数有什么特点？ 我们发现，一对相反数虽然分别在原点两边， 但它们到原点的距离是相等的。如果我们不考虑这两点在原点的 哪一边，只考虑它们离开原点的距离，这个距离叫这两个数的绝对值一个数a的绝对值就是数轴上表示数a的点与原点的距离。 　　　　　　 一个数的绝对值就是在这个数的两旁各画一条竖线，如数a的绝对值记作|a|。 　　　　　　 如图，在数轴上表示－5的点与原点的距离是5，即－5的绝对值是5，记作|－5|＝5。　一个数的绝对值与这个数有什么关系？例如：|3|＝3，|＋7|＝7一个正数的绝对值是它本身例如：|－3|＝3，|－2.3|＝2.3一个负数的绝对值是它的相反数0的绝对值是0练习口答：求下列各式的值：
（1）｜-101 ｜ = ；
（2） ｜ 1+7/9 ｜ = ；
（3） ｜ 0 ｜ = ；
（4） ｜ -3.01 ｜ = ；
（5） ｜ +4 ｜ = ；
（6） ｜ -4 ｜ = 。 因为正数可用a＞0表示，负数可用a＜0表示，所以上述三条可表述成： 　　　　 (1)如果a＞0，那么|a|＝a 　　 (2)如果a＜0，那么|a|＝－a 　　 (3)如果a＝0，那么|a|＝0 　　　　　　 练：1、求下列各数的绝对值8，-8，1/4，-1/4，0，6，--3你有收获吗？ 2、 判断： (1)若一个数的绝对值是 2? ，则
这个数是2 。　　 (2)|5|＝|－5|。　　　(3)|－0.3|＝|0.3|。　　　　　　　　　　 (4)|3|＞0。　　　　 (5)|－1.4|＞0。　　　　　　　　　　　 (6)一个数的绝对值一定是正数。　　
(7)若a＝b，则|a|＝|b|。　　　　　　　　
(8)若|a|＝|b|，则a＝b。　　　　　　　 　
(9)若|a|＝－a，则a必为负数。　　　　 　 (10)绝对值相等,符号相反的两个数是互为相
反数。 3、
(1)绝对值是 ?的数有几个？各是什么？ (2)绝对值是0的数有几个？各是什么？ (3)有没有绝对值是－2的数？
4、计算： (1)|－15|－|6| 　　(2)|－0.24|＋|－5.06|
(3)|－3|×|－2|　　(4)|＋4|×|－5|
(5)|－12|÷|＋2| 　(6)|20|÷|－ ?| 　　　　　
5、(1)求绝对值不大于2的整数； (2)已知x是整数，且2.5＜|x|＜7，求x．2、已知有理数a在数轴上对应的点如图所示：则|a| =________ 4、如果a 的相反数是-0.74，那么|a| =______3. 如果一个数的绝对值等于3.25 ，则这个数是___小测验5、填空：
（1）符号是+号，绝对值是7的数是 ；
（2）符号是-号，绝对值是3的数是 。6、下列各数哪些是正数：
-2， | +1/3 | ， | -3 | ， | 0 | ，
- | +2 | ，-（-2），- | -2 |8、一个数的绝对值等于这个数本身，这个数是（ ）
A、零 B、正数 C、整数 D、正数和零
9、一个数的绝对值等于这个数的相反数，这个数是（ ）
A、零 B、负数
C、零或负数 D、非负数
10、下列判断中正确的是（ ）
A、任何有理数的绝对值都是正数
B、任何有理数的绝对值都不是负数
C、绝对值相等的数一定相等
D、不相等的两个有理数，它们的绝对
值一定不相等1、绝对值等于3的有理数是 。
2、到-4的距离等于3的数是多少？思考