【专题训练】二次函数实际应用(追击相遇)(含解析)
文档属性
| 名称 | 【专题训练】二次函数实际应用(追击相遇)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-10 06:06:20 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
二次函数实际应用(追击相遇)
一、填空题(共13题;共13分)
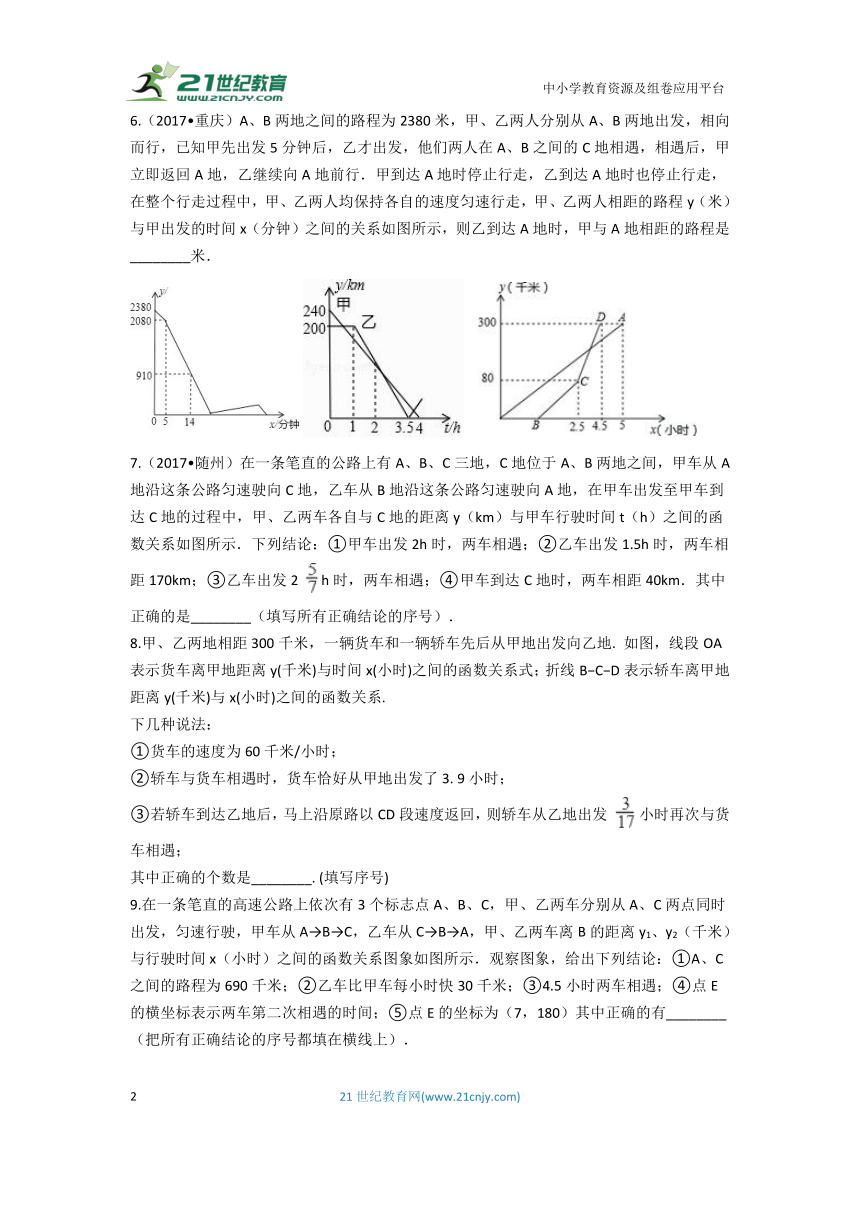
1.甲、乙两人从A地出发前往B地,甲先出发1分钟后,乙再出发,乙出发一段时间后返回A地取物品,甲、乙两人同时达到B地和A地,并立即掉头相向而行直至相遇,甲、乙两人之间相距的路程y(米)与甲出发的时间x(分钟)之间的关系如图所示,则甲、乙两人最后相遇时,乙距B地的路程是________米.
2.一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后分别按原速同时驶往甲地,两车之间的距离S(km)与慢车行驶时间t(h)之间的函数图象如图所示,则快车到达甲地时,慢车距离甲地________ km.
3.周末小明和爸爸从家里出发到野外郊游,小明骑自行车出发0.3小时后爸爸开始骑摩托车追赶,爸爸在追上小明前停留了0.1小时与碰到的朋友聊天,聊天完毕后以原来的速度继续追赶.在整个过程中,他们离家的路程y(千米)与爸爸出发的时间x(小时)之间的关系如图所示,则爸爸出发________小时后与小明相遇.
4.已知A地在C、B两地之间,甲乙两人分别从A、B两地同时出发,相向而行,经过一段时间后相遇,甲继续向B地前进,乙继续向A地前进;甲到达B地后立即返回,在C地甲追上乙.甲乙两人相距的路程y(米)与出发的时间x(分钟)之间的关系如图所示,则A、C两地相距________米.
5.甲、乙两人在1800米长的直线道路上跑步,甲、乙两人同起点、同方向出发,并分别以不同的速度匀速前进.已知,甲出发30秒后,乙出发,乙到终点后立即返回,并以原来的速度前进,最后与甲相遇,此时跑步结束.如图,y(米)表示甲、乙两人之间的距离,t(秒)表示甲出发的时间,图中折线及数据表示整个跑步过程中y与t函数关系.那么,乙到终点后________秒与甲相遇.
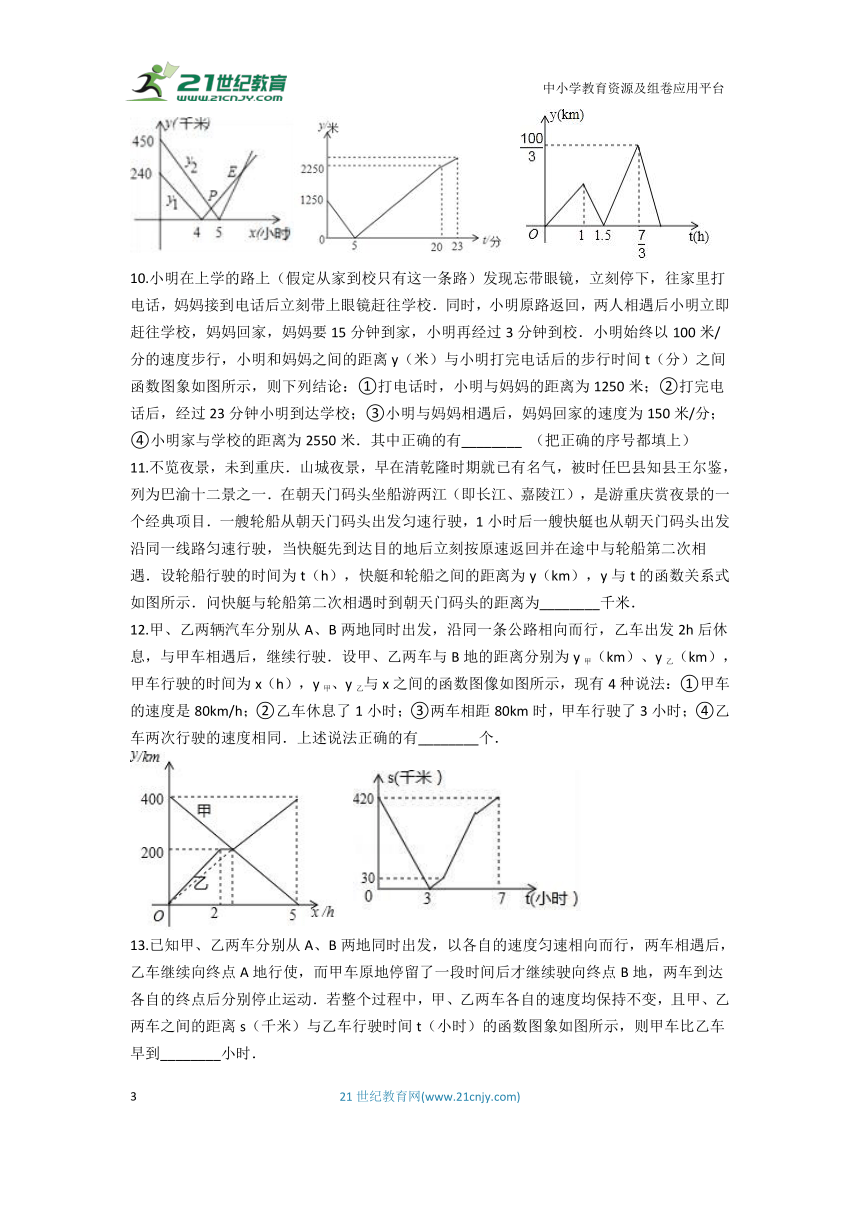
6.(2017 重庆)A、B两地之间的路程为2380米,甲、乙两人分别从A、B两地出发,相向而行,已知甲先出发5分钟后,乙才出发,他们两人在A、B之间的C地相遇,相遇后,甲立即返回A地,乙继续向A地前行.甲到达A地时停止行走,乙到达A地时也停止行走,在整个行走过程中,甲、乙两人均保持各自的速度匀速行走,甲、乙两人相距的路程y(米)与甲出发的时间x(分钟)之间的关系如图所示,则乙到达A地时,甲与A地相距的路程是________米.
7.(2017 随州)在一条笔直的公路上有A、B、C三地,C地位于A、B两地之间,甲车从A地沿这条公路匀速驶向C地,乙车从B地沿这条公路匀速驶向A地,在甲车出发至甲车到达C地的过程中,甲、乙两车各自与C地的距离y(km)与甲车行驶时间t(h)之间的函数关系如图所示.下列结论:①甲车出发2h时,两车相遇;②乙车出发1.5h时,两车相距170km;③乙车出发2 h时,两车相遇;④甲车到达C地时,两车相距40km.其中正确的是________(填写所有正确结论的序号).
8.甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地. 如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系式;折线B C D表示轿车离甲地距离y(千米)与x(小时)之间的函数关系.
下几种说法:
①货车的速度为60千米/小时;
②轿车与货车相遇时,货车恰好从甲地出发了3. 9小时;
③若轿车到达乙地后,马上沿原路以CD段速度返回,则轿车从乙地出发 小时再次与货车相遇;
其中正确的个数是________. (填写序号)
9.在一条笔直的高速公路上依次有3个标志点A、B、C,甲、乙两车分别从A、C两点同时出发,匀速行驶,甲车从A→B→C,乙车从C→B→A,甲、乙两车离B的距离y1、y2(千米)与行驶时间x(小时)之间的函数关系图象如图所示.观察图象,给出下列结论:①A、C之间的路程为690千米;②乙车比甲车每小时快30千米;③4.5小时两车相遇;④点E的横坐标表示两车第二次相遇的时间;⑤点E的坐标为(7,180)其中正确的有________(把所有正确结论的序号都填在横线上).
10.小明在上学的路上(假定从家到校只有这一条路)发现忘带眼镜,立刻停下,往家里打电话,妈妈接到电话后立刻带上眼镜赶往学校.同时,小明原路返回,两人相遇后小明立即赶往学校,妈妈回家,妈妈要15分钟到家,小明再经过3分钟到校.小明始终以100米/分的速度步行,小明和妈妈之间的距离y(米)与小明打完电话后的步行时间t(分)之间函数图象如图所示,则下列结论:①打电话时,小明与妈妈的距离为1250米;②打完电话后,经过23分钟小明到达学校;③小明与妈妈相遇后,妈妈回家的速度为150米/分;④小明家与学校的距离为2550米.其中正确的有________ (把正确的序号都填上)
11.不览夜景,未到重庆.山城夜景,早在清乾隆时期就已有名气,被时任巴县知县王尔鉴,列为巴渝十二景之一.在朝天门码头坐船游两江(即长江、嘉陵江),是游重庆赏夜景的一个经典项目.一艘轮船从朝天门码头出发匀速行驶,1小时后一艘快艇也从朝天门码头出发沿同一线路匀速行驶,当快艇先到达目的地后立刻按原速返回并在途中与轮船第二次相遇.设轮船行驶的时间为t(h),快艇和轮船之间的距离为y(km),y与t的函数关系式如图所示.问快艇与轮船第二次相遇时到朝天门码头的距离为________千米.
12.甲、乙两辆汽车分别从A、B两地同时出发,沿同一条公路相向而行,乙车出发2h后休息,与甲车相遇后,继续行驶.设甲、乙两车与B地的距离分别为y甲(km)、y乙(km),甲车行驶的时间为x(h),y甲、y乙与x之间的函数图像如图所示,现有4种说法:①甲车的速度是80km/h;②乙车休息了1小时;③两车相距80km时,甲车行驶了3小时;④乙车两次行驶的速度相同.上述说法正确的有________个.
13.已知甲、乙两车分别从A、B两地同时出发,以各自的速度匀速相向而行,两车相遇后,乙车继续向终点A地行使,而甲车原地停留了一段时间后才继续驶向终点B地,两车到达各自的终点后分别停止运动.若整个过程中,甲、乙两车各自的速度均保持不变,且甲、乙两车之间的距离s(千米)与乙车行驶时间t(小时)的函数图象如图所示,则甲车比乙车早到________小时.
二、综合题(共8题;共84分)
14.如图,王爷爷家院子里有一块三角形田地ABC,AB=AC=5米,BC=6米,现打算把它开垦出一个矩形MNFE区域种植韭菜,△AMN区域种植芹菜,△CME和△BNF区域种植青菜(开垦土地面积损耗均忽略不计),其中点M,N分别在AC,AB上,点E,F在BC上,已知韭菜每平方米收益100元,芹菜每平方米收益60元,青菜每平方米收益40元,设CM=5x米,王爷爷的蔬菜总收益为W元.
(1)当矩形MNFE恰好为正方形时,求韭菜种植区域矩形MNFE的面积.
(2)若种植韭菜的收益等于另两种蔬菜收益之和的2倍,求这时x的值.
(3)求王爷爷的蔬菜总收益为W关于x的函数表达式及W的最大值.
15.某商场销售一种成本为每件30元的商品,销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似看作一次函数y=-10x+600,商场销售该商品每月获得利润为w(元).
(1)求w与x之间的函数关系式;
(2)如果商场销售该商品每月想要获得2000元的利润,那么每月成本至少多少元?
(3)为了保护环境,政府部门要求用更加环保的新产品替代该商品,商场销售新产品,每月的销量与销售价格之间的关系与原产品的销售情况相同,新产品的成本每件32元,若新产品每月的销售量不低于200件时,政府部门给予每件4元的补贴,试求定价多少元时,每月销售新产品的利润最大?求出最大的利润。
16.为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.李明按照相关政策投资销售本市生产的一种新型节能灯.已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=-10x+500 .
(1)李明在开始创业的第一个月将销售单价定为20元,那么政府这个月为他承担的总差价为多少元
(2)设李明获得的利润为W(元),当销售单价定为多少元时,每月可获得最大利润
(3)物价部门规定,这种节能灯的销售单价不得高于25元.如果李明想要每月获得的利润不低于3000元,那么政府为他承担的总差价最少为多少元
17.为了解都匀市交通拥堵情况,经统计分析,都匀彩虹桥上的车流速度v(千米/小时)是车流密度x(辆/千米)的函数,当桥上的车流密度达到220辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度为20辆/千米时,车流速度为80千米/小时.研究表明:当20≤x≤220时,车流速度v是车流密度x的一次函数.
(1)求彩虹桥上车流密度为100辆/千米时的车流速度;
(2)在交通高峰时段,为使彩虹桥上车流速度大于40千米/小时且小于60千米/小时,应控制彩虹桥上的车流密度在什么范围内?
(3)当车流量(辆/小时)是单位时间内通过桥上某观测点的车辆数,即:车流量=车流速度×车流密度.当20≤x≤220时,求彩虹桥上车流量y的最大值.
18.为节约用水,某市居民生活用水按阶梯式水价计量,水价分为三个阶梯,价格表如下表所示:
某市自来水销售价格表
类别 月用水量 (立方米) 供水价格 (元/立方米) 污水处理费 (元/立方米)
居民生活用水 阶梯一 0~18(含18) 1.90 1.00
阶梯二 18~25(含25) 2.85
阶梯三 25以上 5.70
(注:居民生活用水水价=供水价格+污水处理费)
(1)当居民月用水量在18立方米及以下时,水价是________元/立方米.
(2)4月份小明家用水量为20立方米,应付水费为:
18×(1.90+1.00)+2×(2.85+1.00)=59.90(元)
预计6月份小明家的用水量将达到30立方米,请计算小明家6月份的水费.
(3)为了节省开支,小明家决定每月用水的费用不超过家庭收入的1%,已知小明家的平均月收入为7530元,请你为小明家每月用水量提出建议
19.为响应荆州市“创建全国文明城市”号召,某单位不断美化环境,拟在一块矩形空地上修建绿色植物园,其中一边靠墙,可利用的墙长不超过18m,另外三边由36m长的栅栏围成.设矩形ABCD空地中,垂直于墙的边AB=xm,面积为ym2(如图).
甲 乙 丙
单价(元/棵) 14 16 28
合理用地(m2/棵) 0.4 1 0.4
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)若矩形空地的面积为160m2 , 求x的值;
(3)若该单位用8600元购买了甲、乙、丙三种绿色植物共400棵(每种植物的单价和每棵栽种的合理用地面积如下表).问丙种植物最多可以购买多少棵?此时,这批植物可以全部栽种到这块空地上吗?请说明理由.
20.某公司计划从甲、乙两种产品中选择一种生产并销售,每年产销 x 件,已知产销两种产品的有关信息 如下:
产品 每件售价/万元 每件成本/万元 年最大产销量/件
甲 6 3 200
乙 20 10 80
甲、乙两产品每年的其他费用与产销量的关系分别是: y1 = kx + b 和 y2 =ax2+ m ,它们的函数图象分别如图(1)和图(2)所示.
(1)求: y1 、 y2 的函数解析式;
(2)分别求出产销两种产品的最大利润;(利润=销售额-成本-其它费用)
(3)若通过技术改进,甲产品的每件成本降到 a 万元,乙产品的年最大产销量可以达到 110 件,其它都不变,为获得最大利润,该公式应该选择产销哪种产品?请说明理由.
21.嘉兴某公司抓住“一带一路”的机遇不断创新发展,生产销售某产品.该产品销售量y(万件)与售价x(元/件)之间存在图1(一条线段)所示的变化趋势,总成本P(万元)与销售量y(万件)之间存在图2所示的变化趋势,当6≤y≤10时可看成一条线段,当10≤y≤18时可看成抛物线P=- y2+8y+m.
(1)写出y与x之间的函数关系式;
(2)若销售量不超过10万件时,利润为45万元,求此时的售价为多少元/件
(3)当售价为多少元时,利润最大,最大值是多少万元 (利润=销售总额-总成本)
答案解析部分
一、填空题
1.【答案】320
【解析】【解答】由图象可知甲的速度为:80÷1=80(米/分),
乙的速度为:80-(140-80)÷(4-1)=60(米/分),
由于乙后出发,出发3分钟后返回A地,甲、乙两人同时达到B地和A地,所以甲从A地到B地共用时4+3=7(分),
A、B两地相距80×7=560米,
560÷(80+60)=4,
所以甲、乙两人最后相遇时,乙距B地的路程是560-60×4=320(米),
故答案为:320.
【分析】根据图像求出甲乙的速度,再求出甲从A地到B地共用的时间,及A、B两地的路程,然后求出甲、乙两人最后相遇时,乙距B地的路程即可。
2.【答案】60
【解析】【解答】解:快车的速度为560÷7=80(km/h), 慢车的速度为560÷4﹣80=60(km/h),
快车到达甲地时,慢车距离甲地的距离为(80﹣60)×(7﹣4)=60(km).
故答案为:60.
【分析】根据速度=路程÷时间,即可求出快车的速度,由慢车速度=两地间的距离÷两车相遇时间﹣快车速度,即可求出慢车的速度,再根据路程=两车速度之差×行驶时间即可得出结论.
3.【答案】0.7
【解析】【解答】解:爸爸的速度为36÷(1﹣0.1)=40(千米/小时),
小明的速度为36÷(1.2+0.3)=24(千米/小时).
设爸爸出发t小时后与小明相遇,此时,小明出发了(t+0.3)小时,
根据题意得:40(t﹣0.1)=24(t+0.3),
解得:t=0.7.
答:爸爸出发0.7小时后与小明相遇.
故答案为:0.7.
【分析】由图像可求出二人速度,根据相遇时二人距离家的路程相等列出方程40(t﹣0.1)=24(t+0.3),可求出时间.
4.【答案】 450
【解析】【解答】解:甲乙两人的速度和为450÷3=150(米/分钟),
甲的速度为450÷5=90(米/分钟),
乙的速度为150﹣90=60(米/分钟),
设A、C两地相距m米,则B、C两地相距(m+450)米,
根据题意得: ,
解得:m=450,
故答案为:450.
【分析】根据题意可以求出甲和乙的速度之和,甲和乙二人各自的速度。根据二人在过程中所用的时间相同,即可列出等量关系式,求出m的值。
5.【答案】
【解析】【解答】解:甲的速度为90÷30=3(米/秒), 乙的速度为3+90÷(120﹣30)=4(米/秒).
乙到达终点时,甲出发的时间为1800÷4+30=480(秒),
此时甲离终点的距离为1800﹣3×480=360(米),
乙返回后与甲相遇的时间为360÷(3+4)= (秒).
故答案为: .
【分析】根据速度=路程÷时间可求出甲的速度,由乙的速度=甲的速度+二者速度差可求出乙的速度,利用时间=路程÷速度可求出乙到达终点的时间,结合路程=速度×时间可求出此时甲离终点的距离,再根据相遇所需时间=甲离终点的距离÷甲、乙速度和,即可得出结论.
6.【答案】180
【解析】【解答】解:由题意可得, 甲的速度为:(2380﹣2080)÷5=60米/分,
乙的速度为:(2080﹣910)÷(14﹣5)﹣60=70米/分,
则乙从B到A地用的时间为:2380÷70=34分钟,
他们相遇的时间为:2080÷(60+70)=16分钟,
∴甲从开始到停止用的时间为:(16+5)×2=42分钟,
∴乙到达A地时,甲与A地相距的路程是:60×(42﹣34﹣5)=60×3=180米,
故答案为:180.
【分析】根据题意和函数图象中的数据可以求得甲乙的速度和各段用的时间,从而可以求得乙到达A地时,甲与A地相距的路程.
7.【答案】②③④
【解析】【解答】解:①观察函数图象可知,当t=2时,两函数图象相交, ∵C地位于A、B两地之间,
∴交点代表了两车离C地的距离相等,并不是两车相遇,结论①错误;
②甲车的速度为240÷4=60(km/h),
乙车的速度为200÷(3.5﹣1)=80(km/h),
∵(240+200﹣60﹣170)÷(60+80)=1.5(h),
∴乙车出发1.5h时,两车相距170km,结论②正确;
③∵(240+200﹣60)÷(60+80)=2 (h),
∴乙车出发2 h时,两车相遇,结论③正确;
④∵80×(4﹣3.5)=40(km),
∴甲车到达C地时,两车相距40km,结论④正确.
综上所述,正确的结论有:②③④.
故答案为:②③④.
【分析】①观察函数图象可知,当t=2时,两函数图象相交,结合交点代表的意义,即可得出结论①错误;②根据速度=路程÷时间分别求出甲、乙两车的速度,再根据时间=路程÷速度和可求出乙车出发1.5h时,两车相距170km,结论②正确;③根据时间=路程÷速度和可求出乙车出发2 h时,两车相遇,结论③正确;④结合函数图象可知当甲到C地时,乙车离开C地0.5小时,根据路程=速度×时间,即可得出结论④正确.综上即可得出结论.
8.【答案】 ①②③
【解析】【解答】由图象可知:货车是匀速行驶,速度=300÷5=60千米/小时,故①正确;
设线段DC的解析式是y=kx+b,
根据题意得:
解得: ,
则线段DC的解析式是:y=110x-195(2.5≤x≤4.5)
设OA的解析式是:y=mx,
根据题意得:5m=300,
解得:m=60,
则函数解析式是:y=60x,
根据题意得:
解得: ,
则轿车与货车相遇时,货车恰好从甲地出发了3.9小时,故②正确;
设轿车从乙地出发x小时再次与货车相遇,
∵V货车=60千米/时,CD段V轿车= (千米/时),
∴110x+60(x+4.5)=300,
解得x= (小时),故③正确.
故答案是:①②③.
【分析】 ①根据图象提供的信息解决问题,横轴代表的是货车从甲地去乙地的行驶时间,纵轴代表的是货车离甲的距离,由A点(5,300)可知甲乙两地相距300千米,货车行驶了5小时,根据速度等于路程除以时间即可算出货车的速度,②只要找出线段OA与CD交点的横坐标即可判断出②是否正确,利用待定系数法求出线段CD,OA的解析式,再解两解析式组成的方程组,即可求出其交点坐标,进而得出结论;③首先根据路程除以时间等于速度,算出轿车行驶CD段的速度, 若轿车到达乙地后,马上沿原路以CD段速度返回, 则轿车与货车实际是一个相遇问题,设轿车从乙地出发x小时再次与货车相遇,根据货车所走的路程+轿车所走的路程等于甲乙两地的全程即可列出方程,求解即可判断③的正确与否。
9.【答案】①②⑤
【解析】【解答】①450+240=690(千米).
故A、C之间的路程为690千米是正确的;
②450÷5-240÷4
=90-60
=30(千米/小时).
故乙车比甲车每小时快30千米是正确的;
③690÷(450÷5+240÷4)
=690÷(90+60)
=690÷150
=4.6(小时).
故4.6小时两车相遇,原来的说法是错误的;
⑤(450-240)÷(450÷5-240÷4)
=210÷(90-60)
=210÷30
=7(小时),
450÷5×7-450
=630-450
=180(千米).
故点E的坐标为(7,180)是正确的,
故其中正确的有①②⑤.
故答案为:①②⑤.
【分析】①抓住已知条件:甲、乙两车分别从A、C两点同时出发,由450+240计算即可求解; ②根据速度=路程÷时间求出两车的速度,再相减即可求解; ③根据相遇时间=路程和÷速度和路程算式计算即可求解; ④根据时间=路程差÷速度差求解即可.
10.【答案】①②④
【解析】【解答】解:①当t=0时,y=1250,
∴打电话时,小明与妈妈的距离为1250米,①正确;
②∵23﹣0=23(分钟),
∴打完电话后,经过23分钟小明到达学校,②正确;
③妈妈来学校的速度为:1250÷5﹣100=150(米/分),
二者相遇时,离家的距离为:150×5=750(米),
妈妈回家的速度为:750÷15=50(米/分),
∴③不正确;
④小明家与学校的距离为750+(23﹣5)×100=2550(米),
∴④正确.
综上可知:其中正确的结论有①②④.
故答案为:①②④.
【分析】①根据函数图象可知,当t=0时,y=1250,从而得出①正确;②结合函数图象可得知,小明打完电话后23分钟到校,从而得出②正确;③根据“妈妈来学校的速度=二者间的距离÷时间﹣小明的速度”代入数据即可得出妈妈赶往学校的速度,再依据“妈妈离家的距离=妈妈赶往学校的速度×时间”即可得出二者相遇时,妈妈离家的距离,最后由“妈妈回家的速度=离家的距离÷时间”即可得出结论,从而得出③不正确;④根据“小明家离学校的距离=二者相遇时离家的距离+小明的速度×相遇后小明赶到学校的时间”代入数据即可得知④成立.综上即可得出结论.
11.【答案】55
【解析】【解答】解:如图,轮船2小时后在A处,1.5小时后在B处相遇, 小时后快艇到达目的地C,设再过x小时在D处相遇,设轮船是速度为akm/h,快艇的速度为bkm/h.
由题意0.5(b﹣a)=a,解得b=3a,
由题意( ﹣ )(3a﹣a)= ,
解得a=20,
由题意x(3a+a)= ,
∴x= ,
( + )×20=55,
∴快艇与轮船第二次相遇时到朝天门码头的距离55km.
故答案为55.
【分析】如图,轮船2小时后在A处,1.5小时后在B处相遇, 小时后快艇到达目的地C,设再过x小时在D处相遇,设轮船是速度为akm/h,快艇的速度为bkm/h.列出方程求出a的值,再求出x的值,即可解决问题.
12.【答案】1
【解析】【解答】解:由图像可得, 甲车的速度为:400÷5=80km/h,故①正确,
甲车与乙车相遇时,甲车行驶的时间为:(400﹣200)÷80=2.5h,
∴乙车休息的时间为2.5﹣2=0.5h,故②错误,
由图像可知,两车相距80km,存在两种情况,故③错误,
乙车休息前行驶的速度为:200÷2=100km/h,乙车休息后行驶的速度为:(400﹣200)÷(5﹣2.5)=80km/h,
∵100≠80,故④错误,
故答案为:1.
【分析】根据题意和函数图像可以判断题目中的各个小题是否正确,从而可以解答本题.
13.【答案】
【解析】【解答】解:由题意乙的速度= =60千米/小时,
甲的速度= =80千米/小时,
甲从A到B需要 = 小时,
中途休息了 = 小时,
∴甲时间行驶时间= + = 小时,
7﹣ = ,
∴甲车比乙车早到 小时.
故答案为: .
【分析】根据图像,根据图像提供的信息,先求出甲乙的速度,再分别求出甲从A到B的时间及中途休息的时间,甲行驶的时间,然后求出甲车比乙车早到的时间。
二、综合题
14.【答案】 (1)解:作AH⊥BC于H,交MN于D.
∵AB=AC,AH⊥BC,
∴CH=HB=3,
在Rt△ACH中,AH= =4,
∵ME∥AH,
∴ = = ,
∴CE=3x,EM=EF=4x,
易证△MEC≌△NFB,
∴CE=BF=3x,
∴3x+4x+3x=6,
∴x= ,
∴EM= ,
∴矩形MNFE的面积为 平方米
(2)解:由题意:100×4x (6﹣6x)=2 [60× ×(6﹣6x) (4﹣4x)+40×4x×3x],
解得x= 或
(3)解:由题意W=100×4x (6﹣6x)+60× ×(6﹣6x) (4﹣4x)+40×4x×3x=﹣1200x2+960x+720=﹣1200(x﹣ )2+912,
, ∵﹣1200<0,
∴x= 时,W有最大值,最大值为912元.
【解析】【分析】(1)作AH⊥BC于H,交MN于D,利用勾股定理求出AH的长,再根据平行得线段成比例,设 CE=3x,EM=EF=4x, 结合已知条件易证△MEC≌△NFB,就可得出CE=BF=3x,然后根据BC=6,列方程求解即可。
(2)此题的等量关系是: 种植韭菜的收益=另两种蔬菜收益之和×2,设未知数,列方程求解即可。
(3)根据题意列出W与x的函数解析式,再将函数解析式转化为顶点式,利用二次函数的性质,就可求出W的最大值。
15.【答案】(1)解:w=(x﹣30)(﹣10x+600)=﹣10x2+900x﹣18000
(2)解:由题意得,﹣10x2+900x﹣18000=2000,解得:x1=40,x2=50,当x=40时,成本为30×(﹣10×40+600)=6000(元),当x=50时,成本为30×(﹣10×50+600)=3000(元),∴每月想要获得2000元的利润,每月成本至少3000元
(3)解:当y<200时,即:﹣10x+600<200,解得:x>40,w=(x﹣32)(﹣10x+600)=﹣10(x﹣46)2+1960,∵a=﹣10<0,x>40,∴当x=46时,w最大值=1960(元);
当y≥200时,即:﹣10x+600≥200,解得:x≤40,w=(x﹣32+4)(﹣10x+600)=﹣10(x﹣44)2+2560,∵a=﹣10<0,∴抛物线开口向下,当32<x≤40时,w随x的增大而增大,∴当x=40时,w最大值=2400(元),∵1960<2400,∴当x=40时,w最大.
答:定价每件40元时,每月销售新产品的利润最大,最大利润为2400元.
【解析】【分析】(1)利用利润法则:单件利润销量=利润,可列出函数表达式;(2)根据函数关系式的特殊值,列出方程,解方程求出结果;(3)根据销量进行分类讨论,分别列出分段函数,在自变量的取值范围内,根据二次函数的单调性,求出最值.
16.【答案】(1)解:在y=-10x+500中,x=20 y=300300(12-10)=600 承担总差价为600元
(2)解:W=(-10x+500)(x-10)=-10(x-30)2+4000x=30时,W有最大值4000
(3)解:W=-10(x-30) +4000 令W≥3000 画出草图, 由图像可知 有20≤x≤40 ∵x≤25 ∴20≤x≤25 在y=-10x+500中,-10<0 ∴y随x的增大而减小 ∴x=25时,y最小为250 ∴政府为他承担总差价最少为250(12-10)=500元
【解析】【分析】(1)将x=20代入y=-10x+500,求出y的值,利用成本价和出厂价,可列式计算求出结果。
(2)利用李明获得的利润为W=每一件的利润×销售量,列出W与x的函数解析式,将其函数解析式转化为顶点式,利用二次函数的性质求解。
(3)结合函数图形,根据已知条件, 就可求出销售单价不得高于25元 且每月获得的利润不低于3000元 时, 政府为他承担的总差价。
17.【答案】(1)解:设车流速度v与车流密度x的函数关系式为v=kx+b,由题意,得
,
解得: ,
∴当20≤x≤220时,v=﹣ x+88,
当x=100时,v=﹣ ×100+88=48(千米/小时)
(2)解:由题意,得
,
解得:70<x<120,
∴应控制大桥上的车流密度在70<x<120范围内
(3)解:设车流量y与x之间的关系式为y=vx,
当20≤x≤220时,
y=(﹣ x+88)x=﹣ (x﹣110)2+4840,
∴当x=110时,y最大=4840,
∵4840>1600,
∴当车流密度是110辆/千米,车流量y取得最大值是每小时4840辆
【解析】【分析】(1)用待定系数法求一次函数解析式。(2)利用不等式组求不等式组解集。(3)利用车流量=车流速度×车流密度关系式列出二次函数解析式配方为顶点式,求最值.
18.【答案】(1)1.90
(2)解:由题意可得:
小明家6月份的水费是:(1.9+1)×18+(2.85+1)×7+(5.70+1)×5=112.65(元)
(3)解:由题意可知,当用水量为18立方米时,应交水费52.2元,当用水量为25立方米时,应交水费79.15元,而小明家计划的水费不超过75.3元,由此可知他们家的用水量不超过18立方米,而不足25立方米,设他们家的用水量为x立方米,则由题意可得:
18×(1.9+1)+(x-18)×(2.85+1) 75.3,解得:x 24,
∴当小明家每月的用水量不要超过24立方米时,水费就不会超过他们家庭总收入的1%.
【解析】【解答】解:(1)由表中数据可知,当用水量在18立方米及以下时,水价为1.9元/立方米;
【分析】(1)由 某市自来水销售价格表中的信息可知, 当居民月用水量在18立方米及以下时,水价 为 1.90 元/立方米 ;
(2) 4月份小明家用水量为20立方米,属于表格中的第二阶梯,所以应付水费为两部分: 18立方米及以下时,水价 按(1.90+1)元/立方米计算,超过部分按( 2.85+1.00 )元/立方米计算,再把两部分相加即可求解;
6月份小明家的用水量将达到30立方米, 则按阶梯三计算:18立方米及以下时,水价 按(1.90+1)元/立方米计算,超过部分按( 2.85+1.00 )元/立方米计算,超过25以上的按( 5.70+1 )元/立方米计算,再把这三部分相加即可求解;
(3)由题意根据小明家的平均月收入为7530元 可计算出小明家计划的水费不超过75.3元, 列出不等式即可求解。
19.【答案】 (1)解:y=x(36﹣2x)=﹣2x2+36x(9≤x<18)
(2)解:由题意:﹣2x2+36x=160,
解得x=10或8.
∵x=8时,36﹣16=20>18,不符合题意,
∴x的值为10.
(3)解:∵y=﹣2x2+36x=﹣2(x﹣9)2+162,
∴x=9时,y有最大值162,
设购买了乙种绿色植物a棵,购买了丙种绿色植物b棵,
由题意:14(400﹣a﹣b)+16a+28b=8600,
∴a+7b=1500,
∴b的最大值为214,此时a=2,
需要种植的面积=0.4×(400﹣214﹣2)+1×2+0.4×214=161.2<162,
∴这批植物可以全部栽种到这块空地上.
【解析】【分析】(1)先用含x的代数式表示出BC的长为(36-2x),然后根据矩形的面积公式计算即可。最后根据各边长大于0和BC的长不超过墙长列出不等式组,解之求出x的取值范围。
(2)当y=160时得 -2x2+36x=160, 解方程求得x的值,注意检验x的值是否符合题意(在取值范围内)。
(3)先根据二次函数的性质求出面积的最大值;又设购买了乙种绿色植物a棵,购买了丙种绿色植物b棵,根据购买总费列出方程,从而求得b的最大整数值为214,此时a=2,然后求出此时的种植面积,由此时的种植面积小于空地的最大面积判断出这批植物可以全部栽种到这块空地上.
20.【答案】 (1)解:依题意得: ,所以 ,所以, ;
由已知可得: ,所以, ,所以, .
(2)解: , ( ),
2>0, ,
∴x=200时, .
,( ).
, 时,
∴x=80时,
(3)解: , ,
, ,
∴x=200时, ,
, ,
∴x=100时, ,
① ,解得 ,
当 时,选择两种产品一样.
② 解得 ,
当 时,选择甲产品.
③ ,解得
当 时,选择乙产品.
, (1) , ;(2)x=200时, ,x=80时, ;
【解析】【分析】(1)观察函数图像可知:直线y1经过点(0,10),(200,210),直线y1经过点(0,40),(80,360),利用待定系数法,分别求出两函数解析式即可。
(2)根据总利润=(每一件的售价-每一件的成本价)×数量-y,分别列出函数解析式,根据自变量的取值范围及一次函数和二次函数的性质,就可求出产销两种产品的最大利润 。
(3)由题意可知,甲产品的售价为a元,根据甲的总利润W1=(每一件的售价-每一件的成本价)×数量-y1 , 再列出W2与x的函数关系式,利用二次函数的性质,可求出最大利润时x的值;再分情况讨论:W1=460;W1>460;W1<460;分别求出a的取值范围,即可解答此题。
21.【答案】 (1)解:设y=kx+b,把(6,18),(18,6)代入得
解得
∴y=-x+24
(2)解:当6≤y≤10时,可得14≤x≤18,
x(-x+24)-10y=45,
即-x2+34x-240=45
解得x=15或x=19(舍去)
∴此时售价为15元/件。
(3)解:把(10,100)代入P= y2+8y+m得到m=40
∴P= y2+8y+40
①当6≤x≤10时,10≤y≤18,
w=x(-x+24)-( y2+8y+40)= (x-14)2+40
∴当x=14时,w最大值为40万元
②当14≤x≤18时,6≤y≤10,
W=x(-x+24)-10y=-(x-17)2+49
∴当x=17时,w最大值为49万元。
∴综上所述,当x=17时w最大值为49万元。
【解析】【分析】(1)观察图像,将 点(6,18)和点(18,6)代入 y=kx+b ,就可求出y与x的函数解析式。
(2)根据当6≤y≤10时,可求出x的取值范围为14≤x≤18,再根据销售量不超过10万件时,利润为45万元,建立关于x的方程,解方程求出符合题意的x的值,即可求解。
(3)将点(10,100)代入 P= y2+8y+m,可求出m的值,即可得出p与y的函数解析式,再分情况讨论: ①当6≤x≤10时,10≤y≤18;②当14≤x≤18时,6≤y≤10,分别列出W与x的函数解析式,利用二次函数的性质解答即可。
21世纪教育网(www.21cnjy.com)
二次函数实际应用(追击相遇)
一、填空题(共13题;共13分)
1.甲、乙两人从A地出发前往B地,甲先出发1分钟后,乙再出发,乙出发一段时间后返回A地取物品,甲、乙两人同时达到B地和A地,并立即掉头相向而行直至相遇,甲、乙两人之间相距的路程y(米)与甲出发的时间x(分钟)之间的关系如图所示,则甲、乙两人最后相遇时,乙距B地的路程是________米.
2.一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后分别按原速同时驶往甲地,两车之间的距离S(km)与慢车行驶时间t(h)之间的函数图象如图所示,则快车到达甲地时,慢车距离甲地________ km.
3.周末小明和爸爸从家里出发到野外郊游,小明骑自行车出发0.3小时后爸爸开始骑摩托车追赶,爸爸在追上小明前停留了0.1小时与碰到的朋友聊天,聊天完毕后以原来的速度继续追赶.在整个过程中,他们离家的路程y(千米)与爸爸出发的时间x(小时)之间的关系如图所示,则爸爸出发________小时后与小明相遇.
4.已知A地在C、B两地之间,甲乙两人分别从A、B两地同时出发,相向而行,经过一段时间后相遇,甲继续向B地前进,乙继续向A地前进;甲到达B地后立即返回,在C地甲追上乙.甲乙两人相距的路程y(米)与出发的时间x(分钟)之间的关系如图所示,则A、C两地相距________米.
5.甲、乙两人在1800米长的直线道路上跑步,甲、乙两人同起点、同方向出发,并分别以不同的速度匀速前进.已知,甲出发30秒后,乙出发,乙到终点后立即返回,并以原来的速度前进,最后与甲相遇,此时跑步结束.如图,y(米)表示甲、乙两人之间的距离,t(秒)表示甲出发的时间,图中折线及数据表示整个跑步过程中y与t函数关系.那么,乙到终点后________秒与甲相遇.
6.(2017 重庆)A、B两地之间的路程为2380米,甲、乙两人分别从A、B两地出发,相向而行,已知甲先出发5分钟后,乙才出发,他们两人在A、B之间的C地相遇,相遇后,甲立即返回A地,乙继续向A地前行.甲到达A地时停止行走,乙到达A地时也停止行走,在整个行走过程中,甲、乙两人均保持各自的速度匀速行走,甲、乙两人相距的路程y(米)与甲出发的时间x(分钟)之间的关系如图所示,则乙到达A地时,甲与A地相距的路程是________米.
7.(2017 随州)在一条笔直的公路上有A、B、C三地,C地位于A、B两地之间,甲车从A地沿这条公路匀速驶向C地,乙车从B地沿这条公路匀速驶向A地,在甲车出发至甲车到达C地的过程中,甲、乙两车各自与C地的距离y(km)与甲车行驶时间t(h)之间的函数关系如图所示.下列结论:①甲车出发2h时,两车相遇;②乙车出发1.5h时,两车相距170km;③乙车出发2 h时,两车相遇;④甲车到达C地时,两车相距40km.其中正确的是________(填写所有正确结论的序号).
8.甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地. 如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系式;折线B C D表示轿车离甲地距离y(千米)与x(小时)之间的函数关系.
下几种说法:
①货车的速度为60千米/小时;
②轿车与货车相遇时,货车恰好从甲地出发了3. 9小时;
③若轿车到达乙地后,马上沿原路以CD段速度返回,则轿车从乙地出发 小时再次与货车相遇;
其中正确的个数是________. (填写序号)
9.在一条笔直的高速公路上依次有3个标志点A、B、C,甲、乙两车分别从A、C两点同时出发,匀速行驶,甲车从A→B→C,乙车从C→B→A,甲、乙两车离B的距离y1、y2(千米)与行驶时间x(小时)之间的函数关系图象如图所示.观察图象,给出下列结论:①A、C之间的路程为690千米;②乙车比甲车每小时快30千米;③4.5小时两车相遇;④点E的横坐标表示两车第二次相遇的时间;⑤点E的坐标为(7,180)其中正确的有________(把所有正确结论的序号都填在横线上).
10.小明在上学的路上(假定从家到校只有这一条路)发现忘带眼镜,立刻停下,往家里打电话,妈妈接到电话后立刻带上眼镜赶往学校.同时,小明原路返回,两人相遇后小明立即赶往学校,妈妈回家,妈妈要15分钟到家,小明再经过3分钟到校.小明始终以100米/分的速度步行,小明和妈妈之间的距离y(米)与小明打完电话后的步行时间t(分)之间函数图象如图所示,则下列结论:①打电话时,小明与妈妈的距离为1250米;②打完电话后,经过23分钟小明到达学校;③小明与妈妈相遇后,妈妈回家的速度为150米/分;④小明家与学校的距离为2550米.其中正确的有________ (把正确的序号都填上)
11.不览夜景,未到重庆.山城夜景,早在清乾隆时期就已有名气,被时任巴县知县王尔鉴,列为巴渝十二景之一.在朝天门码头坐船游两江(即长江、嘉陵江),是游重庆赏夜景的一个经典项目.一艘轮船从朝天门码头出发匀速行驶,1小时后一艘快艇也从朝天门码头出发沿同一线路匀速行驶,当快艇先到达目的地后立刻按原速返回并在途中与轮船第二次相遇.设轮船行驶的时间为t(h),快艇和轮船之间的距离为y(km),y与t的函数关系式如图所示.问快艇与轮船第二次相遇时到朝天门码头的距离为________千米.
12.甲、乙两辆汽车分别从A、B两地同时出发,沿同一条公路相向而行,乙车出发2h后休息,与甲车相遇后,继续行驶.设甲、乙两车与B地的距离分别为y甲(km)、y乙(km),甲车行驶的时间为x(h),y甲、y乙与x之间的函数图像如图所示,现有4种说法:①甲车的速度是80km/h;②乙车休息了1小时;③两车相距80km时,甲车行驶了3小时;④乙车两次行驶的速度相同.上述说法正确的有________个.
13.已知甲、乙两车分别从A、B两地同时出发,以各自的速度匀速相向而行,两车相遇后,乙车继续向终点A地行使,而甲车原地停留了一段时间后才继续驶向终点B地,两车到达各自的终点后分别停止运动.若整个过程中,甲、乙两车各自的速度均保持不变,且甲、乙两车之间的距离s(千米)与乙车行驶时间t(小时)的函数图象如图所示,则甲车比乙车早到________小时.
二、综合题(共8题;共84分)
14.如图,王爷爷家院子里有一块三角形田地ABC,AB=AC=5米,BC=6米,现打算把它开垦出一个矩形MNFE区域种植韭菜,△AMN区域种植芹菜,△CME和△BNF区域种植青菜(开垦土地面积损耗均忽略不计),其中点M,N分别在AC,AB上,点E,F在BC上,已知韭菜每平方米收益100元,芹菜每平方米收益60元,青菜每平方米收益40元,设CM=5x米,王爷爷的蔬菜总收益为W元.
(1)当矩形MNFE恰好为正方形时,求韭菜种植区域矩形MNFE的面积.
(2)若种植韭菜的收益等于另两种蔬菜收益之和的2倍,求这时x的值.
(3)求王爷爷的蔬菜总收益为W关于x的函数表达式及W的最大值.
15.某商场销售一种成本为每件30元的商品,销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似看作一次函数y=-10x+600,商场销售该商品每月获得利润为w(元).
(1)求w与x之间的函数关系式;
(2)如果商场销售该商品每月想要获得2000元的利润,那么每月成本至少多少元?
(3)为了保护环境,政府部门要求用更加环保的新产品替代该商品,商场销售新产品,每月的销量与销售价格之间的关系与原产品的销售情况相同,新产品的成本每件32元,若新产品每月的销售量不低于200件时,政府部门给予每件4元的补贴,试求定价多少元时,每月销售新产品的利润最大?求出最大的利润。
16.为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.李明按照相关政策投资销售本市生产的一种新型节能灯.已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=-10x+500 .
(1)李明在开始创业的第一个月将销售单价定为20元,那么政府这个月为他承担的总差价为多少元
(2)设李明获得的利润为W(元),当销售单价定为多少元时,每月可获得最大利润
(3)物价部门规定,这种节能灯的销售单价不得高于25元.如果李明想要每月获得的利润不低于3000元,那么政府为他承担的总差价最少为多少元
17.为了解都匀市交通拥堵情况,经统计分析,都匀彩虹桥上的车流速度v(千米/小时)是车流密度x(辆/千米)的函数,当桥上的车流密度达到220辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度为20辆/千米时,车流速度为80千米/小时.研究表明:当20≤x≤220时,车流速度v是车流密度x的一次函数.
(1)求彩虹桥上车流密度为100辆/千米时的车流速度;
(2)在交通高峰时段,为使彩虹桥上车流速度大于40千米/小时且小于60千米/小时,应控制彩虹桥上的车流密度在什么范围内?
(3)当车流量(辆/小时)是单位时间内通过桥上某观测点的车辆数,即:车流量=车流速度×车流密度.当20≤x≤220时,求彩虹桥上车流量y的最大值.
18.为节约用水,某市居民生活用水按阶梯式水价计量,水价分为三个阶梯,价格表如下表所示:
某市自来水销售价格表
类别 月用水量 (立方米) 供水价格 (元/立方米) 污水处理费 (元/立方米)
居民生活用水 阶梯一 0~18(含18) 1.90 1.00
阶梯二 18~25(含25) 2.85
阶梯三 25以上 5.70
(注:居民生活用水水价=供水价格+污水处理费)
(1)当居民月用水量在18立方米及以下时,水价是________元/立方米.
(2)4月份小明家用水量为20立方米,应付水费为:
18×(1.90+1.00)+2×(2.85+1.00)=59.90(元)
预计6月份小明家的用水量将达到30立方米,请计算小明家6月份的水费.
(3)为了节省开支,小明家决定每月用水的费用不超过家庭收入的1%,已知小明家的平均月收入为7530元,请你为小明家每月用水量提出建议
19.为响应荆州市“创建全国文明城市”号召,某单位不断美化环境,拟在一块矩形空地上修建绿色植物园,其中一边靠墙,可利用的墙长不超过18m,另外三边由36m长的栅栏围成.设矩形ABCD空地中,垂直于墙的边AB=xm,面积为ym2(如图).
甲 乙 丙
单价(元/棵) 14 16 28
合理用地(m2/棵) 0.4 1 0.4
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)若矩形空地的面积为160m2 , 求x的值;
(3)若该单位用8600元购买了甲、乙、丙三种绿色植物共400棵(每种植物的单价和每棵栽种的合理用地面积如下表).问丙种植物最多可以购买多少棵?此时,这批植物可以全部栽种到这块空地上吗?请说明理由.
20.某公司计划从甲、乙两种产品中选择一种生产并销售,每年产销 x 件,已知产销两种产品的有关信息 如下:
产品 每件售价/万元 每件成本/万元 年最大产销量/件
甲 6 3 200
乙 20 10 80
甲、乙两产品每年的其他费用与产销量的关系分别是: y1 = kx + b 和 y2 =ax2+ m ,它们的函数图象分别如图(1)和图(2)所示.
(1)求: y1 、 y2 的函数解析式;
(2)分别求出产销两种产品的最大利润;(利润=销售额-成本-其它费用)
(3)若通过技术改进,甲产品的每件成本降到 a 万元,乙产品的年最大产销量可以达到 110 件,其它都不变,为获得最大利润,该公式应该选择产销哪种产品?请说明理由.
21.嘉兴某公司抓住“一带一路”的机遇不断创新发展,生产销售某产品.该产品销售量y(万件)与售价x(元/件)之间存在图1(一条线段)所示的变化趋势,总成本P(万元)与销售量y(万件)之间存在图2所示的变化趋势,当6≤y≤10时可看成一条线段,当10≤y≤18时可看成抛物线P=- y2+8y+m.
(1)写出y与x之间的函数关系式;
(2)若销售量不超过10万件时,利润为45万元,求此时的售价为多少元/件
(3)当售价为多少元时,利润最大,最大值是多少万元 (利润=销售总额-总成本)
答案解析部分
一、填空题
1.【答案】320
【解析】【解答】由图象可知甲的速度为:80÷1=80(米/分),
乙的速度为:80-(140-80)÷(4-1)=60(米/分),
由于乙后出发,出发3分钟后返回A地,甲、乙两人同时达到B地和A地,所以甲从A地到B地共用时4+3=7(分),
A、B两地相距80×7=560米,
560÷(80+60)=4,
所以甲、乙两人最后相遇时,乙距B地的路程是560-60×4=320(米),
故答案为:320.
【分析】根据图像求出甲乙的速度,再求出甲从A地到B地共用的时间,及A、B两地的路程,然后求出甲、乙两人最后相遇时,乙距B地的路程即可。
2.【答案】60
【解析】【解答】解:快车的速度为560÷7=80(km/h), 慢车的速度为560÷4﹣80=60(km/h),
快车到达甲地时,慢车距离甲地的距离为(80﹣60)×(7﹣4)=60(km).
故答案为:60.
【分析】根据速度=路程÷时间,即可求出快车的速度,由慢车速度=两地间的距离÷两车相遇时间﹣快车速度,即可求出慢车的速度,再根据路程=两车速度之差×行驶时间即可得出结论.
3.【答案】0.7
【解析】【解答】解:爸爸的速度为36÷(1﹣0.1)=40(千米/小时),
小明的速度为36÷(1.2+0.3)=24(千米/小时).
设爸爸出发t小时后与小明相遇,此时,小明出发了(t+0.3)小时,
根据题意得:40(t﹣0.1)=24(t+0.3),
解得:t=0.7.
答:爸爸出发0.7小时后与小明相遇.
故答案为:0.7.
【分析】由图像可求出二人速度,根据相遇时二人距离家的路程相等列出方程40(t﹣0.1)=24(t+0.3),可求出时间.
4.【答案】 450
【解析】【解答】解:甲乙两人的速度和为450÷3=150(米/分钟),
甲的速度为450÷5=90(米/分钟),
乙的速度为150﹣90=60(米/分钟),
设A、C两地相距m米,则B、C两地相距(m+450)米,
根据题意得: ,
解得:m=450,
故答案为:450.
【分析】根据题意可以求出甲和乙的速度之和,甲和乙二人各自的速度。根据二人在过程中所用的时间相同,即可列出等量关系式,求出m的值。
5.【答案】
【解析】【解答】解:甲的速度为90÷30=3(米/秒), 乙的速度为3+90÷(120﹣30)=4(米/秒).
乙到达终点时,甲出发的时间为1800÷4+30=480(秒),
此时甲离终点的距离为1800﹣3×480=360(米),
乙返回后与甲相遇的时间为360÷(3+4)= (秒).
故答案为: .
【分析】根据速度=路程÷时间可求出甲的速度,由乙的速度=甲的速度+二者速度差可求出乙的速度,利用时间=路程÷速度可求出乙到达终点的时间,结合路程=速度×时间可求出此时甲离终点的距离,再根据相遇所需时间=甲离终点的距离÷甲、乙速度和,即可得出结论.
6.【答案】180
【解析】【解答】解:由题意可得, 甲的速度为:(2380﹣2080)÷5=60米/分,
乙的速度为:(2080﹣910)÷(14﹣5)﹣60=70米/分,
则乙从B到A地用的时间为:2380÷70=34分钟,
他们相遇的时间为:2080÷(60+70)=16分钟,
∴甲从开始到停止用的时间为:(16+5)×2=42分钟,
∴乙到达A地时,甲与A地相距的路程是:60×(42﹣34﹣5)=60×3=180米,
故答案为:180.
【分析】根据题意和函数图象中的数据可以求得甲乙的速度和各段用的时间,从而可以求得乙到达A地时,甲与A地相距的路程.
7.【答案】②③④
【解析】【解答】解:①观察函数图象可知,当t=2时,两函数图象相交, ∵C地位于A、B两地之间,
∴交点代表了两车离C地的距离相等,并不是两车相遇,结论①错误;
②甲车的速度为240÷4=60(km/h),
乙车的速度为200÷(3.5﹣1)=80(km/h),
∵(240+200﹣60﹣170)÷(60+80)=1.5(h),
∴乙车出发1.5h时,两车相距170km,结论②正确;
③∵(240+200﹣60)÷(60+80)=2 (h),
∴乙车出发2 h时,两车相遇,结论③正确;
④∵80×(4﹣3.5)=40(km),
∴甲车到达C地时,两车相距40km,结论④正确.
综上所述,正确的结论有:②③④.
故答案为:②③④.
【分析】①观察函数图象可知,当t=2时,两函数图象相交,结合交点代表的意义,即可得出结论①错误;②根据速度=路程÷时间分别求出甲、乙两车的速度,再根据时间=路程÷速度和可求出乙车出发1.5h时,两车相距170km,结论②正确;③根据时间=路程÷速度和可求出乙车出发2 h时,两车相遇,结论③正确;④结合函数图象可知当甲到C地时,乙车离开C地0.5小时,根据路程=速度×时间,即可得出结论④正确.综上即可得出结论.
8.【答案】 ①②③
【解析】【解答】由图象可知:货车是匀速行驶,速度=300÷5=60千米/小时,故①正确;
设线段DC的解析式是y=kx+b,
根据题意得:
解得: ,
则线段DC的解析式是:y=110x-195(2.5≤x≤4.5)
设OA的解析式是:y=mx,
根据题意得:5m=300,
解得:m=60,
则函数解析式是:y=60x,
根据题意得:
解得: ,
则轿车与货车相遇时,货车恰好从甲地出发了3.9小时,故②正确;
设轿车从乙地出发x小时再次与货车相遇,
∵V货车=60千米/时,CD段V轿车= (千米/时),
∴110x+60(x+4.5)=300,
解得x= (小时),故③正确.
故答案是:①②③.
【分析】 ①根据图象提供的信息解决问题,横轴代表的是货车从甲地去乙地的行驶时间,纵轴代表的是货车离甲的距离,由A点(5,300)可知甲乙两地相距300千米,货车行驶了5小时,根据速度等于路程除以时间即可算出货车的速度,②只要找出线段OA与CD交点的横坐标即可判断出②是否正确,利用待定系数法求出线段CD,OA的解析式,再解两解析式组成的方程组,即可求出其交点坐标,进而得出结论;③首先根据路程除以时间等于速度,算出轿车行驶CD段的速度, 若轿车到达乙地后,马上沿原路以CD段速度返回, 则轿车与货车实际是一个相遇问题,设轿车从乙地出发x小时再次与货车相遇,根据货车所走的路程+轿车所走的路程等于甲乙两地的全程即可列出方程,求解即可判断③的正确与否。
9.【答案】①②⑤
【解析】【解答】①450+240=690(千米).
故A、C之间的路程为690千米是正确的;
②450÷5-240÷4
=90-60
=30(千米/小时).
故乙车比甲车每小时快30千米是正确的;
③690÷(450÷5+240÷4)
=690÷(90+60)
=690÷150
=4.6(小时).
故4.6小时两车相遇,原来的说法是错误的;
⑤(450-240)÷(450÷5-240÷4)
=210÷(90-60)
=210÷30
=7(小时),
450÷5×7-450
=630-450
=180(千米).
故点E的坐标为(7,180)是正确的,
故其中正确的有①②⑤.
故答案为:①②⑤.
【分析】①抓住已知条件:甲、乙两车分别从A、C两点同时出发,由450+240计算即可求解; ②根据速度=路程÷时间求出两车的速度,再相减即可求解; ③根据相遇时间=路程和÷速度和路程算式计算即可求解; ④根据时间=路程差÷速度差求解即可.
10.【答案】①②④
【解析】【解答】解:①当t=0时,y=1250,
∴打电话时,小明与妈妈的距离为1250米,①正确;
②∵23﹣0=23(分钟),
∴打完电话后,经过23分钟小明到达学校,②正确;
③妈妈来学校的速度为:1250÷5﹣100=150(米/分),
二者相遇时,离家的距离为:150×5=750(米),
妈妈回家的速度为:750÷15=50(米/分),
∴③不正确;
④小明家与学校的距离为750+(23﹣5)×100=2550(米),
∴④正确.
综上可知:其中正确的结论有①②④.
故答案为:①②④.
【分析】①根据函数图象可知,当t=0时,y=1250,从而得出①正确;②结合函数图象可得知,小明打完电话后23分钟到校,从而得出②正确;③根据“妈妈来学校的速度=二者间的距离÷时间﹣小明的速度”代入数据即可得出妈妈赶往学校的速度,再依据“妈妈离家的距离=妈妈赶往学校的速度×时间”即可得出二者相遇时,妈妈离家的距离,最后由“妈妈回家的速度=离家的距离÷时间”即可得出结论,从而得出③不正确;④根据“小明家离学校的距离=二者相遇时离家的距离+小明的速度×相遇后小明赶到学校的时间”代入数据即可得知④成立.综上即可得出结论.
11.【答案】55
【解析】【解答】解:如图,轮船2小时后在A处,1.5小时后在B处相遇, 小时后快艇到达目的地C,设再过x小时在D处相遇,设轮船是速度为akm/h,快艇的速度为bkm/h.
由题意0.5(b﹣a)=a,解得b=3a,
由题意( ﹣ )(3a﹣a)= ,
解得a=20,
由题意x(3a+a)= ,
∴x= ,
( + )×20=55,
∴快艇与轮船第二次相遇时到朝天门码头的距离55km.
故答案为55.
【分析】如图,轮船2小时后在A处,1.5小时后在B处相遇, 小时后快艇到达目的地C,设再过x小时在D处相遇,设轮船是速度为akm/h,快艇的速度为bkm/h.列出方程求出a的值,再求出x的值,即可解决问题.
12.【答案】1
【解析】【解答】解:由图像可得, 甲车的速度为:400÷5=80km/h,故①正确,
甲车与乙车相遇时,甲车行驶的时间为:(400﹣200)÷80=2.5h,
∴乙车休息的时间为2.5﹣2=0.5h,故②错误,
由图像可知,两车相距80km,存在两种情况,故③错误,
乙车休息前行驶的速度为:200÷2=100km/h,乙车休息后行驶的速度为:(400﹣200)÷(5﹣2.5)=80km/h,
∵100≠80,故④错误,
故答案为:1.
【分析】根据题意和函数图像可以判断题目中的各个小题是否正确,从而可以解答本题.
13.【答案】
【解析】【解答】解:由题意乙的速度= =60千米/小时,
甲的速度= =80千米/小时,
甲从A到B需要 = 小时,
中途休息了 = 小时,
∴甲时间行驶时间= + = 小时,
7﹣ = ,
∴甲车比乙车早到 小时.
故答案为: .
【分析】根据图像,根据图像提供的信息,先求出甲乙的速度,再分别求出甲从A到B的时间及中途休息的时间,甲行驶的时间,然后求出甲车比乙车早到的时间。
二、综合题
14.【答案】 (1)解:作AH⊥BC于H,交MN于D.
∵AB=AC,AH⊥BC,
∴CH=HB=3,
在Rt△ACH中,AH= =4,
∵ME∥AH,
∴ = = ,
∴CE=3x,EM=EF=4x,
易证△MEC≌△NFB,
∴CE=BF=3x,
∴3x+4x+3x=6,
∴x= ,
∴EM= ,
∴矩形MNFE的面积为 平方米
(2)解:由题意:100×4x (6﹣6x)=2 [60× ×(6﹣6x) (4﹣4x)+40×4x×3x],
解得x= 或
(3)解:由题意W=100×4x (6﹣6x)+60× ×(6﹣6x) (4﹣4x)+40×4x×3x=﹣1200x2+960x+720=﹣1200(x﹣ )2+912,
, ∵﹣1200<0,
∴x= 时,W有最大值,最大值为912元.
【解析】【分析】(1)作AH⊥BC于H,交MN于D,利用勾股定理求出AH的长,再根据平行得线段成比例,设 CE=3x,EM=EF=4x, 结合已知条件易证△MEC≌△NFB,就可得出CE=BF=3x,然后根据BC=6,列方程求解即可。
(2)此题的等量关系是: 种植韭菜的收益=另两种蔬菜收益之和×2,设未知数,列方程求解即可。
(3)根据题意列出W与x的函数解析式,再将函数解析式转化为顶点式,利用二次函数的性质,就可求出W的最大值。
15.【答案】(1)解:w=(x﹣30)(﹣10x+600)=﹣10x2+900x﹣18000
(2)解:由题意得,﹣10x2+900x﹣18000=2000,解得:x1=40,x2=50,当x=40时,成本为30×(﹣10×40+600)=6000(元),当x=50时,成本为30×(﹣10×50+600)=3000(元),∴每月想要获得2000元的利润,每月成本至少3000元
(3)解:当y<200时,即:﹣10x+600<200,解得:x>40,w=(x﹣32)(﹣10x+600)=﹣10(x﹣46)2+1960,∵a=﹣10<0,x>40,∴当x=46时,w最大值=1960(元);
当y≥200时,即:﹣10x+600≥200,解得:x≤40,w=(x﹣32+4)(﹣10x+600)=﹣10(x﹣44)2+2560,∵a=﹣10<0,∴抛物线开口向下,当32<x≤40时,w随x的增大而增大,∴当x=40时,w最大值=2400(元),∵1960<2400,∴当x=40时,w最大.
答:定价每件40元时,每月销售新产品的利润最大,最大利润为2400元.
【解析】【分析】(1)利用利润法则:单件利润销量=利润,可列出函数表达式;(2)根据函数关系式的特殊值,列出方程,解方程求出结果;(3)根据销量进行分类讨论,分别列出分段函数,在自变量的取值范围内,根据二次函数的单调性,求出最值.
16.【答案】(1)解:在y=-10x+500中,x=20 y=300300(12-10)=600 承担总差价为600元
(2)解:W=(-10x+500)(x-10)=-10(x-30)2+4000x=30时,W有最大值4000
(3)解:W=-10(x-30) +4000 令W≥3000 画出草图, 由图像可知 有20≤x≤40 ∵x≤25 ∴20≤x≤25 在y=-10x+500中,-10<0 ∴y随x的增大而减小 ∴x=25时,y最小为250 ∴政府为他承担总差价最少为250(12-10)=500元
【解析】【分析】(1)将x=20代入y=-10x+500,求出y的值,利用成本价和出厂价,可列式计算求出结果。
(2)利用李明获得的利润为W=每一件的利润×销售量,列出W与x的函数解析式,将其函数解析式转化为顶点式,利用二次函数的性质求解。
(3)结合函数图形,根据已知条件, 就可求出销售单价不得高于25元 且每月获得的利润不低于3000元 时, 政府为他承担的总差价。
17.【答案】(1)解:设车流速度v与车流密度x的函数关系式为v=kx+b,由题意,得
,
解得: ,
∴当20≤x≤220时,v=﹣ x+88,
当x=100时,v=﹣ ×100+88=48(千米/小时)
(2)解:由题意,得
,
解得:70<x<120,
∴应控制大桥上的车流密度在70<x<120范围内
(3)解:设车流量y与x之间的关系式为y=vx,
当20≤x≤220时,
y=(﹣ x+88)x=﹣ (x﹣110)2+4840,
∴当x=110时,y最大=4840,
∵4840>1600,
∴当车流密度是110辆/千米,车流量y取得最大值是每小时4840辆
【解析】【分析】(1)用待定系数法求一次函数解析式。(2)利用不等式组求不等式组解集。(3)利用车流量=车流速度×车流密度关系式列出二次函数解析式配方为顶点式,求最值.
18.【答案】(1)1.90
(2)解:由题意可得:
小明家6月份的水费是:(1.9+1)×18+(2.85+1)×7+(5.70+1)×5=112.65(元)
(3)解:由题意可知,当用水量为18立方米时,应交水费52.2元,当用水量为25立方米时,应交水费79.15元,而小明家计划的水费不超过75.3元,由此可知他们家的用水量不超过18立方米,而不足25立方米,设他们家的用水量为x立方米,则由题意可得:
18×(1.9+1)+(x-18)×(2.85+1) 75.3,解得:x 24,
∴当小明家每月的用水量不要超过24立方米时,水费就不会超过他们家庭总收入的1%.
【解析】【解答】解:(1)由表中数据可知,当用水量在18立方米及以下时,水价为1.9元/立方米;
【分析】(1)由 某市自来水销售价格表中的信息可知, 当居民月用水量在18立方米及以下时,水价 为 1.90 元/立方米 ;
(2) 4月份小明家用水量为20立方米,属于表格中的第二阶梯,所以应付水费为两部分: 18立方米及以下时,水价 按(1.90+1)元/立方米计算,超过部分按( 2.85+1.00 )元/立方米计算,再把两部分相加即可求解;
6月份小明家的用水量将达到30立方米, 则按阶梯三计算:18立方米及以下时,水价 按(1.90+1)元/立方米计算,超过部分按( 2.85+1.00 )元/立方米计算,超过25以上的按( 5.70+1 )元/立方米计算,再把这三部分相加即可求解;
(3)由题意根据小明家的平均月收入为7530元 可计算出小明家计划的水费不超过75.3元, 列出不等式即可求解。
19.【答案】 (1)解:y=x(36﹣2x)=﹣2x2+36x(9≤x<18)
(2)解:由题意:﹣2x2+36x=160,
解得x=10或8.
∵x=8时,36﹣16=20>18,不符合题意,
∴x的值为10.
(3)解:∵y=﹣2x2+36x=﹣2(x﹣9)2+162,
∴x=9时,y有最大值162,
设购买了乙种绿色植物a棵,购买了丙种绿色植物b棵,
由题意:14(400﹣a﹣b)+16a+28b=8600,
∴a+7b=1500,
∴b的最大值为214,此时a=2,
需要种植的面积=0.4×(400﹣214﹣2)+1×2+0.4×214=161.2<162,
∴这批植物可以全部栽种到这块空地上.
【解析】【分析】(1)先用含x的代数式表示出BC的长为(36-2x),然后根据矩形的面积公式计算即可。最后根据各边长大于0和BC的长不超过墙长列出不等式组,解之求出x的取值范围。
(2)当y=160时得 -2x2+36x=160, 解方程求得x的值,注意检验x的值是否符合题意(在取值范围内)。
(3)先根据二次函数的性质求出面积的最大值;又设购买了乙种绿色植物a棵,购买了丙种绿色植物b棵,根据购买总费列出方程,从而求得b的最大整数值为214,此时a=2,然后求出此时的种植面积,由此时的种植面积小于空地的最大面积判断出这批植物可以全部栽种到这块空地上.
20.【答案】 (1)解:依题意得: ,所以 ,所以, ;
由已知可得: ,所以, ,所以, .
(2)解: , ( ),
2>0, ,
∴x=200时, .
,( ).
, 时,
∴x=80时,
(3)解: , ,
, ,
∴x=200时, ,
, ,
∴x=100时, ,
① ,解得 ,
当 时,选择两种产品一样.
② 解得 ,
当 时,选择甲产品.
③ ,解得
当 时,选择乙产品.
, (1) , ;(2)x=200时, ,x=80时, ;
【解析】【分析】(1)观察函数图像可知:直线y1经过点(0,10),(200,210),直线y1经过点(0,40),(80,360),利用待定系数法,分别求出两函数解析式即可。
(2)根据总利润=(每一件的售价-每一件的成本价)×数量-y,分别列出函数解析式,根据自变量的取值范围及一次函数和二次函数的性质,就可求出产销两种产品的最大利润 。
(3)由题意可知,甲产品的售价为a元,根据甲的总利润W1=(每一件的售价-每一件的成本价)×数量-y1 , 再列出W2与x的函数关系式,利用二次函数的性质,可求出最大利润时x的值;再分情况讨论:W1=460;W1>460;W1<460;分别求出a的取值范围,即可解答此题。
21.【答案】 (1)解:设y=kx+b,把(6,18),(18,6)代入得
解得
∴y=-x+24
(2)解:当6≤y≤10时,可得14≤x≤18,
x(-x+24)-10y=45,
即-x2+34x-240=45
解得x=15或x=19(舍去)
∴此时售价为15元/件。
(3)解:把(10,100)代入P= y2+8y+m得到m=40
∴P= y2+8y+40
①当6≤x≤10时,10≤y≤18,
w=x(-x+24)-( y2+8y+40)= (x-14)2+40
∴当x=14时,w最大值为40万元
②当14≤x≤18时,6≤y≤10,
W=x(-x+24)-10y=-(x-17)2+49
∴当x=17时,w最大值为49万元。
∴综上所述,当x=17时w最大值为49万元。
【解析】【分析】(1)观察图像,将 点(6,18)和点(18,6)代入 y=kx+b ,就可求出y与x的函数解析式。
(2)根据当6≤y≤10时,可求出x的取值范围为14≤x≤18,再根据销售量不超过10万件时,利润为45万元,建立关于x的方程,解方程求出符合题意的x的值,即可求解。
(3)将点(10,100)代入 P= y2+8y+m,可求出m的值,即可得出p与y的函数解析式,再分情况讨论: ①当6≤x≤10时,10≤y≤18;②当14≤x≤18时,6≤y≤10,分别列出W与x的函数解析式,利用二次函数的性质解答即可。
21世纪教育网(www.21cnjy.com)
同课章节目录
