【专题训练】二次函数应用动态图形分类练习(含解析)
文档属性
| 名称 | 【专题训练】二次函数应用动态图形分类练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-10 06:09:47 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
二次函数应用动态图形分类练习
一、二次函数——周长线段之和最小
1.如图,在平面直角坐标系中,抛物线 经过 轴上的 点,直线 与抛物线在第一象限交于点 .
(1)求直线 的函数解析式;
(2)已知点 是抛物线的对称轴上的一个动点,当 的周长最小时,求 的面积;
(3)若以点 , , , 为顶点的四边形是平行四边形,则点 的坐标是________.
2.综合与探究
如图,在平面直角坐标系中,抛物线 与 轴分别交于点 和点 (点 在点 的左侧),交 轴于点 .点 是线段 上的一个动点,沿 以每秒1个单位长度的速度由点 向点 运动,过点 作 轴,交抛物线于点 ,交直线 于点 ,连接 .
(1)求直线 的表达式;
(2)在点 运动过程中,运动时间 为何值时, ?
(3)在点 运动过程中, 的周长是否存在最小值?若存在,求出此时点 的坐标;若不存在,请说明理由.
3.综合与探究
如图,抛物线 与 轴相交于 , 两点,与 轴相交于点 , , ,直线 是抛物线的对称轴,在直线 右侧的抛物线上有一动点 ,连接 , , , .
(1)求抛物线的函数表达式:
(2)若点 在 轴的下方,当 的面积是 时,求 的面积;
(3)在直线 上有一点 ,连接 , ,则 的最小值为________;
(4)在(2)的条件下,点 是 轴上一点,点 是抛物线上一动点,是否存在点 ,使得以点 , , , 为顶点的四边形是平行四边形,若存在,请直接写出点 的坐标;若不存在,请说明理由.
4.综合与探究
如图,在平面直角坐标系中,抛物线 与 轴交于点 、 两点(点 在点 左侧),与 轴交于点 . 、 的长是不等式组 的整数解 ,点 在抛物线上.
(1)求抛物线的解析式及 的值;
(2) 轴上的点 使 + 的值最小,则 ________;
(3)将抛物线向上平移,使点 落在点 处.当 时,抛物线向上平移了________个单位;
(4)点 在 轴上,平面直角坐标系内存在点 使以点 、 、 、 为顶点的四边形为菱形,请直接写出点 的坐标.
二、二次函数——线段最值、面积倍数、最值
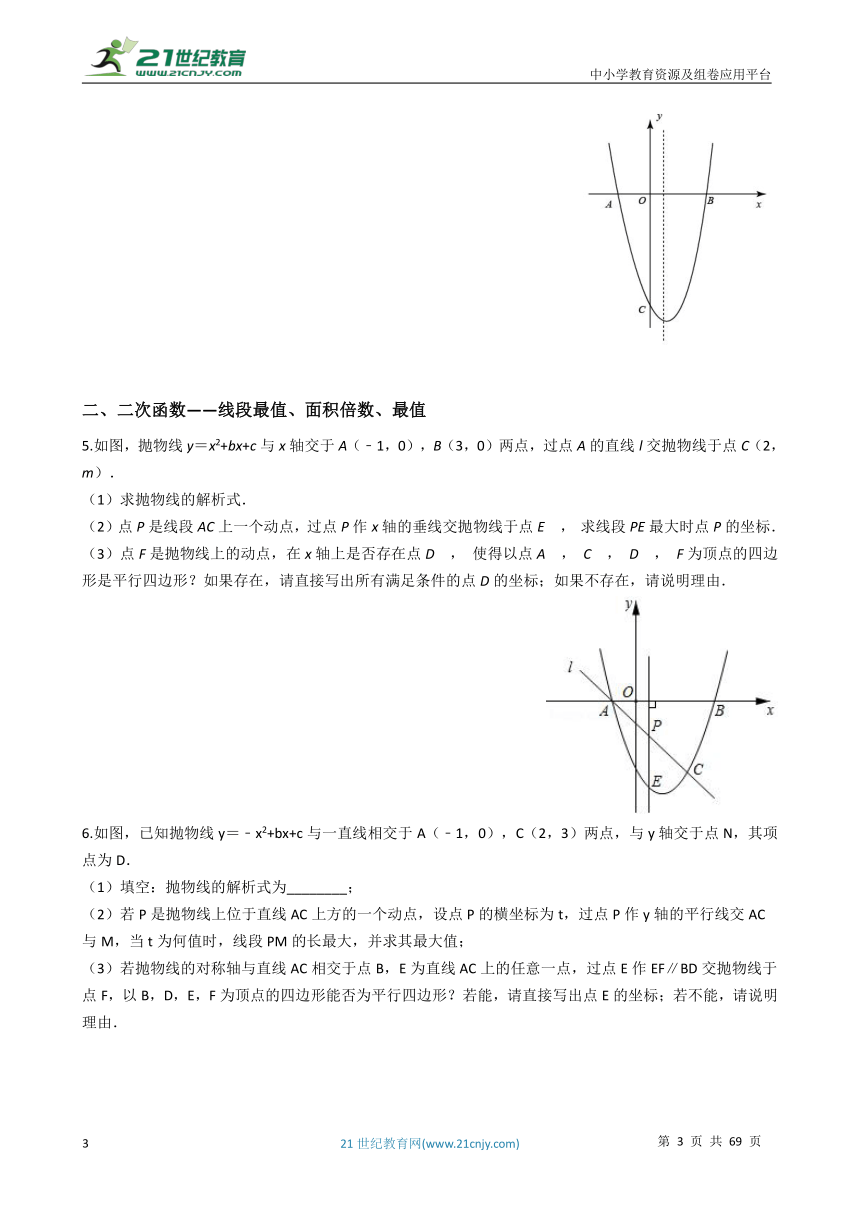
5.如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,过点A的直线l交抛物线于点C(2,m).
(1)求抛物线的解析式.
(2)点P是线段AC上一个动点,过点P作x轴的垂线交抛物线于点E , 求线段PE最大时点P的坐标.
(3)点F是抛物线上的动点,在x轴上是否存在点D , 使得以点A , C , D , F为顶点的四边形是平行四边形?如果存在,请直接写出所有满足条件的点D的坐标;如果不存在,请说明理由.
6.如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(﹣1,0),C(2,3)两点,与y轴交于点N,其项点为D.
(1)填空:抛物线的解析式为________;
(2)若P是抛物线上位于直线AC上方的一个动点,设点P的横坐标为t,过点P作y轴的平行线交AC与M,当t为何值时,线段PM的长最大,并求其最大值;
(3)若抛物线的对称轴与直线AC相交于点B,E为直线AC上的任意一点,过点E作EF∥BD交抛物线于点F,以B,D,E,F为顶点的四边形能否为平行四边形?若能,请直接写出点E的坐标;若不能,请说明理由.
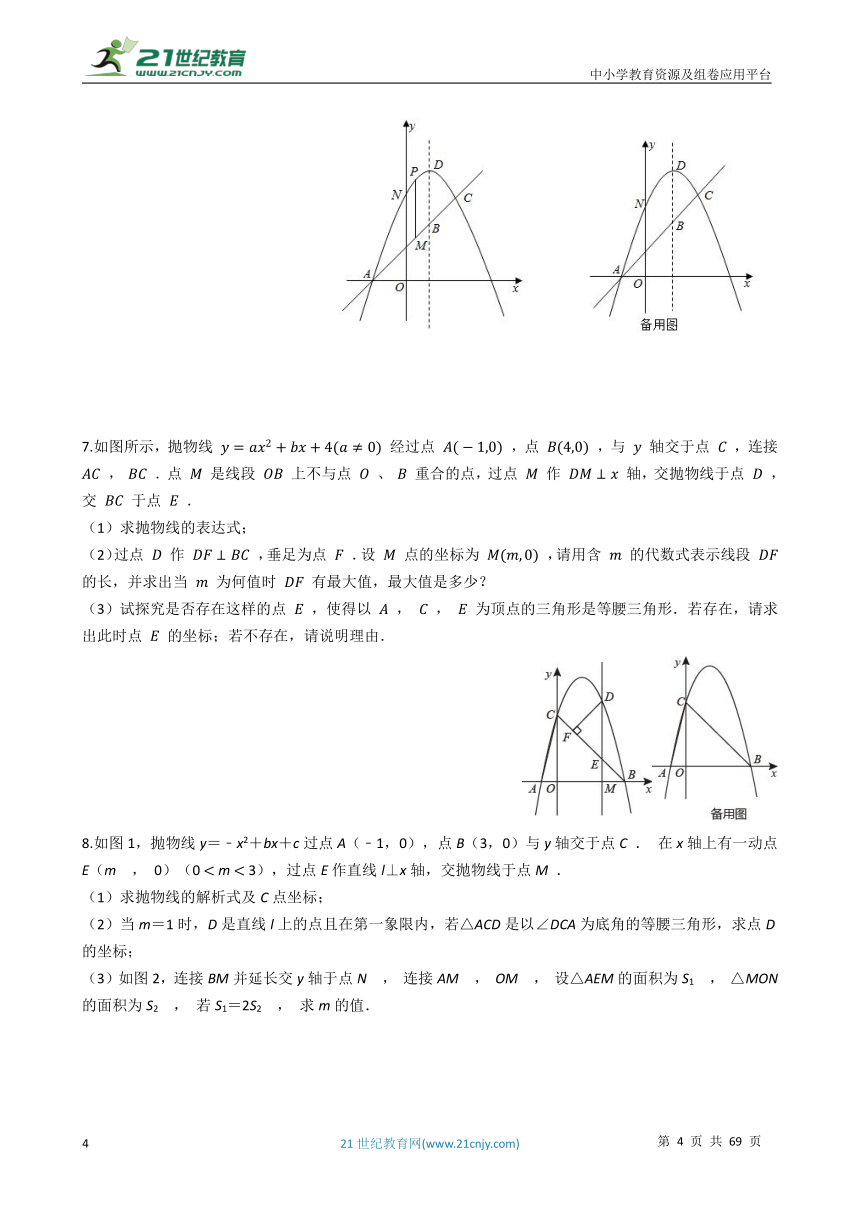
7.如图所示,抛物线 经过点 ,点 ,与 轴交于点 ,连接 , .点 是线段 上不与点 、 重合的点,过点 作 轴,交抛物线于点 ,交 于点 .
(1)求抛物线的表达式;
(2)过点 作 ,垂足为点 .设 点的坐标为 ,请用含 的代数式表示线段 的长,并求出当 为何值时 有最大值,最大值是多少?
(3)试探究是否存在这样的点 ,使得以 , , 为顶点的三角形是等腰三角形.若存在,请求出此时点 的坐标;若不存在,请说明理由.
8.如图1,抛物线y=﹣x2+bx+c过点A(﹣1,0),点B(3,0)与y轴交于点C . 在x轴上有一动点E(m , 0)(0 m 3),过点E作直线l⊥x轴,交抛物线于点M .
(1)求抛物线的解析式及C点坐标;
(2)当m=1时,D是直线l上的点且在第一象限内,若△ACD是以∠DCA为底角的等腰三角形,求点D的坐标;
(3)如图2,连接BM并延长交y轴于点N , 连接AM , OM , 设△AEM的面积为S1 , △MON的面积为S2 , 若S1=2S2 , 求m的值.
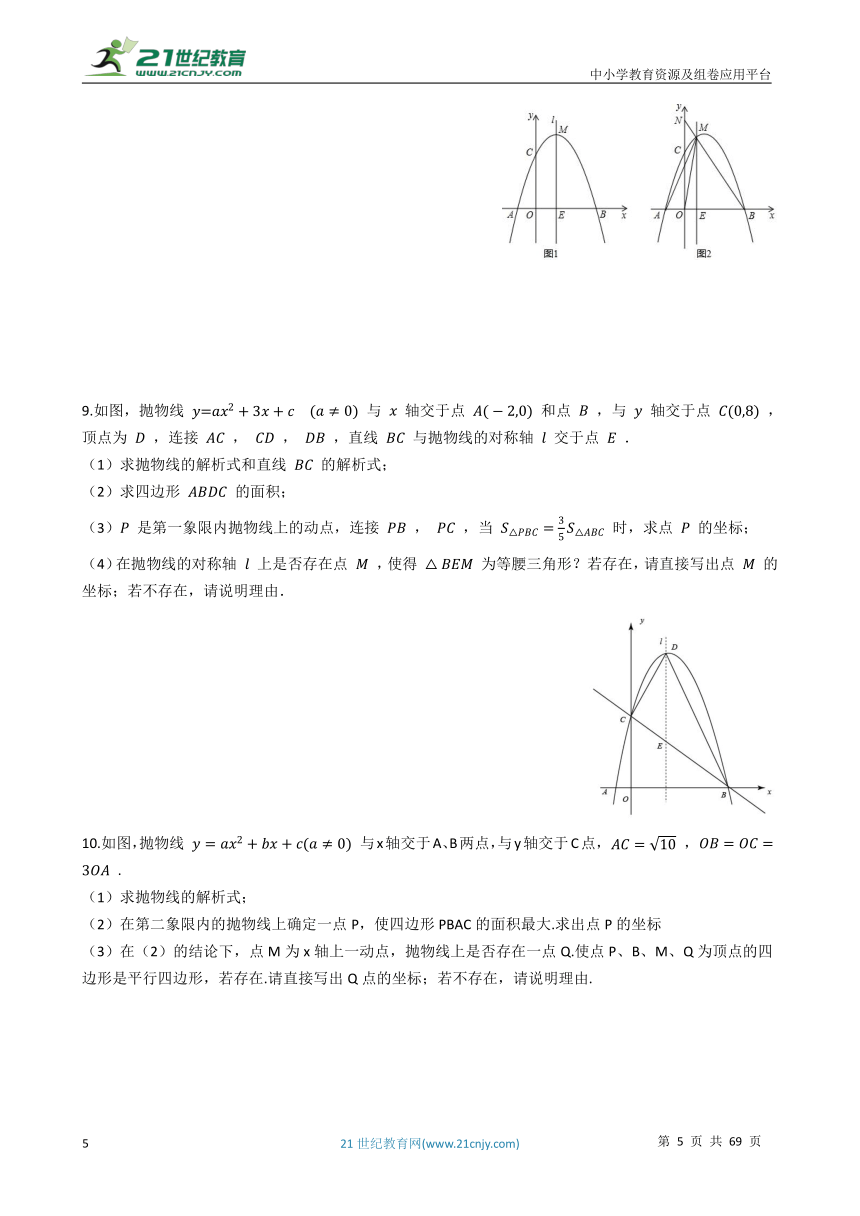
9.如图,抛物线 与 轴交于点 和点 ,与 轴交于点 ,顶点为 ,连接 , , ,直线 与抛物线的对称轴 交于点 .
(1)求抛物线的解析式和直线 的解析式;
(2)求四边形 的面积;
(3) 是第一象限内抛物线上的动点,连接 , ,当 时,求点 的坐标;
(4)在抛物线的对称轴 上是否存在点 ,使得 为等腰三角形?若存在,请直接写出点 的坐标;若不存在,请说明理由.
10.如图,抛物线 与x轴交于A、B两点,与y轴交于C点, , .
(1)求抛物线的解析式;
(2)在第二象限内的抛物线上确定一点P,使四边形PBAC的面积最大.求出点P的坐标
(3)在(2)的结论下,点M为x轴上一动点,抛物线上是否存在一点Q.使点P、B、M、Q为顶点的四边形是平行四边形,若存在.请直接写出Q点的坐标;若不存在,请说明理由.
11.如图1,在平面直角坐标系中,已知抛物线 与x轴交于 , 两点,与y轴交于点C .
(1)求抛物线的二次函数解析式:
(2)若点P在抛物线上,点Q在x轴上,当以点B、C、P、Q为顶点的四边形是平行四边形时,求点P的坐标;
(3)如图2,点H是直线 下方抛物线上的动点,连接 , ,当 的面积最大时,求点H的坐标.
三、二次函数——等腰三角形
12.如图,在平面直角坐标系中,已知点C(0,4),点A、B在x轴上,并且OA=OC=4OB , 动点P在过A、B、C三点的抛物线上.
(1)求抛物线的函数表达式;
(2)在直线AC上方的抛物线上,是否存在点P , 使得△PAC的面积最大?若存在,求出P点坐标及ΔPAC面积的最大值;若不存在,请说明理由.
(3)在x轴上是否存在点Q , 使得△ACQ是等腰三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
13.在平面直角坐标系中,直线 与x轴相交于点A , 与y轴相交于点C , 点B在x轴的负半轴上,且 ,抛物线经过点A , B , C , 点M为第一象限内抛物线上的一动点,过点M作直线 轴,交x轴于点 .
(1)求这条抛物线的函数表达式;
(2)如图1,当l经过抛物线顶点时,点D是抛物线对称轴上一点,若以C , B , D为顶点的三角形是等腰三角形,求点D坐标;
(3)如图2,连接 交y轴于点F , 连接 , ,若 的面积等于 的面积,求n的值.
14.如图,二次函数 的图象与 轴交于 , 与 轴交于点 .若点 , 同时从 点出发,都以每秒1个单位长度的速度分别沿 , 边运动,其中一点到达端点时,另一点也随之停止运动.
(1)求该二次函数的解析式及点 的坐标;
(2)当点 运动到 点时,点 停止运动,这时,在 轴上是否存在点 ,使得以 , , 为顶点的三角形为等腰三角形?若存在,请直接写出 点坐标;若不存在,请说明理由.
(3)当 , 运动到 秒时, 沿 翻折,点 恰好落在抛物线上 点处,请判定此时四边形 的形状,并求出 点坐标.
15.综合与探究
如图,在平面直角坐标系中,直线 与 轴交于点 ,与 轴交于点 .抛物线 经过 、 两点,且与 轴交于另一点 (点 在点 右侧).
(1)求抛物线的解析式及点 坐标;
(2)设该抛物线的顶点为点 ,则 ________;
(3)若点 是线段 上一动点,过点 的直线 平行 轴交 轴于点 ,交抛物线于点 .求 长的最大值及点 的坐标;
(4)在(3)的条件下:当 取得最大值时,在 轴上是否存在这样的点 ,使得以点 、点 、点 为顶点的三角形是等腰三角形?若存在,请直接写出所有点 的坐标;若不存在,请说明理由.
四、二次函数——直角三角形
16.如图,已知抛物线 ,与 轴交于点 和点 ,与 轴交于点 .
(1)求抛物线的解析式.
(2)坐标轴上是否存在点 ,使得 是直角三角形?若存在,求出点 的坐标:若不存在,说明理由.
17.如图10-1,以点 为顶点的抛物线与直线 交于 两点,且点A坐标为 ,点B在y轴上.
(1)求抛物线解析式;
(2)若点D是抛物线上位于直线 上方的一点(如图10-2),过点D作 轴于点E , 交直线 点F , 求线段 长度的最大值;
(3)在抛物线的对称轴 上是否存在点P , 使以点 为顶点的三角形是直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
18.如图,在平面直角坐标系中,已知抛物线 过A , B , C三点,点A的坐标是 ,点C的坐标是 ,动点P在抛物线上.
(1)求这个抛物线的解析式及顶点D的坐标;
(2)是否存在点P , 使得 是以 为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;
(3)设动点P的横坐标为m , 的面积为S.请直接写出面积S随着m的增大而减小时m的取值范围.
五、二次函数——等腰直角三角形(正方形)
19.如图,二次函数 的图象过点 ,交y轴于点C(0,-4).直线BO与抛物线相交于另一点D , 连接AB , AD , 点E是线段AB上的一动点,过点E作EF∥BD交AD于点F .
(1)求二次函数 的表达式;
(2)判断△ABD的形状,并说明理由;
(3)在点E的运动过程中,直线BD上存在一点G , 使得四边形AFGE为矩形,请判断此时AG与BD的数量关系,并求出点E的坐标;
(4)点H是抛物线的顶点,在(3)的条件下,点P是平面内使得∠EPF=90°的点在抛物线的对称轴上,是否存在点Q , 使得△HPQ是以∠PQH为直角的等腰直角三角形,若存在,直接写出符合条件的所有点Q的坐标;若不存在,请说明理由.
六、二次函数——平行四边形
20.如图,抛物线 的图象经过 三点,直线 经过点 ,交抛物线于点 .
(1)求抛物线的解析式;
(2)点 在线段 上,且满足 ,点 在 轴下方的抛物线上,设点 的横坐标为 ,当 为何值时, 的面积最大?并求出最大值;
(3) 为抛物线上的一动点, 为对称轴上一动点,若以 为顶点的四边形为平行四边形,求出点 的坐标.
21.如图,抛物线y= x2+bx+c与x轴交于点A和点B , 与y轴交于点C(0,﹣4),顶点为D , 其对称轴直线x=1交x轴于点P .
(1)求抛物线的解析式;
(2)如图1,线段MN的两端点M , N都在抛物线上(点M在对称轴左侧,点N在对称轴右侧),且MN=4,求四边形PMDN面积的最大值和此时点N的坐标;
(3)如图2,点Q是直线l:y=kx+1上一点,当以Q , A , C , B为顶点的四边形是平行四边形时,确定点Q的坐标和k的值.
22.如图,在平面直角坐标系中,抛物线 与x轴交于点 , ,与y轴交于点C.
(1)求该抛物线的解析式;
(2)直线l为该抛物线的对称轴,点D与点C关于直线l对称,点P为直线AD下方抛物线上一动点,连接PA,PD,求 面积的最大值;
(3)在(2)的条件下,将抛物线 沿射线AD平移 个单位,得到新的抛物线 ,点E为点P的对应点,点F为 的对称轴上任意一点,在 上确定一点G,使得以点D,E,F,G为顶点的四边形是平行四边形,写出所有符合条件的点G的坐标,并任选其中一个点的坐标,写出求解过程.
七、二次函数——矩形、菱形、正方形
23.如图,已知抛物线y=a +bx+3(a≠0)与x轴交于点A(1,0)和点B(-3,0),与y轴交于点C.
(1)求抛物线解析式;
(2)若M是抛物线对称轴上的一点,则△ACM周长的最小值为________;
(3)点N为第二象限抛物线上的动点,求△BCN面积的最大值及此时点N的坐标;
(4)点P是y轴上的一点,在坐标平面内存在点Q,使以A,C,P,Q为顶点的四边形是菱形,请直接写出点Q的坐标.
24.如图,抛物线 与x轴交于A , B两点(点A在点B左侧),与y轴交于点C .
(1)求A , B , C三点的坐标;
(2)连接 ,直线 与该抛物线交于点E , 与 交于点D , 连接 .当 时,求线段 的长;
(3)点M在y轴上,点N在直线 上,点P为抛物线对称轴上一点,是否存在点M , 使得以C、M、N、P为顶点的四边形是菱形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
25.综合与探究
如图,在平面直角坐标系中,抛物线 与x轴交于点A、B , 与y轴交于点C , 连接BC , ,对称轴为 ,点D为此抛物线的顶点.
(1)求抛物线的解析式;
(2)抛物线上C , D两点之间的距离是________;
(3)点E是第一象限内抛物线上的动点,连接BE和CE . 求 面积的最大值;
(4)点P在抛物线对称轴上,平面内存在点Q , 使以点B、C、P、Q为顶点的四边形为矩形,请直接写出点Q的坐标.
26.如图,抛物线 交x轴于 , 两点,交y轴于点C , 动点P在抛物线的对称轴上.
(1)求抛物线的解析式;
(2)当以P , B , C为顶点的三角形周长最小时,求点P的坐标及 的周长;
(3)若点Q是平面直角坐标系内的任意一点,是否存在点Q , 使得以A , C , P , Q为顶点的四边形是菱形?若存在,请直接写出所有符合条件的点Q的坐标;若不存在,请说明理由.
27.如图1,抛物线 与 轴交于 , 两点,与 轴交于点 .直线 经过抛物线上两点 , .已知点 , 的横坐标分别为 , 且满足 ,直线 的表达式为 .
(1)求 的值及抛物线的表达式;
(2)设点 是直线 上一动点,问:点 在什么位置上时, 的周长最小?求出点 的坐标及 周长的最小值;
(3)如图2, 是线段 上的一个动点,过点 作垂直于 轴的直线与直线 和抛物线分别交于点 , .若点 是直线 上一个动点,当点 恰好是线段 的中点时,在坐标平面内是否存在点 ,使以点 , , , 为顶点的四边形是菱形?若存在,请直接写出点 的坐标;若不存在,请说明理由.
答案解析部分
一、二次函数——周长线段之和最小
1.【答案】 (1)解:当y=0时, ,
解得x1=-4,x2=0,
点A(-4,0),
设直线 的函数解析式 ,过A、B两点,代入得
,
解方程组得 ,
直线 的函数解析式为 ;
(2)解:∵点 是抛物线的对称轴上的一个动点,抛物线对称轴为x= =-2,
∵C△BOQ的周长=OQ+QB+OB,点O,点B是定点,OB长是定值,
∴当 的周长最小时,就是OQ+QB最小,
∵点A与点O关于抛物线的对称轴对称,
∴点A,点Q,点B三点共线时,OQ+QB=AQ+QB≥AB最短,
当x =-2式, ,
点Q(-2,2),
S△BOQ的面积=S△BAO-S△QAO= ;
(3)(6,6)或(-2,6)或(-6,-6)
【解析】【解答】解:(3)以点A, , , 为顶点的四边形是平行四边形,分三种情况:
当以OB为对角线,四边形AONB为平行四边形,BN∥AO,且BN=AO,
设N1(x,y),
则y=6, x-4=2, x=6,
∴点N1(6,6);
当以AB为对角线,四边形AOBN为平行四边形是,NB∥AO,且NB=AO=4,
设N2(x,y),
则y=6, x+4=2, x=-2,
∴点N2(-2,6);
当以AO为对角线,四边形ANOB为平行四边形,AB∥ON,且AB=ON,
设N3(x,y),
∵6-0=0-y,2-0=-4-x,
∴y=-6, x=-6,
∴点N3(-6,-6);
∴以点A, , , 为顶点的四边形是平行四边形,则点 的坐标是(6,6)或(-2,6)或(-6,-6).
故答案为(6,6)或(-2,6)或(-6,-6).
【分析】(1)先求出 点A(-4,0), 再利用待定系数法求函数解析式即可;
(2)先求出 点A,点Q,点B三点共线时,OQ+QB=AQ+QB≥AB最短, 再求出 点Q(-2,2), 最后利用三角形的面积公式计算求解即可;
(3)分类讨论,结合图形,利用平行四边形的性质,列方程计算求解即可。
2.【答案】 (1)解:∵抛物线 与 轴分别交于点 和点 ,交 轴于点 ,
∴当 时, ,即 ,
当 时, , , ,即 , ,
设直线 的解析式为:
则 ,
∴ ,
∴直线 的表达式: .
(2)解:∵点 沿 以每秒1个单位长度的速度由点 向点 运动,
∴ , ,
∵ 轴,
∴ , ,
∴
∵ , ,
∴ , ,
∴△AOC是等腰直角三角形,
∴ ,由勾股定理得: ,
∵ 轴,
在 中, ,
∴△AEP也是等腰直角三角形,
∴ , ,
∴ ,
∴当 时,即 或 时, .
(3)解:在 中, ,
∴ ,
∴ 的周长: .
∴当 最小时 的周长最小.
当 时, 最小,
∵ ,
∴ ,
在 中, , , , ,
∴ ,
∴ ,
∴ .
【解析】【分析】(1)利用待定系数法进行求解即可;
(2)先求出 ,再求出 △AOC是等腰直角三角形, 最后进行求解即可;
(3)先求出 当 最小时 的周长最小 ,再求出 , 最后进行求解即可。
3.【答案】 (1)解:∵抛物线 与 轴相交于 , 两点, , ,
∴ ,
解得: ,
∴抛物线的解析式为:
(2)解:如图,过 作 轴于 ,交 于 ,
当 时, ,
∴ ,
设 的解析式为 ,则 ,
解得 ,
∴ 的解析式为: ,
设 ,则 ,
∴ ,
∵ 的面积是 ,
∴ ,
∴ ,
解得: 或3,
∵点 在直线 右侧的抛物线上,
∴ ,
∴ 的面积
(3)
(4)解:①当MB为对角线时,MN//BD,MN=BD,
过点N作NE⊥x轴于E,过当D作DF⊥x轴于F,
∵点D(3, ),
∴DF= ,
在△MNE和△BDF中, ,
∴△MNE≌△BDF,
∴DF=NE= ,
∵点D在x轴下方,MB为对角线,
∴点N在x轴上方,
∴点N纵坐标为 ,
把y= 代入抛物线解析式得: ,
解得: , ,
∴ ( , ), ( , )
如图,当BM为边时,MB//ND,MB=ND,
∵点D(3, ),
∴点N纵坐标为 ,
∴ ,
解得: , (与点D重合,舍去),
∴ ( , ),
综上所述:存在点 ,使得以点 , , , 为顶点的四边形是平行四边形,点 的坐标为: 或 或
【解析】【解答】(3)∵抛物线 与 轴相交于 , 两点,
∴点A与点B关于直线l对称,
∴BC为AP+CP的最小值,
∵B(4,0),C(0,-6),
∴AP+CP的最小值=BC= = .
故答案为:
【分析】(1)利用待定系数法求函数解析式即可;
(2)先求出 的解析式为: , 再求出 或3, 最后利用三角形的面积公式求解即可;
(3)先求出点A与点B关于直线l对称,再求出BC为AP+CP的最小值,最后利用勾股定理求解即可;
(4)分类讨论,利用全等三角形的性质与判定,再结合图象求解即可。
4.【答案】 (1)解:所给不等式组的解集为 , 其整数解为2,3.
∵OA,OB的长是所给不等式组的整数解,且OA∴ ,则A(-2,0),B(3,0)
∵点A、B在抛物线上,
∴ ,解得, .
∴所求的抛物线的解析式为
∵点D(2,m)在抛物线上,
∴
(2)2
(3)9
(4)解:∵以A、B、M、N为顶点的四边形是菱形,对角线互相垂直且平分,
由∵
∴AB与MN不能作为一组对角线.
∴分两种情况:
①以AM与BN为对角线时,如图2①和图2②.
如图2①,AB=OA+OB=2+3=5,
∵四边形ABMN是菱形,
∴MN∥AB∥x轴,MN=MB=AB=5.
在 中,
∴M(0,4).
∴N(-5,4).
如图2②,同理可得:N(-5,-4).
②以AN与BM为对角线时,如图2③和图2④.
如图2③,菱形的边长仍为5,MN∥x轴,
∵
∴
∴
如图2④,同理可得:
综合上述①、②两种情况,符合条件的点N的坐标为:
【解析】【解答】(2)如图1所示,连接AD交y轴于点E , 则此时AE+ED最小.
设直线AD的解析式为
∵点A(-2,0),D(2,-4)在直线 AD上,
∴ ,解得, .
∴直线AD的函数解析式为
当x=0时,y=-2,.即E(0, -2).
∴
故答案为:2
(3)如图1,
∵AD//FB ,
∴
∴
∵
∴
∵
∴
∴
∴抛物线向上平移9个单位.
故答案为:9
【分析】(1)利用待定系数法求出 抛物线的解析式为 再计算求解即可;
(2)先求出直线AD的函数解析式为 再求出E(0, -2),最后计算求解即可;
(3)先求出再求出最后求解即可;
(4)分类讨论,结合图形,利用勾股定理求解即可。
二、二次函数——线段最值、面积倍数、最值
5.【答案】 (1)解:将A(﹣1,0),B(3,0)代入y=x2+bx+c,
得到
解得 ,
∴y=x2﹣2x﹣3
(2)解:将C点的横坐标x=2代入y=x2﹣2x﹣3,得y=﹣3,∴C(2,﹣3);
∴直线AC的函数解析式是y=﹣x﹣1.
设P点的横坐标为x(﹣1≤x≤2),则P、E的坐标分别为:P(x,﹣x﹣1),E(x,x2﹣2x﹣3);
∵P点在E点的上方,PE=(﹣x﹣1)﹣(x2﹣2x﹣3)=﹣x2+x+2,
=﹣(x )2 ,
∵﹣1<0,
∴当x 时,PE的最大值 ,此时P( , )
(3)解:存在.
理由:如图,设抛物线与y的交点为K,由题意K(0,﹣3),
∵C(2,﹣3),
∴CK∥x轴,CK=2,
当AC是平行四边形ACF1D1的边时,可得D1(﹣3,0).
当AC是平行四边形AF1CD2的对角线时,AD2=CK,可得D2(1,0),
当点F在x轴的上方时,令y=3,3=x2﹣2x﹣3,
解得x=1± ,
∴F3(1 ,3),F4(1 ,3),
由平移的性质可知D3(4 ,0),D4(4 ,0).
综上所述,满足条件的点D的坐标为(﹣3,0)或(1,0)或(4 ,0)或(4 ,0).
【解析】【分析】
(1)将A、B两点坐标代入抛物线解析式,可以得到关于b和c的方程组,解方程组求出b和c,然后写出解析式即可;
(2)将点 点C(2,m) 代入解析式求出坐标,直线经过A、C两点,利用待定系数法求出直线解析式,设P点横坐标为x,利用直线AC解析式表示出纵坐标,E点横坐标也为x,纵坐标代入抛物线解析式表示出来,然后PE=两点纵坐标之差,整理出表达式,再求最值及点P的坐标即可;
(3)分情况讨论,四点中只有点A与点C是固定的,分别确定当AC为一边,当AC为对角线时,平行四边形的几种位置,然后计算的坐标。
6.【答案】 (1)y=﹣x2+2x+3
(2)解:设直线AC的解析式为y=mx+n,把A(﹣1,0),C(2,3)代入得,
,
解得, ,
直线AC的解析式为y=x+1,
依题意得,P(t,﹣t2+2t+3),M(t,t+1),
PM=﹣t2+2t+3-(t+1)= ﹣t2+t+2=-(t- )2+ ,
当t= 时,PM有最大值,最大值为
(3)解:∵y=﹣x2+2x+3=﹣(x﹣1)2+4
∴顶点D(1,4),把x=1代入y=x+1得,y=2,
∴B(1,2),BD=2,
设点E(m,m+1),则F(m,﹣m2+2m+3),EF= ,
∵EF∥BD,
∴当EF=BD时,以B,D,E,F为顶点的四边形能为平行四边形.
∴ =2,
当 时,
解得:m1=0,m2=1(舍去),
当 时,
解得m3= ,m4= ;
∴点E的坐标为:(0,1)或( , )或( , ).
【解析】【解答】解:(1)把A(﹣1,0),C(2,3)代入y=﹣x2+bx+c得,
,
解得, ,
抛物线的解析式为:y=﹣x2+2x+3;
故答案为:y=﹣x2+2x+3;
【分析】(1)先求出 , 再求函数解析式即可;
(2)利用待定系数法求出直线AC的解析式为y=x+1,再求解即可;
(3) 先求出 =2, 再分类讨论求解即可。
7.【答案】 (1)解:将点 、 的坐标代入抛物线表达式得 ,
解得 ,
∴抛物线的表达式为:
(2)解:由抛物线的表达式知,点 ,
设直线 的表达式为: ,
, ,
则 ,
解得: ,
直线 的表达式为: ;
设点 ,则点 ,点 ,
∴ ,
∵ ,故 ,
∴ ,
∴ ,
∵ ,
∴当 时, 有最大值为 ;
(3)解:存在,理由:
点 、 的坐标分别为 、 ,
则 ,过点 作 轴于点 ,
①当 时,
在 中, 由勾股定理得 ,
即 ,
解得: , (舍去),
故点 ;
②当 时,则 ,连接 .
在 中, 由勾股定理得 .
即 ,
解得: , (舍去),
则 ,
故点 ;
③当 时, ,
即 ,
解得: ;
则 ,
故点 ,
综上,点 的坐标为 或 或 .
【解析】【分析】(1)先求出a=-1,b=3,再求抛物线的解析式即可;
(2)利用待定系数法求出直线 的表达式为: ,再利用特殊角的锐角三角函数值计算求解即可;
(3)分类讨论,结合图象,利用勾股定理计算求解即可。
8.【答案】 (1)解:将点A、B的坐标代入抛物线表达式得 ,
解得 ,
故抛物线的表达式为y=﹣x2+2x+3,
当x=0时,y=3,故点C(0,3);
(2)解:当m=1时,点E(1,0),设点D的坐标为(1,a),
由点A、C、D的坐标得,AC= ,
同理可得:AD= ,CD= ,
①当CD=AD时,即 = ,解得a=1;
②当AC=AD时,同理可得a= (舍去负值);
故点D的坐标为(1,1)或(1, );
(3)解:∵E(m,0),则设点M(m,﹣m2+2m+3),
设直线BM的表达式为y=sx+t,则 ,
解得: ,
故直线BM的表达式为y=﹣ x+ ,
当x=0时,y= ,故点N(0, ),则ON= ;
S1= AE×yM= ×(m+1)×(﹣m2+2m+3),
2S2=ON xM= ×m=S1= ×(m+1)×(﹣m2+2m+3),
解得m=﹣2± (舍去负值),
经检验m= ﹣2是方程的根,
故m= ﹣2.
【解析】【分析】(1)将点A、B的坐标代入抛物线表达式得 , 解得即可得到抛物线的表达式;
(2)当m=1时,点E(1,0),设点D的坐标为(1,a), 由点A、C、D的坐标得,AC= ,同理可得:AD= ,CD= ,①当CD=AD时;②当AC=AD时,可得点D的坐标为(1,1)或(1, );
(3)S1= AE×yM,2S2=ON xM,即可求解。
9.【答案】 (1)解: 抛物线 过点 和 ,
解得
抛物线的解析式为 .
令 ,得 .
解得 , .
点 的坐标为 .
设直线 的解析式为 .
把点 , 分别代入 ,得
解得
直线 的解析式为
(2)解:如图,设抛物线的对称轴 与 轴交于点 .
抛物线的解析式为 ,
顶点 的坐标为 .
四边形 四边形
.
(3)解: .
.
如图,过点 作 轴,交 轴于点 ,交 于点 .
设点 .
点 在直线 上,
.
.
.
.
解得 , .
,
(4)解:存在.
直线 的解析式为
对称轴 为:
①当 时,点M与点H重合,
②当 时,
或者
③当 时, ,
点 的坐标为 或 或 或
【解析】【分析】(1)利用待定系数法求出抛物线的解析式为 ,再求出 点 的坐标为 ,最后求函数解析式即可;
(2)先求出顶点 的坐标为 ,再利用三角形的面积公式和四边形面积公式计算求解即可;
(3) 先求出 ,再求出 ,最后计算求解即可;
(4)先利用勾股定理求出BE的值,再分类讨论,求点的坐标即可。
10.【答案】 (1)解:∵OB=OC=3OA,AC= ,
∴ ,即 ,
解得:OA=1,OC=OB=3,
∴A(1,0),B(-3,0),C(0,3),代入 中,
则 ,解得: ,
∴抛物线的解析式为
(2)解:如图,四边形PBAC的面积=△BCA的面积+△PBC的面积,
而△ABC的面积是定值,故四边形PBAC的面积最大,只需要△BPC的最大面积即可,
过点P作y轴的平行线交BC于点H,
∵B(-3,0),C(0,3),设直线BC的表达式为y=mx+n,
则 ,解得: ,
∴直线BC的表达式为y=x+3,
设点P(x,-x2-2x+3),则点H(x,x+3),
S△BPC= = = ,
∵ ,故S有最大值,即四边形PBAC的面积有最大值,
此时x= ,代入 得 ,
∴P( , )
(3)解:若BP为平行四边形的对角线,
则PQ∥BM,PQ=BM,
则P、Q关于直线x=-1对称,
∴Q( , );
若BP为平行四边形的边,
如图,QP∥BM,QP=BM,
同上可得:Q( , );
如图,BQ∥PM,BQ=PM,
∵点Q的纵坐标为 ,代入 中,
解得: 或 (舍),
∴点Q的坐标为( , );
如图,BP∥QM,BP=QM,
∵点Q的纵坐标为 ,代入 中,
解得: (舍)或 ,
∴点Q的坐标为( , );
综上:点Q的坐标为( , )或( , )或( , )
【解析】【分析】(1)由已知易求得OA、OC=OB的值,于是可得点A、B、C的坐标,用待定系数法可求抛物线的解析式;
(2)由图知:S四边形PBAC=S△BCA+S△PBC , 而△ABC的面积是定值,所以要使四边形PBAC的面积最大,只需要△BPC的最大面积即可;结合二次函数的性质可求解;
(3)由题意可分三种情况讨论:
①若BP为平行四边形的对角线,则PQ∥BM,PQ=BM,则P、Q关于直线x=-1对称,于是可得点Q的坐标;
②若BP为平行四边形的边,则BQ∥PM,BQ=PM,同理可求解;
③若BP为平行四边形的边,则 BP∥QM,BP=QM,同理可求解.
11.【答案】 (1)解:∵点 , 在抛物线 上,
∴将 , 代入解析式,
得 ,
∴ ,
∴抛物线的二次函数解析为
(2)解:运用平行四边形对角线互相平分的性质和中点坐标公式求解,
设点 , ,
①当 为对角线时,则 ,即 ,
代入得 ,
解得 或 ,
∴得点 , ;
②当 为对角线时,则 ,
同理求得点 ,
③当 为对角线时,则
同理求得点 与点 重合,即 ;
综上所述, , ,
(3)解:如图,过点C作x轴的平行线,交 于点M;过点H作y轴的平行线,交 于点E,交 于点F,交x轴于点G.
设点H的坐标为 ,
∵ , ,
∴直线 的解析式为 ,
∴点F的坐标为 .
∵ , ,
∴直线 的解析式为 ,
∴点M的坐标为 .
求 的面积表达式有以下二种方法:
解法1:水平分割时,
.
当 时, 的面积最大,此时 ;
解法2:垂直分割时,
,
当 时,面积最大,此时 ,
解法3:如图下图,过点H作 的平行线l,
∵直线 的解析式为 ,直线l与直线平行,
∴直线l解析式的k=1,
∴设直线l的解析式为 ,
当直线l与抛物线相切时, 面积最大,
由 ,
消去y,得: ,①
当方程①的 时,直线l与抛物线相切,
, ,
∴ 为所求.
【解析】【分析】(1)把点 , 在抛物线 得抛物线为 ;
(2)①当 为对角线时,②当 为对角线时,③当 为对角线时,分三种情况讨论即可;
(3)设点H的坐标为 , , 由B、C的坐标得出直线 的解析式,由B、H的坐标得出直线 的解析式,即可得到点M的坐标,可利用水平分割、垂直分割两种方法都可求出 的面积表达式,由此得出当 的面积最大时,求出H的坐标。
三、二次函数——等腰三角形
12.【答案】 (1)解:∵C(0,4),∴OC=4.
∵OA=OC=4OB,∴OA=4,OB=1,
∴A(4,0),B( 1,0),
设抛物线解析式:y=a(x+1)(x 4),
∴4= 4a,∴a= 1.
∴y= x2+3x+4.
(2)解:存在.
作PN⊥x轴交AC于N,
AC的解析式为y=-x+4 ,
设P(x, x2+3x+4),则N(x,-x+4),
得PN=( x2+3x+4)-(-x+4)= x2+4x ,
∴S△PAC= PN×4=2PN=2( x2+4x)=-2(x-2)2+8 ,
当x=2时,ΔPAC面积的最大值为8,此时点P的坐标为(2,6).
∴P点坐标为(2,6)时,ΔPAC面积有最大值,最大面积是8 .
(3)Q(0,0),(-4,0),
【解析】【解答】解:(3) 设 根据勾股定理得:
①当 时,
此时可得Q的坐标为(4+4 ,0)、(4-4 ,0);
②当 时,
当 时,不合题意舍去,
③当 时,
综上,符合条件的点Q的坐标为:(0,0),(-4,0), .
【分析】(1)由C的坐标,得出OC的值,由OA=OC=4OB,得出OA=4,OB=1,以及A、B的坐标,设抛物线解析式:y=a(x+1)(x 4),解出a的值,即可得出抛物线的函数表达式;
(2)存在,作PN⊥x轴交AC于N,由A和C的坐标,得出AC的解析式,设P(x, x2+3x+4),则N(x,-x+4),得PN=( x2+3x+4)-(-x+4)= x2+4x ,得出S△PAC的值,当x=2时,ΔPAC面积的最大值为8,此时点P的坐标为(2,6).
(3)设 根据勾股定理得出 , ①当 时,②当 时,③当 时,三种情况分析即可得到点Q的坐标。
13.【答案】 (1)解:对于y=﹣x+3,令y=﹣x+3=0,解得x=3,令x=0,则y=3,
得,点A的坐标为(3,0),点C的坐标为(0,3),
∵AB=4,点B在x轴的负半轴上,
∴点B的坐标为(﹣1,0),
∵抛物线经过点A(3,0),C(﹣1,0),
∴设抛物线的解析式为y=a(x﹣3)(x+1),
将C(0,3)代入,得a=﹣1,
∴抛物线的解析式为y=﹣(x﹣3)(x+1),
即:y=﹣x2+2x+3;
(2)解:由题意得:BC= ,设D(1,m),
①当BD=CD时,BD2=CD2 ,
即:22+m2=12+(3﹣m)2 ,
解得:m=1,
∴D1(1,1);
②当BD=BC时,4+m2=10,解得 ,
∴ , ;
③当CD=BC时,1+(m﹣3)2=10,
解得:m1=6(舍去),m2=0,
∴D4(1,0);
综上所述,满足条件的D点的坐标是:D1(1,1), , ,D4(1,0);
(3)解:点M的坐标为(n,﹣n2+2n+3),
由题意得:tan∠MBN ,
∴OF 3﹣n,
∵S△MAN=S△MOF ,
∴ AN MN OF xM , 即 (3﹣n)(﹣n2+2n+3) (3﹣n)n,
即:﹣n2+2n+3=n,
解得: , (舍去),
∴n .
【解析】【分析】(1)由待定系数法即可求解;
(2)分BD=CD、BD=BC、CD=BC三种情况,分别求解即可;
(3)由S△MAN=S△MOF, 得到 AN MN OF xM, 即可求解。
14.【答案】 (1)解:∵二次函数 的图象与 轴交于 , ,
∴ , ,
∴ ,
∴该二次函数的解析式为 ,
当 时, ,
∴ ;
(2)解:如图1,存在满足条件的点 ,
∵ , ,
∴ ,
当点 运动到 点时,此时 ,
∴存在以下3种情况:
图1
①当 时,
∵ ,
∴ ,
∴ ,
∴点 坐标 ;
② ,此时 ,
∴ ,
∴ ,
∴点 坐标 ;
③当 时,
设此时 的坐标为 ,
则 ,
解得, 或 ,
∴ 或 ,
综上所述:点 坐标为 、 或 或 ;
(3)解:四边形 为菱形,
图2
如图2, 点关于 与 点对称,过点 作 于 ,
∵ , 沿 翻折,点 恰好落在抛物线上 点处,
∴ ,
∴平行四边形 为菱形,且 ,
∵ ,
∴ , ,
又∵ ,
∴ ∽ ,
∴ ,
∴ ,
∴ , ,
∴ ,
∵ ,
∴ ,
∵点 在二次函数 上,
代入解得 ,
∴ .
【解析】【分析】(1)根据韦达定理即可求得 、 的值,即可得到该二次函数的解析式,然后令 ,即可得到点 的纵坐标,此题得解;(2)由题目已知条件可知,存在满足条件的点 ,根据已知条件以及第(1)问可得 ,分以下三种情况分别讨论即可:① ;② ;③ ,即可得到点 的坐标;(3)如图2, 点关于 与 点对称,过点 作 于 ,根据题目已知条件以及翻折的意义可知四边形 为菱形;根据 可得 ∽ ,根据相似比即可求得 、 的值(用 表示),即可求得点 的坐标(用 表示),根据 ,即可求得点 的坐标(用 表示),再根据 在二次函数 上,即可求得 的值,进而可得点 的坐标.
15.【答案】 (1)∵直线y=-3x-3与x轴、y轴分别交于点A、C,
当 时,
∴
当 时,
∴
∵抛物线y=x2+bx+c经过点A、C,
∴
∴
∴抛物线的解析式是:
当 时,
解得:
∴
(2)3
(3)由(1)知 , 直线 的解析式是:
设 ,则
∴
当 时, 的最大值
∴点 的坐标为
(4)存在,如图,
由(2)得,当ME最大时,则D( ,0),M( , ),
∴DO=DB=DM= ;
∵∠BDM=90°,
∴OM=BM= .
点P1、P2、P3、P4在x轴上,
当点P1与原点O重合时,则P1M=BM= ,P1(0,0);
当BP2=BM= 时,则OP2= ,
∴P2( ,0);
当点P3与点D重合时,则P3M=P3B= ,
∴P3( ,0);
当BP4=BM= 时,则OP4= ,
∴P4 .
综上所述, .
【解析】【解答】设抛物线的对称轴交BC于点F , 交x轴于点G .
设直线BC的解析式为y=kx-3,则3k-3=0,解得k=1,
∴y=x-3;
∵y=x2-2x-3=(x-1)2-4,
∴抛物线的顶点H(1,-4),
当x=1时,y=1-3=-2,
∴F(1,-2),
∴FH=-2-(-4)=2,
∴ .
故答案为:3.
【分析】(1)直线y=-3x-3与x轴、y轴分别交于点A、C,当 时, , 当 时, , 得出A、C的坐标,因为抛物线y=x2+bx+c经过点A、C,得出b、c的值,即可得出抛物线的解析式,当 时, , 解得即可得出B的坐标;
(2)设抛物线的对称轴交BC于F点,求得直线BC的解析式,即可得出k=1,得到抛物线的顶点H,当x=1时,y=1-3=-2,即可求得 的面积;
(3)由(1)知 , 直线 的解析式是: , 设 , 则 , 当 时, 的最大值 , 即可得出点 的坐标;
(4)当点P1与原点O重合、当BP2=BM= 、当点P3与点D重合、当BP4=BM= 时,分情况讨论即可得出答案。
四、二次函数——直角三角形
16.【答案】 (1)解:根据题意得,
解得: ,
所以抛物线的解析式为:
(2)解:存在
分3种情况讨论:
①若 ,此时点 与原点 重合,所以
②若 ,过点 作 交 轴于点
∴ , ,
∴
∴
∴ ,即
∴ ,故
③若 ,过点 作 交 轴于点
∴ , ,
∴
∴
∴ ,即
∴ ,故
综上:存在点 , , 满足题意.
【解析】【分析】(1)将点A、B、C的坐标代入函数解析式,利用待定系数法求解即可;
(2)分情况讨论,结合函数图象,利用相似三角形的性质分别求解即可。
17.【答案】 (1)解:设抛物线的解析式为
顶点
把 代入解析式得:
抛物线的解析式 ;
(2)解:
设 ,则F的坐标为
当 时, 有最大值为2;
(3)解:存在,
①过点A作 于点
点 在对称轴直线 上
设 的坐标为
点A的坐标为
点 的坐标为
②过点A作 于点A,交直线 于点
于点A
于点
点 在对称轴直线 上
设 的坐标为
解此方程得:
点 的坐标为
综上所述,点P的坐标分别为 或 .
【解析】【分析】(1)设抛物线的解析式为 , 由顶点 , 得出 , 把 代入解析式得: , 由此得出a的值,即可得出抛物线解析式;
(2)由解析式得出 , 设 , 则F的坐标为 , 得出 , 当 时, 有最大值为2;
(3)存在,①过点A作 于点 , 由点 在对称轴直线 上,可设 的坐标为 , 因为 点A的坐标为 , 得出m的值,由此得出的坐标;②过点A作 于点A,交直线 于点 , 由 于点A,得出 , , 得出 , , 因为 , 点 在对称轴直线 上,得出设 的坐标为 , , , 解此方程得: , 得出点 的坐标为 。
18.【答案】 (1)解:将点A、C的坐标代入抛物线表达式得:
∴
∴此抛物线的解析式 .
∵ ,
∴顶点D的坐标为 ;
(2)解:存在;
①当 时:(如图1)
∵ ,
∴ .
∴ ,
∴ ,即
∴ , (舍)
∴ ;
②当 时:(如图2)
∵ ,
∴ ,
∴ ,即 .
∴ , (舍)
∴ .
∴符合条件的点P的坐标为 或 ;
(3) 或
【解析】【解答】解:(3)由图象可得 时, 的面积为S随着m的增大而减小;
∵顶点D的坐标为 ,点A的坐标是 ,
∴由图象可得 时,过点P作 轴交 于点N ,
设直线 的解析式 ,
∵点A的坐标是 ,点C的坐标是 ,
∴线 的解析式 ,
设点P的坐标是 ,则点 ,
∴ 的面积为 ,
当 时, 的面积有最大值,
∴ 时,S随着m的增大而减小.
∴面积S随着m的增大而减小时m的取值范围为 或 .
【分析】(1)先求出 再求出 此抛物线的解析式 ,最后求点的坐标即可;
(2)分类讨论,作图求解即可;
(3)先求出直线 的解析式 ,再利用三角形的面积公式进行计算求解即可。
五、二次函数——等腰直角三角形(正方形)
19.【答案】 (1)解:∵二次函数 的图象经过点A、点C,
∴ ,解得 .
∴二次函数的解析式为 .
(2)解:△ABD是直角三角形.理由如下:
∵点B(-2,m)在抛物线 上,
∴m= .
∴B(-2,-1).
∴直线OB的解析式为: ,
联立 ,解得: (即B点)或 ,
∴D(8,4),
∵A(4,-4),
∴由两点间距离公式得:
, , ,
∵ ,
∴△ABD是以BD为斜边的直角三角形;
(3)解:如图所示,
∵四边形AFGE为矩形,
∴EG∥AD,FG∥AB,
∵EF∥BD,
∴四边形EFDG和四边形FEBG都是平行四边形,
∴EF=GD,EF=BG,
∴BG=GD,
由(2)得△ABD为直角三角形,
∴AG= BD,
∵EG∥AD,
∴点E是AB的中点,
∴E ;
(4)存在,Q(2,﹣4)或(2, )
【解析】【解答】解:(4)如图,设EF的中点为K , P(x , y),连接PK ,
∵EF∥BD ,
∴ ,
又∵ ,
∴AF=FD , F为AD的中点,
由中点坐标公式可得,F(6,0),E ,
∵K为EF的中点,
∴K ,
根据两点间的距离公式可得: ,
∵∠EPF=90°,
∴点P在以K为圆心,EF为直径的圆上运动,
∵△PQH为等腰直角三角形,∠PQH=90°,
∴∠QHP=45°,
∴PQ∥x轴,
∴直线PH可看做由直线y=x平移得到,
则设直线PH的解析式为:y=x+b ,
∵抛物线的顶点为H(2,-5),
∴代入PH解析式得:b=-7,
∴直线PH的解析式为:y=x-7,
∵PK= EF ,
∴ ,
即: ,
解得: 或 ,
∵PQ∥x轴,
∴Q(2,﹣4)或(2, ).
【分析】(1)利用待定系数法计算求解即可;
(2)先求出直线OB的解析式为: , 再求出 , , , 最后求解即可;
(3)先求出四边形EFDG和四边形FEBG都是平行四边形,再求出点E是AB的中点,最后求点的坐标即可;
(4) 利用中点坐标公式,两点间的距离公式和勾股定理进行计算求解即可。
六、二次函数——平行四边形
20.【答案】 (1)解:∵抛物线 的图象经过点 ,
∴设抛物线的解析式为 .
把点 代入,
.
.
∴抛物线的解析式为 .
(2)解:∵直线 经过点 ,
.
∴直线 的解析式为 .
联立
解得 ,
∴点
.
设点 .
,
.
.
.
∴点 .
∴直线 的解析式为 .
如图,过点 作 轴交直线 于点 .
∵点 ,
.
设点B的横坐标为xB , 点E的坐标为xE ,
.
∴当 时,
有最大值为 .
(3)解:∵ ,
∴点Q的横坐标为2,
设点A,D,P,Q的横坐标分别为xA,xD,xP,xQ ,
若 为平行四边形的边,
∵以 为顶点的四边形为平行四边形,
.
或 .
或 .
∴点 的坐标为 或 ;
若 为平行四边形的对角线,
∵以 为顶点的四边形为平行四边形,
与 互相平分.
.
.
∵点 的坐标为 .
综上,当点 的坐标为 或 或 时,以 为顶点的四边形为平行四边形.
【解析】【分析】(1)将已知点的坐标代入二次函数的解析式,利用待定系数法确定二次函数的解析式即可;
(2)联立方程,解之即得出D的坐标,得出三角形ABD的面积,设点 . 因为 , 得到m的值,即得到直线 的解析式,过点 作 轴交直线 于点 . 设点B横坐标为xB, 点E的坐标为xE, 求出三角形FBE的面积,当 时, 有最大值;
(3)设点A,D,P,Q的横坐标分别为xA,xD,xP,xQ, 若 为平行四边形的边,得出 . 得出P的坐标,若 为平行四边形的对角线,得出 与 互相平分.分情况讨论即可。
21.【答案】 (1)解:由题意得: ,解得 ,
故抛物线的表达式为y= x2﹣x﹣4;
(2)解:由抛物线解析式得点D坐标为(1,﹣ ),
设四边形PMDN面积为S,
则S=S△PDM+S△PDN= PD(xN﹣xM)= (xN﹣xM),
故当MN与轴平行时,此时MN=4,S的面积最大,
则S=9,
此时点M、N关于抛物线对称轴对称,则点N的横坐标为3,
当x=3时,y= x2﹣x﹣4=﹣2.5,
故点N的坐标为(3,﹣2.5);
(3)解:把y=0代入y= x2﹣x﹣4得 x2﹣x﹣4=0,
解得: ,
∴点A(-2,0),点B(4,0)
设点Q的坐标为(m,km+1),
当AC为边时,如图1,
点A向右平移2个单位向下平移4个单位得到点C,同样点B向右平移2个单位向下平移4个单位得到点Q,
即 解得 ,
故点Q的坐标和k分别为(6,﹣4)、﹣ ;
如图2,
点A向右平移2个单位向下平移4个单位得到点C,同样点Q向右平移2个单位向下平移4个单位得到点B,
即 ,解得 ,
故点Q的坐标和k分别为(2,4)、1.5;
当AC是对角线时,
由中点公式得 解得 ,
故点Q的坐标和k分别为(﹣6,﹣4)、﹣ ;
综上,点Q的坐标和k分别为(6,﹣4)、﹣ 或(2,4)、1.5或(﹣6,﹣4)、﹣ .
【解析】【分析】(1)用待定系数法即可求解;
(2)由S=S△PDM+S△PDN= PD(xN﹣xM)= (xN﹣xM),即可求解;
(3)分AC为边、AC是对角线两种情况,利用图象平移和中点公式,分别求解即可.
22.【答案】 (1)解:将A(-1,0),B(4,0)代入y=ax2+bx-4得
,解得: ,
∴该抛物线的解析式为y=x2-3x-4,
(2)解:把x=0代入y=x2-3x-4中得:y=-4,
∴C(0,-4),
抛物线y=x2-3x-4的对称轴l为
∵点D与点C关于直线l对称,
∴D(3,-4),
∵A(-1,0),
设直线AD的解析式为y=kx+b;
∴ ,解得: ,
∴直线AD的函数关系式为:y=-x-1,
设P(m,m2-3m-4),
作PE∥y轴交直线AD于E,
∴E(m,-m-1),
∴PE=-m-1-(m2-3m-4)=-m2+2m+3,
∴ ,
∴ ,
∴当m=1时, 的面积最大,最大值为:8
(3)解:∵直线AD的函数关系式为:y=-x-1,
∴直线AD与x轴正方向夹角为45°,
∴抛物线沿射线AD方向平移平移 个单位,相当于将抛物线向右平移4个单位,再向下平移4个单位,
∵ , ,平移后的坐标分别为(3,-4),(8,-4),
设平移后的抛物线的解析式为
则 ,解得: ,
∴平移后y1=x2-11x+20,
∴抛物线y1的对称轴为: ,
∵P(1,-6),
∴E(5,-10),
∵以点D,E,F,G为顶点的四边形是平行四边形,分三种情况:
设G(n,n2-11n+20),F( ,y),
①当DE为对角线时,平行四边形的对角线互相平分
∴ ,∴
∴
②当EF为对角线时,平行四边形的对角线互相平分
∴ ,∴
∴
③当EG为对角线时,平行四边形的对角线互相平分
∴ ,∴
∴
∴ 或 或
【解析】【分析】(1)利用待定系数法,由点A,B的坐标求出函数解析式.
(2)由x=0求出对应的y的值,可得到点C的坐标,利用函数解析式求出抛物线的对称轴,利用轴对称的性质可求出点D的坐标;再利用待定系数法求出直线AD的解析式 , 设P(m,m2-3m-4), 作PE∥y轴交直线AD于E, 同时可表示出点E的坐标及PE的长,然后利用三角形的面积公式可得到△APD的面积与m之间的函数解析式,将其函数解析式转化为顶点式,利用二次函数的性质,可求出结果.
(3) 直线AD与x轴正方向夹角为45°,抛物线沿射线AD方向平移平移 个单位,相当于将抛物线向右平移4个单位,再向下平移4个单位,利用待定系数法求出平移后的函数解析式,同时可求出 抛物线y1的对称轴及点E的坐标;以点D,E,F,G为顶点的四边形是平行四边形,分三种情况:设G(n,n2-11n+20),F( ,y),①当DE为对角线时,平行四边形的对角线互相平分;②当EF为对角线时,平行四边形的对角线互相平分;③当EG为对角线时,平行四边形的对角线互相平分;分别利用线段的中点坐标建立关于n的方程,解方程求出n的值,即可得到点G的坐标.
七、二次函数——矩形、菱形、正方形
23.【答案】 (1)解:根据题意,得 ,
解方程组,得 ,
∴抛物线的解析式为y=﹣ ﹣2x+3
(2) +
(3)解:如图,过点N作直线NE⊥x轴,垂足为M,交直线BC于点E,
设直线BC的解析式为y=kx+n,
∵B(-3,0),C(0,3),
∴ ,
解方程组,得 ,
∴直线BC解析式为y=x+3,
设N(n,﹣ -2n+3),E(n,n+3),
∴NE=﹣ -2n+3-n-3=﹣ -3n,
∴ = + = +
= =﹣ - = ,
∴△BCN面积最大值 ,
此时,x= ,y= ,
故点
(4)解:如图,当AC为菱形的边时,
∵CP∥A ,AC= = ,
∴A = ,
∵A(1,0),
∴ (1, )或 (1,- );
当AC为菱形的对角线时,
设 (0,m),
∴A = ,C =3-m,
∴ ,
解得m= ,
∴C =3-m= ,
∴A = ,
∴ (1, );
当CP为菱形的对角线时,
作出点A关于CP的对称点即可,
∵A(1,0),
∴ (-1,0),
综上所述,点Q的坐标为(-1,0)或(1, )或(1, )或(1,- ).
【解析】【解答】(2)∵A , B是对称点,
∴抛物线的对称轴与BC的交点为△ACM周长最小位置,且最小值为BC+AC ,
∵A(1,0),B(-3,0),C(0,3),
∴AC= = ,BC= = ,
∴△ACM周长最小值为 + ,
故答案为: + ;
【分析】(1)利用待定系数法求函数解析式即可;
(2)先求出AC= = ,BC= = ,再计算求解即可;
(3)先求出直线BC解析式为y=x+3, 再求出 △BCN面积最大值 , 最后求点的坐标即可;
(4)分类讨论,利用勾股定理计算求解即可。
24.【答案】 (1)解:令x=0得 ,∴C点坐标(0,-8)
令y=0得:
解得:
∴A(-4,0),B(2,0)
(2)解:设DE交x轴于F,
设AC解析式为 ,代入AC坐标得:
,解得
∴AC解析式为
∵直线 与该抛物线交于点E,与 交于点D
∴
∴
∵
∴
∴
∴
∴
解得
∴
(3)解:抛物线 对称轴为
∵点M在y轴上,点N在直线 上,点P为抛物线对称轴上一点
∴设
当CM菱形的边时,则CM∥PN,CM=CN
∴N在对称轴上,即
∴
∴
解得
此时M点坐标为
当CM为菱形的对角线时,此时NP关于CM对称,即NP关于y轴对称
∴
∴
∵菱形对角线互相垂直平分
∴NP中点与CM中点是同一个点
∴
解得
此时M点坐标为
综上所述,存在M 、 使得以C、M、N、P为顶点的四边形是菱形.
【解析】【分析】(1)先求出 ,再求出 ,最后求点的坐标即可;
(2)先求出 AC解析式为 ,再求出 ,最后求解即可;
(3)先求出 ,再求出 ,最后求点的坐标即可。
25.【答案】 (1)解: 抛物线 的对称轴为 ,
,
,
,且点A在x轴负半轴上,
,
将点 代入 得: ,解得 ,
则抛物线的解析式为 ;
(2)
(3)解:如图,过点E作x轴的垂线,交 于点F,
,抛物线的对称轴为 ,
,
设直线 的解析式为 ,
将点 代入得: ,解得 ,
则直线 的解析式为 ,
设点E的坐标为 ,则 , ,
,
,
,
由二次函数的性质得:在 内,当 时, 取最大值,最大值为 ,
即 面积的最大值为 ;
(4) 或 或 或
【解析】【解答】解:(2) 化成顶点式为 ,
则顶点D的坐标为 ,
当 时, ,即 ,
则抛物线上 两点之间的距离是 ,
故答案为: ;
(4)设点P的坐标为 ,
由题意,分以下三种情况:
①当 为矩形 的边时,则 ,
设直线 的解析式为 ,
将点 代入得: ,
则直线 的解析式为 ,
将点 代入得: ,即 ,
将点C先向右平移2个单位长度,再向上平移4个单位长度可得到点P,
四边形 是矩形,
点C平移至点P的方式与点B平移至点Q的方式相同,
,
,即 ;
②当 为矩形 的边时,则 ,
同(4)①的方法可得:点Q的坐标为 ;
③当 为矩形 的对角线时,则 ,
,
即 ,
解得 或 ,
或 ,
当点P的坐标为 时,
则将点P先向左平移2个单位长度,再向下平移 个单位长度可得到点C,
四边形 是矩形,
点P平移至点C的方式与点B平移至点Q的方式相同,
,即 ;
同理可得:当点P的坐标为 时,点Q的坐标为 ,
综上,点Q的坐标为 或 或 或 .
【分析】(1)先求出点A的坐标,再求出 , 最后求函数解析式即可;
(2)先求出顶点D的坐标为 ,再求出 ,最后利用两点间的距离公式进行求解即可;
(3)利用待定系数法求出直线 的解析式为 , 再利用三角形的面积公式计算求解即可;
(4)分类讨论,利用矩形的性质、勾股定理、平移和点的坐标进行求解即可。
26.【答案】 (1)解:将 , 代入二次函数表达式中,
∴ ,解得 ,
∴二次函数的表达式为: ;
(2)解:连接BP、CP、AP,如下图所示:
由二次函数对称性可知,BP=AP,
∴BP+CP=AP+CP,
BC为定直线,当C、P、A三点共线时, 有最小值为 ,
此时 的周长也最小,
设直线AC的解析式为: ,代入 ,
∴ ,解得 ,
∴直线AC的解析式为: ,
二次函数的对称轴为 ,代入 ,得到 ,
∴P点坐标为(1,2),
此时 的周长最小值= ;
(3)解:Q点坐标存在,为(2,2)或(4, )或(4, )或( , )或( , )
【解析】【答案】解:(3) 设P点坐标为(1,t),Q点坐标为(m , n),
分类讨论:
情况一:AC为菱形对角线时,另一对角线为PQ ,
此时由菱形对角互相平分知:AC的中点也必定是PQ的中点,
由菱形对角线互相垂直知: ,
∴ ,解得 ,
∴P点坐标为(1,1),对应的Q点坐标为(2,2);
情况二:AP为菱形对角线时,另一对角线为CQ ,
同理有: ,解得 或 ,
∴P点坐标为(1, )或(1, ),对应的Q点坐标为(4, )或(4, );
情况三:AQ为菱形对角线时,另一对角线为CP ,
设P点坐标为(1,t),Q点坐标为(m , n),
同理有: ,解得 或 ,
∴P点坐标为(1, )或(1, ),对应的Q点坐标为(-2, )或(-2, );
纵上所示,Q点坐标存在,为(2,2)或(4, )或(4, )或( , )或( , ).
【分析】(1)将 , 代入二次函数表达式中,得出a、b的值,即可得到抛物线的解析式;
(2)连接BP、CP、AP,由二次函数对称性可知,BP=AP,得出 ,BC为定直线,当C、P、A三点共线时, 有最小值为 , 此时 的周长也最小,设直线AC的解析式为: , 代入 , 可得k、m的值,即可得到直线AC的解析式,二次函数的对称轴为 , 代入 , 得到 , 得到P的坐标,此时得到 的周长最小值;
(3)过点M作直线m//AC,直线m与抛物线交点即为P点,根据M的坐标可求出m的直线的表达式,联立抛物线的解析式与直线m的解析式即可求出p的坐标。
27.【答案】 (1)解:当 时,抛物线 ,
∴ (0,4),
∵点 在直线 上: 上,
∴ ,
∵直线 与 轴交点为 , ,
解得: ,
∴ (4,0),
∵点 在抛物线上,
∴ ①,
∵ ,
∴ 轴,点 、 关于抛物线对称轴对称,
∵ ,
∴抛物线对称轴为:直线 ,
∴ ②,
联立方程①②,
,
解得: ,
∴抛物线的表达式为 .
(2)解:连接 ,如图1,
∵ (0,4),点 是直线 上一动点,
∴ 、 关于直线 对称,∴ ,
∴当点 、 、 在同一直线上时, 最短,
当 时,解得: ,
∴此时, (2,2),
∵ ,
∴ ,
∴ 周长最小值为: .
(3)解:存在满足条件的点 ,
设 ( ),则 , ,
∵点 是 中点,
∴ ,
∴﹣ ,
解得: , (舍去),
∴ , , ,
①若 为菱形 边,点 在点 左侧,如图2,
延长 交 轴于点 ,
∵ , , ,
∴ °, ,
∴ ,
∴ , ,
∴ ,
②若 为菱形 边,点 在点 右侧,如图3,
∵ , , ,
∴ °, ,
∴ ,
∴ , ,
∴ ,
③若 为菱形的对角线,菱形 中,如图4,
设 与 交于点 ,
∴ , , ,
∴ 轴, ,
∴ ,
∴ ,
∴ ,
∴ .
当 、 为邻边时,
∵PM⊥MF,且PM=MF=FG=PG=3
∴四边形PMFG为正方形,
∵OM=1,
∴OF=OM+MF=1+3=4
可得 .
综上所述,满足条件的点 坐标为 或 或 或 .
【解析】【分析】(1)由抛物线过点C可求出C的坐标,由直线也经过点C即可求出n的值;得到n的值即有直线BC的关系式,即能求BC与x轴交点B的坐标,又由DE//x轴且其横坐标满足 , 即得到抛物线对称轴 , 再把点B坐标代入抛物线关系式得方程组,解得a、b的值即可;
(2)由于点Q在直线y=2上运动,要求的是OQ+BQ的最小值,O、B是定点,故寻找O或B关于直线y=2的对称点,由C(0,4)得C与O关于直线y=2对称,则有CQ=OQ,当点C、Q、B在同一直线上时有最小值,求直线BC上y=2时横坐标,即为Q的坐标,计算BC与OB的和即为三角形QOB周长最小值;
(3)先根据题意设点M、P、N坐标,利用P为MN中点的等量关系求出P、M的坐标,再对菱形四个顶点位置讨论:以PM为菱形的变,此时又分两种情况,分别是点F在点P左右侧的讨论;当F在P左侧时,根据菱形性质和GM与x轴夹角为45度易求G的坐标;当F在P右侧时,根据对称性即可求出G的坐标,以PM为菱形对角线,利用对角线互相垂直平分的性质即可求出点G坐标。
21世纪教育网(www.21cnjy.com)
二次函数应用动态图形分类练习
一、二次函数——周长线段之和最小
1.如图,在平面直角坐标系中,抛物线 经过 轴上的 点,直线 与抛物线在第一象限交于点 .
(1)求直线 的函数解析式;
(2)已知点 是抛物线的对称轴上的一个动点,当 的周长最小时,求 的面积;
(3)若以点 , , , 为顶点的四边形是平行四边形,则点 的坐标是________.
2.综合与探究
如图,在平面直角坐标系中,抛物线 与 轴分别交于点 和点 (点 在点 的左侧),交 轴于点 .点 是线段 上的一个动点,沿 以每秒1个单位长度的速度由点 向点 运动,过点 作 轴,交抛物线于点 ,交直线 于点 ,连接 .
(1)求直线 的表达式;
(2)在点 运动过程中,运动时间 为何值时, ?
(3)在点 运动过程中, 的周长是否存在最小值?若存在,求出此时点 的坐标;若不存在,请说明理由.
3.综合与探究
如图,抛物线 与 轴相交于 , 两点,与 轴相交于点 , , ,直线 是抛物线的对称轴,在直线 右侧的抛物线上有一动点 ,连接 , , , .
(1)求抛物线的函数表达式:
(2)若点 在 轴的下方,当 的面积是 时,求 的面积;
(3)在直线 上有一点 ,连接 , ,则 的最小值为________;
(4)在(2)的条件下,点 是 轴上一点,点 是抛物线上一动点,是否存在点 ,使得以点 , , , 为顶点的四边形是平行四边形,若存在,请直接写出点 的坐标;若不存在,请说明理由.
4.综合与探究
如图,在平面直角坐标系中,抛物线 与 轴交于点 、 两点(点 在点 左侧),与 轴交于点 . 、 的长是不等式组 的整数解 ,点 在抛物线上.
(1)求抛物线的解析式及 的值;
(2) 轴上的点 使 + 的值最小,则 ________;
(3)将抛物线向上平移,使点 落在点 处.当 时,抛物线向上平移了________个单位;
(4)点 在 轴上,平面直角坐标系内存在点 使以点 、 、 、 为顶点的四边形为菱形,请直接写出点 的坐标.
二、二次函数——线段最值、面积倍数、最值
5.如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,过点A的直线l交抛物线于点C(2,m).
(1)求抛物线的解析式.
(2)点P是线段AC上一个动点,过点P作x轴的垂线交抛物线于点E , 求线段PE最大时点P的坐标.
(3)点F是抛物线上的动点,在x轴上是否存在点D , 使得以点A , C , D , F为顶点的四边形是平行四边形?如果存在,请直接写出所有满足条件的点D的坐标;如果不存在,请说明理由.
6.如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(﹣1,0),C(2,3)两点,与y轴交于点N,其项点为D.
(1)填空:抛物线的解析式为________;
(2)若P是抛物线上位于直线AC上方的一个动点,设点P的横坐标为t,过点P作y轴的平行线交AC与M,当t为何值时,线段PM的长最大,并求其最大值;
(3)若抛物线的对称轴与直线AC相交于点B,E为直线AC上的任意一点,过点E作EF∥BD交抛物线于点F,以B,D,E,F为顶点的四边形能否为平行四边形?若能,请直接写出点E的坐标;若不能,请说明理由.
7.如图所示,抛物线 经过点 ,点 ,与 轴交于点 ,连接 , .点 是线段 上不与点 、 重合的点,过点 作 轴,交抛物线于点 ,交 于点 .
(1)求抛物线的表达式;
(2)过点 作 ,垂足为点 .设 点的坐标为 ,请用含 的代数式表示线段 的长,并求出当 为何值时 有最大值,最大值是多少?
(3)试探究是否存在这样的点 ,使得以 , , 为顶点的三角形是等腰三角形.若存在,请求出此时点 的坐标;若不存在,请说明理由.
8.如图1,抛物线y=﹣x2+bx+c过点A(﹣1,0),点B(3,0)与y轴交于点C . 在x轴上有一动点E(m , 0)(0 m 3),过点E作直线l⊥x轴,交抛物线于点M .
(1)求抛物线的解析式及C点坐标;
(2)当m=1时,D是直线l上的点且在第一象限内,若△ACD是以∠DCA为底角的等腰三角形,求点D的坐标;
(3)如图2,连接BM并延长交y轴于点N , 连接AM , OM , 设△AEM的面积为S1 , △MON的面积为S2 , 若S1=2S2 , 求m的值.
9.如图,抛物线 与 轴交于点 和点 ,与 轴交于点 ,顶点为 ,连接 , , ,直线 与抛物线的对称轴 交于点 .
(1)求抛物线的解析式和直线 的解析式;
(2)求四边形 的面积;
(3) 是第一象限内抛物线上的动点,连接 , ,当 时,求点 的坐标;
(4)在抛物线的对称轴 上是否存在点 ,使得 为等腰三角形?若存在,请直接写出点 的坐标;若不存在,请说明理由.
10.如图,抛物线 与x轴交于A、B两点,与y轴交于C点, , .
(1)求抛物线的解析式;
(2)在第二象限内的抛物线上确定一点P,使四边形PBAC的面积最大.求出点P的坐标
(3)在(2)的结论下,点M为x轴上一动点,抛物线上是否存在一点Q.使点P、B、M、Q为顶点的四边形是平行四边形,若存在.请直接写出Q点的坐标;若不存在,请说明理由.
11.如图1,在平面直角坐标系中,已知抛物线 与x轴交于 , 两点,与y轴交于点C .
(1)求抛物线的二次函数解析式:
(2)若点P在抛物线上,点Q在x轴上,当以点B、C、P、Q为顶点的四边形是平行四边形时,求点P的坐标;
(3)如图2,点H是直线 下方抛物线上的动点,连接 , ,当 的面积最大时,求点H的坐标.
三、二次函数——等腰三角形
12.如图,在平面直角坐标系中,已知点C(0,4),点A、B在x轴上,并且OA=OC=4OB , 动点P在过A、B、C三点的抛物线上.
(1)求抛物线的函数表达式;
(2)在直线AC上方的抛物线上,是否存在点P , 使得△PAC的面积最大?若存在,求出P点坐标及ΔPAC面积的最大值;若不存在,请说明理由.
(3)在x轴上是否存在点Q , 使得△ACQ是等腰三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
13.在平面直角坐标系中,直线 与x轴相交于点A , 与y轴相交于点C , 点B在x轴的负半轴上,且 ,抛物线经过点A , B , C , 点M为第一象限内抛物线上的一动点,过点M作直线 轴,交x轴于点 .
(1)求这条抛物线的函数表达式;
(2)如图1,当l经过抛物线顶点时,点D是抛物线对称轴上一点,若以C , B , D为顶点的三角形是等腰三角形,求点D坐标;
(3)如图2,连接 交y轴于点F , 连接 , ,若 的面积等于 的面积,求n的值.
14.如图,二次函数 的图象与 轴交于 , 与 轴交于点 .若点 , 同时从 点出发,都以每秒1个单位长度的速度分别沿 , 边运动,其中一点到达端点时,另一点也随之停止运动.
(1)求该二次函数的解析式及点 的坐标;
(2)当点 运动到 点时,点 停止运动,这时,在 轴上是否存在点 ,使得以 , , 为顶点的三角形为等腰三角形?若存在,请直接写出 点坐标;若不存在,请说明理由.
(3)当 , 运动到 秒时, 沿 翻折,点 恰好落在抛物线上 点处,请判定此时四边形 的形状,并求出 点坐标.
15.综合与探究
如图,在平面直角坐标系中,直线 与 轴交于点 ,与 轴交于点 .抛物线 经过 、 两点,且与 轴交于另一点 (点 在点 右侧).
(1)求抛物线的解析式及点 坐标;
(2)设该抛物线的顶点为点 ,则 ________;
(3)若点 是线段 上一动点,过点 的直线 平行 轴交 轴于点 ,交抛物线于点 .求 长的最大值及点 的坐标;
(4)在(3)的条件下:当 取得最大值时,在 轴上是否存在这样的点 ,使得以点 、点 、点 为顶点的三角形是等腰三角形?若存在,请直接写出所有点 的坐标;若不存在,请说明理由.
四、二次函数——直角三角形
16.如图,已知抛物线 ,与 轴交于点 和点 ,与 轴交于点 .
(1)求抛物线的解析式.
(2)坐标轴上是否存在点 ,使得 是直角三角形?若存在,求出点 的坐标:若不存在,说明理由.
17.如图10-1,以点 为顶点的抛物线与直线 交于 两点,且点A坐标为 ,点B在y轴上.
(1)求抛物线解析式;
(2)若点D是抛物线上位于直线 上方的一点(如图10-2),过点D作 轴于点E , 交直线 点F , 求线段 长度的最大值;
(3)在抛物线的对称轴 上是否存在点P , 使以点 为顶点的三角形是直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
18.如图,在平面直角坐标系中,已知抛物线 过A , B , C三点,点A的坐标是 ,点C的坐标是 ,动点P在抛物线上.
(1)求这个抛物线的解析式及顶点D的坐标;
(2)是否存在点P , 使得 是以 为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;
(3)设动点P的横坐标为m , 的面积为S.请直接写出面积S随着m的增大而减小时m的取值范围.
五、二次函数——等腰直角三角形(正方形)
19.如图,二次函数 的图象过点 ,交y轴于点C(0,-4).直线BO与抛物线相交于另一点D , 连接AB , AD , 点E是线段AB上的一动点,过点E作EF∥BD交AD于点F .
(1)求二次函数 的表达式;
(2)判断△ABD的形状,并说明理由;
(3)在点E的运动过程中,直线BD上存在一点G , 使得四边形AFGE为矩形,请判断此时AG与BD的数量关系,并求出点E的坐标;
(4)点H是抛物线的顶点,在(3)的条件下,点P是平面内使得∠EPF=90°的点在抛物线的对称轴上,是否存在点Q , 使得△HPQ是以∠PQH为直角的等腰直角三角形,若存在,直接写出符合条件的所有点Q的坐标;若不存在,请说明理由.
六、二次函数——平行四边形
20.如图,抛物线 的图象经过 三点,直线 经过点 ,交抛物线于点 .
(1)求抛物线的解析式;
(2)点 在线段 上,且满足 ,点 在 轴下方的抛物线上,设点 的横坐标为 ,当 为何值时, 的面积最大?并求出最大值;
(3) 为抛物线上的一动点, 为对称轴上一动点,若以 为顶点的四边形为平行四边形,求出点 的坐标.
21.如图,抛物线y= x2+bx+c与x轴交于点A和点B , 与y轴交于点C(0,﹣4),顶点为D , 其对称轴直线x=1交x轴于点P .
(1)求抛物线的解析式;
(2)如图1,线段MN的两端点M , N都在抛物线上(点M在对称轴左侧,点N在对称轴右侧),且MN=4,求四边形PMDN面积的最大值和此时点N的坐标;
(3)如图2,点Q是直线l:y=kx+1上一点,当以Q , A , C , B为顶点的四边形是平行四边形时,确定点Q的坐标和k的值.
22.如图,在平面直角坐标系中,抛物线 与x轴交于点 , ,与y轴交于点C.
(1)求该抛物线的解析式;
(2)直线l为该抛物线的对称轴,点D与点C关于直线l对称,点P为直线AD下方抛物线上一动点,连接PA,PD,求 面积的最大值;
(3)在(2)的条件下,将抛物线 沿射线AD平移 个单位,得到新的抛物线 ,点E为点P的对应点,点F为 的对称轴上任意一点,在 上确定一点G,使得以点D,E,F,G为顶点的四边形是平行四边形,写出所有符合条件的点G的坐标,并任选其中一个点的坐标,写出求解过程.
七、二次函数——矩形、菱形、正方形
23.如图,已知抛物线y=a +bx+3(a≠0)与x轴交于点A(1,0)和点B(-3,0),与y轴交于点C.
(1)求抛物线解析式;
(2)若M是抛物线对称轴上的一点,则△ACM周长的最小值为________;
(3)点N为第二象限抛物线上的动点,求△BCN面积的最大值及此时点N的坐标;
(4)点P是y轴上的一点,在坐标平面内存在点Q,使以A,C,P,Q为顶点的四边形是菱形,请直接写出点Q的坐标.
24.如图,抛物线 与x轴交于A , B两点(点A在点B左侧),与y轴交于点C .
(1)求A , B , C三点的坐标;
(2)连接 ,直线 与该抛物线交于点E , 与 交于点D , 连接 .当 时,求线段 的长;
(3)点M在y轴上,点N在直线 上,点P为抛物线对称轴上一点,是否存在点M , 使得以C、M、N、P为顶点的四边形是菱形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
25.综合与探究
如图,在平面直角坐标系中,抛物线 与x轴交于点A、B , 与y轴交于点C , 连接BC , ,对称轴为 ,点D为此抛物线的顶点.
(1)求抛物线的解析式;
(2)抛物线上C , D两点之间的距离是________;
(3)点E是第一象限内抛物线上的动点,连接BE和CE . 求 面积的最大值;
(4)点P在抛物线对称轴上,平面内存在点Q , 使以点B、C、P、Q为顶点的四边形为矩形,请直接写出点Q的坐标.
26.如图,抛物线 交x轴于 , 两点,交y轴于点C , 动点P在抛物线的对称轴上.
(1)求抛物线的解析式;
(2)当以P , B , C为顶点的三角形周长最小时,求点P的坐标及 的周长;
(3)若点Q是平面直角坐标系内的任意一点,是否存在点Q , 使得以A , C , P , Q为顶点的四边形是菱形?若存在,请直接写出所有符合条件的点Q的坐标;若不存在,请说明理由.
27.如图1,抛物线 与 轴交于 , 两点,与 轴交于点 .直线 经过抛物线上两点 , .已知点 , 的横坐标分别为 , 且满足 ,直线 的表达式为 .
(1)求 的值及抛物线的表达式;
(2)设点 是直线 上一动点,问:点 在什么位置上时, 的周长最小?求出点 的坐标及 周长的最小值;
(3)如图2, 是线段 上的一个动点,过点 作垂直于 轴的直线与直线 和抛物线分别交于点 , .若点 是直线 上一个动点,当点 恰好是线段 的中点时,在坐标平面内是否存在点 ,使以点 , , , 为顶点的四边形是菱形?若存在,请直接写出点 的坐标;若不存在,请说明理由.
答案解析部分
一、二次函数——周长线段之和最小
1.【答案】 (1)解:当y=0时, ,
解得x1=-4,x2=0,
点A(-4,0),
设直线 的函数解析式 ,过A、B两点,代入得
,
解方程组得 ,
直线 的函数解析式为 ;
(2)解:∵点 是抛物线的对称轴上的一个动点,抛物线对称轴为x= =-2,
∵C△BOQ的周长=OQ+QB+OB,点O,点B是定点,OB长是定值,
∴当 的周长最小时,就是OQ+QB最小,
∵点A与点O关于抛物线的对称轴对称,
∴点A,点Q,点B三点共线时,OQ+QB=AQ+QB≥AB最短,
当x =-2式, ,
点Q(-2,2),
S△BOQ的面积=S△BAO-S△QAO= ;
(3)(6,6)或(-2,6)或(-6,-6)
【解析】【解答】解:(3)以点A, , , 为顶点的四边形是平行四边形,分三种情况:
当以OB为对角线,四边形AONB为平行四边形,BN∥AO,且BN=AO,
设N1(x,y),
则y=6, x-4=2, x=6,
∴点N1(6,6);
当以AB为对角线,四边形AOBN为平行四边形是,NB∥AO,且NB=AO=4,
设N2(x,y),
则y=6, x+4=2, x=-2,
∴点N2(-2,6);
当以AO为对角线,四边形ANOB为平行四边形,AB∥ON,且AB=ON,
设N3(x,y),
∵6-0=0-y,2-0=-4-x,
∴y=-6, x=-6,
∴点N3(-6,-6);
∴以点A, , , 为顶点的四边形是平行四边形,则点 的坐标是(6,6)或(-2,6)或(-6,-6).
故答案为(6,6)或(-2,6)或(-6,-6).
【分析】(1)先求出 点A(-4,0), 再利用待定系数法求函数解析式即可;
(2)先求出 点A,点Q,点B三点共线时,OQ+QB=AQ+QB≥AB最短, 再求出 点Q(-2,2), 最后利用三角形的面积公式计算求解即可;
(3)分类讨论,结合图形,利用平行四边形的性质,列方程计算求解即可。
2.【答案】 (1)解:∵抛物线 与 轴分别交于点 和点 ,交 轴于点 ,
∴当 时, ,即 ,
当 时, , , ,即 , ,
设直线 的解析式为:
则 ,
∴ ,
∴直线 的表达式: .
(2)解:∵点 沿 以每秒1个单位长度的速度由点 向点 运动,
∴ , ,
∵ 轴,
∴ , ,
∴
∵ , ,
∴ , ,
∴△AOC是等腰直角三角形,
∴ ,由勾股定理得: ,
∵ 轴,
在 中, ,
∴△AEP也是等腰直角三角形,
∴ , ,
∴ ,
∴当 时,即 或 时, .
(3)解:在 中, ,
∴ ,
∴ 的周长: .
∴当 最小时 的周长最小.
当 时, 最小,
∵ ,
∴ ,
在 中, , , , ,
∴ ,
∴ ,
∴ .
【解析】【分析】(1)利用待定系数法进行求解即可;
(2)先求出 ,再求出 △AOC是等腰直角三角形, 最后进行求解即可;
(3)先求出 当 最小时 的周长最小 ,再求出 , 最后进行求解即可。
3.【答案】 (1)解:∵抛物线 与 轴相交于 , 两点, , ,
∴ ,
解得: ,
∴抛物线的解析式为:
(2)解:如图,过 作 轴于 ,交 于 ,
当 时, ,
∴ ,
设 的解析式为 ,则 ,
解得 ,
∴ 的解析式为: ,
设 ,则 ,
∴ ,
∵ 的面积是 ,
∴ ,
∴ ,
解得: 或3,
∵点 在直线 右侧的抛物线上,
∴ ,
∴ 的面积
(3)
(4)解:①当MB为对角线时,MN//BD,MN=BD,
过点N作NE⊥x轴于E,过当D作DF⊥x轴于F,
∵点D(3, ),
∴DF= ,
在△MNE和△BDF中, ,
∴△MNE≌△BDF,
∴DF=NE= ,
∵点D在x轴下方,MB为对角线,
∴点N在x轴上方,
∴点N纵坐标为 ,
把y= 代入抛物线解析式得: ,
解得: , ,
∴ ( , ), ( , )
如图,当BM为边时,MB//ND,MB=ND,
∵点D(3, ),
∴点N纵坐标为 ,
∴ ,
解得: , (与点D重合,舍去),
∴ ( , ),
综上所述:存在点 ,使得以点 , , , 为顶点的四边形是平行四边形,点 的坐标为: 或 或
【解析】【解答】(3)∵抛物线 与 轴相交于 , 两点,
∴点A与点B关于直线l对称,
∴BC为AP+CP的最小值,
∵B(4,0),C(0,-6),
∴AP+CP的最小值=BC= = .
故答案为:
【分析】(1)利用待定系数法求函数解析式即可;
(2)先求出 的解析式为: , 再求出 或3, 最后利用三角形的面积公式求解即可;
(3)先求出点A与点B关于直线l对称,再求出BC为AP+CP的最小值,最后利用勾股定理求解即可;
(4)分类讨论,利用全等三角形的性质与判定,再结合图象求解即可。
4.【答案】 (1)解:所给不等式组的解集为 , 其整数解为2,3.
∵OA,OB的长是所给不等式组的整数解,且OA
∵点A、B在抛物线上,
∴ ,解得, .
∴所求的抛物线的解析式为
∵点D(2,m)在抛物线上,
∴
(2)2
(3)9
(4)解:∵以A、B、M、N为顶点的四边形是菱形,对角线互相垂直且平分,
由∵
∴AB与MN不能作为一组对角线.
∴分两种情况:
①以AM与BN为对角线时,如图2①和图2②.
如图2①,AB=OA+OB=2+3=5,
∵四边形ABMN是菱形,
∴MN∥AB∥x轴,MN=MB=AB=5.
在 中,
∴M(0,4).
∴N(-5,4).
如图2②,同理可得:N(-5,-4).
②以AN与BM为对角线时,如图2③和图2④.
如图2③,菱形的边长仍为5,MN∥x轴,
∵
∴
∴
如图2④,同理可得:
综合上述①、②两种情况,符合条件的点N的坐标为:
【解析】【解答】(2)如图1所示,连接AD交y轴于点E , 则此时AE+ED最小.
设直线AD的解析式为
∵点A(-2,0),D(2,-4)在直线 AD上,
∴ ,解得, .
∴直线AD的函数解析式为
当x=0时,y=-2,.即E(0, -2).
∴
故答案为:2
(3)如图1,
∵AD//FB ,
∴
∴
∵
∴
∵
∴
∴
∴抛物线向上平移9个单位.
故答案为:9
【分析】(1)利用待定系数法求出 抛物线的解析式为 再计算求解即可;
(2)先求出直线AD的函数解析式为 再求出E(0, -2),最后计算求解即可;
(3)先求出再求出最后求解即可;
(4)分类讨论,结合图形,利用勾股定理求解即可。
二、二次函数——线段最值、面积倍数、最值
5.【答案】 (1)解:将A(﹣1,0),B(3,0)代入y=x2+bx+c,
得到
解得 ,
∴y=x2﹣2x﹣3
(2)解:将C点的横坐标x=2代入y=x2﹣2x﹣3,得y=﹣3,∴C(2,﹣3);
∴直线AC的函数解析式是y=﹣x﹣1.
设P点的横坐标为x(﹣1≤x≤2),则P、E的坐标分别为:P(x,﹣x﹣1),E(x,x2﹣2x﹣3);
∵P点在E点的上方,PE=(﹣x﹣1)﹣(x2﹣2x﹣3)=﹣x2+x+2,
=﹣(x )2 ,
∵﹣1<0,
∴当x 时,PE的最大值 ,此时P( , )
(3)解:存在.
理由:如图,设抛物线与y的交点为K,由题意K(0,﹣3),
∵C(2,﹣3),
∴CK∥x轴,CK=2,
当AC是平行四边形ACF1D1的边时,可得D1(﹣3,0).
当AC是平行四边形AF1CD2的对角线时,AD2=CK,可得D2(1,0),
当点F在x轴的上方时,令y=3,3=x2﹣2x﹣3,
解得x=1± ,
∴F3(1 ,3),F4(1 ,3),
由平移的性质可知D3(4 ,0),D4(4 ,0).
综上所述,满足条件的点D的坐标为(﹣3,0)或(1,0)或(4 ,0)或(4 ,0).
【解析】【分析】
(1)将A、B两点坐标代入抛物线解析式,可以得到关于b和c的方程组,解方程组求出b和c,然后写出解析式即可;
(2)将点 点C(2,m) 代入解析式求出坐标,直线经过A、C两点,利用待定系数法求出直线解析式,设P点横坐标为x,利用直线AC解析式表示出纵坐标,E点横坐标也为x,纵坐标代入抛物线解析式表示出来,然后PE=两点纵坐标之差,整理出表达式,再求最值及点P的坐标即可;
(3)分情况讨论,四点中只有点A与点C是固定的,分别确定当AC为一边,当AC为对角线时,平行四边形的几种位置,然后计算的坐标。
6.【答案】 (1)y=﹣x2+2x+3
(2)解:设直线AC的解析式为y=mx+n,把A(﹣1,0),C(2,3)代入得,
,
解得, ,
直线AC的解析式为y=x+1,
依题意得,P(t,﹣t2+2t+3),M(t,t+1),
PM=﹣t2+2t+3-(t+1)= ﹣t2+t+2=-(t- )2+ ,
当t= 时,PM有最大值,最大值为
(3)解:∵y=﹣x2+2x+3=﹣(x﹣1)2+4
∴顶点D(1,4),把x=1代入y=x+1得,y=2,
∴B(1,2),BD=2,
设点E(m,m+1),则F(m,﹣m2+2m+3),EF= ,
∵EF∥BD,
∴当EF=BD时,以B,D,E,F为顶点的四边形能为平行四边形.
∴ =2,
当 时,
解得:m1=0,m2=1(舍去),
当 时,
解得m3= ,m4= ;
∴点E的坐标为:(0,1)或( , )或( , ).
【解析】【解答】解:(1)把A(﹣1,0),C(2,3)代入y=﹣x2+bx+c得,
,
解得, ,
抛物线的解析式为:y=﹣x2+2x+3;
故答案为:y=﹣x2+2x+3;
【分析】(1)先求出 , 再求函数解析式即可;
(2)利用待定系数法求出直线AC的解析式为y=x+1,再求解即可;
(3) 先求出 =2, 再分类讨论求解即可。
7.【答案】 (1)解:将点 、 的坐标代入抛物线表达式得 ,
解得 ,
∴抛物线的表达式为:
(2)解:由抛物线的表达式知,点 ,
设直线 的表达式为: ,
, ,
则 ,
解得: ,
直线 的表达式为: ;
设点 ,则点 ,点 ,
∴ ,
∵ ,故 ,
∴ ,
∴ ,
∵ ,
∴当 时, 有最大值为 ;
(3)解:存在,理由:
点 、 的坐标分别为 、 ,
则 ,过点 作 轴于点 ,
①当 时,
在 中, 由勾股定理得 ,
即 ,
解得: , (舍去),
故点 ;
②当 时,则 ,连接 .
在 中, 由勾股定理得 .
即 ,
解得: , (舍去),
则 ,
故点 ;
③当 时, ,
即 ,
解得: ;
则 ,
故点 ,
综上,点 的坐标为 或 或 .
【解析】【分析】(1)先求出a=-1,b=3,再求抛物线的解析式即可;
(2)利用待定系数法求出直线 的表达式为: ,再利用特殊角的锐角三角函数值计算求解即可;
(3)分类讨论,结合图象,利用勾股定理计算求解即可。
8.【答案】 (1)解:将点A、B的坐标代入抛物线表达式得 ,
解得 ,
故抛物线的表达式为y=﹣x2+2x+3,
当x=0时,y=3,故点C(0,3);
(2)解:当m=1时,点E(1,0),设点D的坐标为(1,a),
由点A、C、D的坐标得,AC= ,
同理可得:AD= ,CD= ,
①当CD=AD时,即 = ,解得a=1;
②当AC=AD时,同理可得a= (舍去负值);
故点D的坐标为(1,1)或(1, );
(3)解:∵E(m,0),则设点M(m,﹣m2+2m+3),
设直线BM的表达式为y=sx+t,则 ,
解得: ,
故直线BM的表达式为y=﹣ x+ ,
当x=0时,y= ,故点N(0, ),则ON= ;
S1= AE×yM= ×(m+1)×(﹣m2+2m+3),
2S2=ON xM= ×m=S1= ×(m+1)×(﹣m2+2m+3),
解得m=﹣2± (舍去负值),
经检验m= ﹣2是方程的根,
故m= ﹣2.
【解析】【分析】(1)将点A、B的坐标代入抛物线表达式得 , 解得即可得到抛物线的表达式;
(2)当m=1时,点E(1,0),设点D的坐标为(1,a), 由点A、C、D的坐标得,AC= ,同理可得:AD= ,CD= ,①当CD=AD时;②当AC=AD时,可得点D的坐标为(1,1)或(1, );
(3)S1= AE×yM,2S2=ON xM,即可求解。
9.【答案】 (1)解: 抛物线 过点 和 ,
解得
抛物线的解析式为 .
令 ,得 .
解得 , .
点 的坐标为 .
设直线 的解析式为 .
把点 , 分别代入 ,得
解得
直线 的解析式为
(2)解:如图,设抛物线的对称轴 与 轴交于点 .
抛物线的解析式为 ,
顶点 的坐标为 .
四边形 四边形
.
(3)解: .
.
如图,过点 作 轴,交 轴于点 ,交 于点 .
设点 .
点 在直线 上,
.
.
.
.
解得 , .
,
(4)解:存在.
直线 的解析式为
对称轴 为:
①当 时,点M与点H重合,
②当 时,
或者
③当 时, ,
点 的坐标为 或 或 或
【解析】【分析】(1)利用待定系数法求出抛物线的解析式为 ,再求出 点 的坐标为 ,最后求函数解析式即可;
(2)先求出顶点 的坐标为 ,再利用三角形的面积公式和四边形面积公式计算求解即可;
(3) 先求出 ,再求出 ,最后计算求解即可;
(4)先利用勾股定理求出BE的值,再分类讨论,求点的坐标即可。
10.【答案】 (1)解:∵OB=OC=3OA,AC= ,
∴ ,即 ,
解得:OA=1,OC=OB=3,
∴A(1,0),B(-3,0),C(0,3),代入 中,
则 ,解得: ,
∴抛物线的解析式为
(2)解:如图,四边形PBAC的面积=△BCA的面积+△PBC的面积,
而△ABC的面积是定值,故四边形PBAC的面积最大,只需要△BPC的最大面积即可,
过点P作y轴的平行线交BC于点H,
∵B(-3,0),C(0,3),设直线BC的表达式为y=mx+n,
则 ,解得: ,
∴直线BC的表达式为y=x+3,
设点P(x,-x2-2x+3),则点H(x,x+3),
S△BPC= = = ,
∵ ,故S有最大值,即四边形PBAC的面积有最大值,
此时x= ,代入 得 ,
∴P( , )
(3)解:若BP为平行四边形的对角线,
则PQ∥BM,PQ=BM,
则P、Q关于直线x=-1对称,
∴Q( , );
若BP为平行四边形的边,
如图,QP∥BM,QP=BM,
同上可得:Q( , );
如图,BQ∥PM,BQ=PM,
∵点Q的纵坐标为 ,代入 中,
解得: 或 (舍),
∴点Q的坐标为( , );
如图,BP∥QM,BP=QM,
∵点Q的纵坐标为 ,代入 中,
解得: (舍)或 ,
∴点Q的坐标为( , );
综上:点Q的坐标为( , )或( , )或( , )
【解析】【分析】(1)由已知易求得OA、OC=OB的值,于是可得点A、B、C的坐标,用待定系数法可求抛物线的解析式;
(2)由图知:S四边形PBAC=S△BCA+S△PBC , 而△ABC的面积是定值,所以要使四边形PBAC的面积最大,只需要△BPC的最大面积即可;结合二次函数的性质可求解;
(3)由题意可分三种情况讨论:
①若BP为平行四边形的对角线,则PQ∥BM,PQ=BM,则P、Q关于直线x=-1对称,于是可得点Q的坐标;
②若BP为平行四边形的边,则BQ∥PM,BQ=PM,同理可求解;
③若BP为平行四边形的边,则 BP∥QM,BP=QM,同理可求解.
11.【答案】 (1)解:∵点 , 在抛物线 上,
∴将 , 代入解析式,
得 ,
∴ ,
∴抛物线的二次函数解析为
(2)解:运用平行四边形对角线互相平分的性质和中点坐标公式求解,
设点 , ,
①当 为对角线时,则 ,即 ,
代入得 ,
解得 或 ,
∴得点 , ;
②当 为对角线时,则 ,
同理求得点 ,
③当 为对角线时,则
同理求得点 与点 重合,即 ;
综上所述, , ,
(3)解:如图,过点C作x轴的平行线,交 于点M;过点H作y轴的平行线,交 于点E,交 于点F,交x轴于点G.
设点H的坐标为 ,
∵ , ,
∴直线 的解析式为 ,
∴点F的坐标为 .
∵ , ,
∴直线 的解析式为 ,
∴点M的坐标为 .
求 的面积表达式有以下二种方法:
解法1:水平分割时,
.
当 时, 的面积最大,此时 ;
解法2:垂直分割时,
,
当 时,面积最大,此时 ,
解法3:如图下图,过点H作 的平行线l,
∵直线 的解析式为 ,直线l与直线平行,
∴直线l解析式的k=1,
∴设直线l的解析式为 ,
当直线l与抛物线相切时, 面积最大,
由 ,
消去y,得: ,①
当方程①的 时,直线l与抛物线相切,
, ,
∴ 为所求.
【解析】【分析】(1)把点 , 在抛物线 得抛物线为 ;
(2)①当 为对角线时,②当 为对角线时,③当 为对角线时,分三种情况讨论即可;
(3)设点H的坐标为 , , 由B、C的坐标得出直线 的解析式,由B、H的坐标得出直线 的解析式,即可得到点M的坐标,可利用水平分割、垂直分割两种方法都可求出 的面积表达式,由此得出当 的面积最大时,求出H的坐标。
三、二次函数——等腰三角形
12.【答案】 (1)解:∵C(0,4),∴OC=4.
∵OA=OC=4OB,∴OA=4,OB=1,
∴A(4,0),B( 1,0),
设抛物线解析式:y=a(x+1)(x 4),
∴4= 4a,∴a= 1.
∴y= x2+3x+4.
(2)解:存在.
作PN⊥x轴交AC于N,
AC的解析式为y=-x+4 ,
设P(x, x2+3x+4),则N(x,-x+4),
得PN=( x2+3x+4)-(-x+4)= x2+4x ,
∴S△PAC= PN×4=2PN=2( x2+4x)=-2(x-2)2+8 ,
当x=2时,ΔPAC面积的最大值为8,此时点P的坐标为(2,6).
∴P点坐标为(2,6)时,ΔPAC面积有最大值,最大面积是8 .
(3)Q(0,0),(-4,0),
【解析】【解答】解:(3) 设 根据勾股定理得:
①当 时,
此时可得Q的坐标为(4+4 ,0)、(4-4 ,0);
②当 时,
当 时,不合题意舍去,
③当 时,
综上,符合条件的点Q的坐标为:(0,0),(-4,0), .
【分析】(1)由C的坐标,得出OC的值,由OA=OC=4OB,得出OA=4,OB=1,以及A、B的坐标,设抛物线解析式:y=a(x+1)(x 4),解出a的值,即可得出抛物线的函数表达式;
(2)存在,作PN⊥x轴交AC于N,由A和C的坐标,得出AC的解析式,设P(x, x2+3x+4),则N(x,-x+4),得PN=( x2+3x+4)-(-x+4)= x2+4x ,得出S△PAC的值,当x=2时,ΔPAC面积的最大值为8,此时点P的坐标为(2,6).
(3)设 根据勾股定理得出 , ①当 时,②当 时,③当 时,三种情况分析即可得到点Q的坐标。
13.【答案】 (1)解:对于y=﹣x+3,令y=﹣x+3=0,解得x=3,令x=0,则y=3,
得,点A的坐标为(3,0),点C的坐标为(0,3),
∵AB=4,点B在x轴的负半轴上,
∴点B的坐标为(﹣1,0),
∵抛物线经过点A(3,0),C(﹣1,0),
∴设抛物线的解析式为y=a(x﹣3)(x+1),
将C(0,3)代入,得a=﹣1,
∴抛物线的解析式为y=﹣(x﹣3)(x+1),
即:y=﹣x2+2x+3;
(2)解:由题意得:BC= ,设D(1,m),
①当BD=CD时,BD2=CD2 ,
即:22+m2=12+(3﹣m)2 ,
解得:m=1,
∴D1(1,1);
②当BD=BC时,4+m2=10,解得 ,
∴ , ;
③当CD=BC时,1+(m﹣3)2=10,
解得:m1=6(舍去),m2=0,
∴D4(1,0);
综上所述,满足条件的D点的坐标是:D1(1,1), , ,D4(1,0);
(3)解:点M的坐标为(n,﹣n2+2n+3),
由题意得:tan∠MBN ,
∴OF 3﹣n,
∵S△MAN=S△MOF ,
∴ AN MN OF xM , 即 (3﹣n)(﹣n2+2n+3) (3﹣n)n,
即:﹣n2+2n+3=n,
解得: , (舍去),
∴n .
【解析】【分析】(1)由待定系数法即可求解;
(2)分BD=CD、BD=BC、CD=BC三种情况,分别求解即可;
(3)由S△MAN=S△MOF, 得到 AN MN OF xM, 即可求解。
14.【答案】 (1)解:∵二次函数 的图象与 轴交于 , ,
∴ , ,
∴ ,
∴该二次函数的解析式为 ,
当 时, ,
∴ ;
(2)解:如图1,存在满足条件的点 ,
∵ , ,
∴ ,
当点 运动到 点时,此时 ,
∴存在以下3种情况:
图1
①当 时,
∵ ,
∴ ,
∴ ,
∴点 坐标 ;
② ,此时 ,
∴ ,
∴ ,
∴点 坐标 ;
③当 时,
设此时 的坐标为 ,
则 ,
解得, 或 ,
∴ 或 ,
综上所述:点 坐标为 、 或 或 ;
(3)解:四边形 为菱形,
图2
如图2, 点关于 与 点对称,过点 作 于 ,
∵ , 沿 翻折,点 恰好落在抛物线上 点处,
∴ ,
∴平行四边形 为菱形,且 ,
∵ ,
∴ , ,
又∵ ,
∴ ∽ ,
∴ ,
∴ ,
∴ , ,
∴ ,
∵ ,
∴ ,
∵点 在二次函数 上,
代入解得 ,
∴ .
【解析】【分析】(1)根据韦达定理即可求得 、 的值,即可得到该二次函数的解析式,然后令 ,即可得到点 的纵坐标,此题得解;(2)由题目已知条件可知,存在满足条件的点 ,根据已知条件以及第(1)问可得 ,分以下三种情况分别讨论即可:① ;② ;③ ,即可得到点 的坐标;(3)如图2, 点关于 与 点对称,过点 作 于 ,根据题目已知条件以及翻折的意义可知四边形 为菱形;根据 可得 ∽ ,根据相似比即可求得 、 的值(用 表示),即可求得点 的坐标(用 表示),根据 ,即可求得点 的坐标(用 表示),再根据 在二次函数 上,即可求得 的值,进而可得点 的坐标.
15.【答案】 (1)∵直线y=-3x-3与x轴、y轴分别交于点A、C,
当 时,
∴
当 时,
∴
∵抛物线y=x2+bx+c经过点A、C,
∴
∴
∴抛物线的解析式是:
当 时,
解得:
∴
(2)3
(3)由(1)知 , 直线 的解析式是:
设 ,则
∴
当 时, 的最大值
∴点 的坐标为
(4)存在,如图,
由(2)得,当ME最大时,则D( ,0),M( , ),
∴DO=DB=DM= ;
∵∠BDM=90°,
∴OM=BM= .
点P1、P2、P3、P4在x轴上,
当点P1与原点O重合时,则P1M=BM= ,P1(0,0);
当BP2=BM= 时,则OP2= ,
∴P2( ,0);
当点P3与点D重合时,则P3M=P3B= ,
∴P3( ,0);
当BP4=BM= 时,则OP4= ,
∴P4 .
综上所述, .
【解析】【解答】设抛物线的对称轴交BC于点F , 交x轴于点G .
设直线BC的解析式为y=kx-3,则3k-3=0,解得k=1,
∴y=x-3;
∵y=x2-2x-3=(x-1)2-4,
∴抛物线的顶点H(1,-4),
当x=1时,y=1-3=-2,
∴F(1,-2),
∴FH=-2-(-4)=2,
∴ .
故答案为:3.
【分析】(1)直线y=-3x-3与x轴、y轴分别交于点A、C,当 时, , 当 时, , 得出A、C的坐标,因为抛物线y=x2+bx+c经过点A、C,得出b、c的值,即可得出抛物线的解析式,当 时, , 解得即可得出B的坐标;
(2)设抛物线的对称轴交BC于F点,求得直线BC的解析式,即可得出k=1,得到抛物线的顶点H,当x=1时,y=1-3=-2,即可求得 的面积;
(3)由(1)知 , 直线 的解析式是: , 设 , 则 , 当 时, 的最大值 , 即可得出点 的坐标;
(4)当点P1与原点O重合、当BP2=BM= 、当点P3与点D重合、当BP4=BM= 时,分情况讨论即可得出答案。
四、二次函数——直角三角形
16.【答案】 (1)解:根据题意得,
解得: ,
所以抛物线的解析式为:
(2)解:存在
分3种情况讨论:
①若 ,此时点 与原点 重合,所以
②若 ,过点 作 交 轴于点
∴ , ,
∴
∴
∴ ,即
∴ ,故
③若 ,过点 作 交 轴于点
∴ , ,
∴
∴
∴ ,即
∴ ,故
综上:存在点 , , 满足题意.
【解析】【分析】(1)将点A、B、C的坐标代入函数解析式,利用待定系数法求解即可;
(2)分情况讨论,结合函数图象,利用相似三角形的性质分别求解即可。
17.【答案】 (1)解:设抛物线的解析式为
顶点
把 代入解析式得:
抛物线的解析式 ;
(2)解:
设 ,则F的坐标为
当 时, 有最大值为2;
(3)解:存在,
①过点A作 于点
点 在对称轴直线 上
设 的坐标为
点A的坐标为
点 的坐标为
②过点A作 于点A,交直线 于点
于点A
于点
点 在对称轴直线 上
设 的坐标为
解此方程得:
点 的坐标为
综上所述,点P的坐标分别为 或 .
【解析】【分析】(1)设抛物线的解析式为 , 由顶点 , 得出 , 把 代入解析式得: , 由此得出a的值,即可得出抛物线解析式;
(2)由解析式得出 , 设 , 则F的坐标为 , 得出 , 当 时, 有最大值为2;
(3)存在,①过点A作 于点 , 由点 在对称轴直线 上,可设 的坐标为 , 因为 点A的坐标为 , 得出m的值,由此得出的坐标;②过点A作 于点A,交直线 于点 , 由 于点A,得出 , , 得出 , , 因为 , 点 在对称轴直线 上,得出设 的坐标为 , , , 解此方程得: , 得出点 的坐标为 。
18.【答案】 (1)解:将点A、C的坐标代入抛物线表达式得:
∴
∴此抛物线的解析式 .
∵ ,
∴顶点D的坐标为 ;
(2)解:存在;
①当 时:(如图1)
∵ ,
∴ .
∴ ,
∴ ,即
∴ , (舍)
∴ ;
②当 时:(如图2)
∵ ,
∴ ,
∴ ,即 .
∴ , (舍)
∴ .
∴符合条件的点P的坐标为 或 ;
(3) 或
【解析】【解答】解:(3)由图象可得 时, 的面积为S随着m的增大而减小;
∵顶点D的坐标为 ,点A的坐标是 ,
∴由图象可得 时,过点P作 轴交 于点N ,
设直线 的解析式 ,
∵点A的坐标是 ,点C的坐标是 ,
∴线 的解析式 ,
设点P的坐标是 ,则点 ,
∴ 的面积为 ,
当 时, 的面积有最大值,
∴ 时,S随着m的增大而减小.
∴面积S随着m的增大而减小时m的取值范围为 或 .
【分析】(1)先求出 再求出 此抛物线的解析式 ,最后求点的坐标即可;
(2)分类讨论,作图求解即可;
(3)先求出直线 的解析式 ,再利用三角形的面积公式进行计算求解即可。
五、二次函数——等腰直角三角形(正方形)
19.【答案】 (1)解:∵二次函数 的图象经过点A、点C,
∴ ,解得 .
∴二次函数的解析式为 .
(2)解:△ABD是直角三角形.理由如下:
∵点B(-2,m)在抛物线 上,
∴m= .
∴B(-2,-1).
∴直线OB的解析式为: ,
联立 ,解得: (即B点)或 ,
∴D(8,4),
∵A(4,-4),
∴由两点间距离公式得:
, , ,
∵ ,
∴△ABD是以BD为斜边的直角三角形;
(3)解:如图所示,
∵四边形AFGE为矩形,
∴EG∥AD,FG∥AB,
∵EF∥BD,
∴四边形EFDG和四边形FEBG都是平行四边形,
∴EF=GD,EF=BG,
∴BG=GD,
由(2)得△ABD为直角三角形,
∴AG= BD,
∵EG∥AD,
∴点E是AB的中点,
∴E ;
(4)存在,Q(2,﹣4)或(2, )
【解析】【解答】解:(4)如图,设EF的中点为K , P(x , y),连接PK ,
∵EF∥BD ,
∴ ,
又∵ ,
∴AF=FD , F为AD的中点,
由中点坐标公式可得,F(6,0),E ,
∵K为EF的中点,
∴K ,
根据两点间的距离公式可得: ,
∵∠EPF=90°,
∴点P在以K为圆心,EF为直径的圆上运动,
∵△PQH为等腰直角三角形,∠PQH=90°,
∴∠QHP=45°,
∴PQ∥x轴,
∴直线PH可看做由直线y=x平移得到,
则设直线PH的解析式为:y=x+b ,
∵抛物线的顶点为H(2,-5),
∴代入PH解析式得:b=-7,
∴直线PH的解析式为:y=x-7,
∵PK= EF ,
∴ ,
即: ,
解得: 或 ,
∵PQ∥x轴,
∴Q(2,﹣4)或(2, ).
【分析】(1)利用待定系数法计算求解即可;
(2)先求出直线OB的解析式为: , 再求出 , , , 最后求解即可;
(3)先求出四边形EFDG和四边形FEBG都是平行四边形,再求出点E是AB的中点,最后求点的坐标即可;
(4) 利用中点坐标公式,两点间的距离公式和勾股定理进行计算求解即可。
六、二次函数——平行四边形
20.【答案】 (1)解:∵抛物线 的图象经过点 ,
∴设抛物线的解析式为 .
把点 代入,
.
.
∴抛物线的解析式为 .
(2)解:∵直线 经过点 ,
.
∴直线 的解析式为 .
联立
解得 ,
∴点
.
设点 .
,
.
.
.
∴点 .
∴直线 的解析式为 .
如图,过点 作 轴交直线 于点 .
∵点 ,
.
设点B的横坐标为xB , 点E的坐标为xE ,
.
∴当 时,
有最大值为 .
(3)解:∵ ,
∴点Q的横坐标为2,
设点A,D,P,Q的横坐标分别为xA,xD,xP,xQ ,
若 为平行四边形的边,
∵以 为顶点的四边形为平行四边形,
.
或 .
或 .
∴点 的坐标为 或 ;
若 为平行四边形的对角线,
∵以 为顶点的四边形为平行四边形,
与 互相平分.
.
.
∵点 的坐标为 .
综上,当点 的坐标为 或 或 时,以 为顶点的四边形为平行四边形.
【解析】【分析】(1)将已知点的坐标代入二次函数的解析式,利用待定系数法确定二次函数的解析式即可;
(2)联立方程,解之即得出D的坐标,得出三角形ABD的面积,设点 . 因为 , 得到m的值,即得到直线 的解析式,过点 作 轴交直线 于点 . 设点B横坐标为xB, 点E的坐标为xE, 求出三角形FBE的面积,当 时, 有最大值;
(3)设点A,D,P,Q的横坐标分别为xA,xD,xP,xQ, 若 为平行四边形的边,得出 . 得出P的坐标,若 为平行四边形的对角线,得出 与 互相平分.分情况讨论即可。
21.【答案】 (1)解:由题意得: ,解得 ,
故抛物线的表达式为y= x2﹣x﹣4;
(2)解:由抛物线解析式得点D坐标为(1,﹣ ),
设四边形PMDN面积为S,
则S=S△PDM+S△PDN= PD(xN﹣xM)= (xN﹣xM),
故当MN与轴平行时,此时MN=4,S的面积最大,
则S=9,
此时点M、N关于抛物线对称轴对称,则点N的横坐标为3,
当x=3时,y= x2﹣x﹣4=﹣2.5,
故点N的坐标为(3,﹣2.5);
(3)解:把y=0代入y= x2﹣x﹣4得 x2﹣x﹣4=0,
解得: ,
∴点A(-2,0),点B(4,0)
设点Q的坐标为(m,km+1),
当AC为边时,如图1,
点A向右平移2个单位向下平移4个单位得到点C,同样点B向右平移2个单位向下平移4个单位得到点Q,
即 解得 ,
故点Q的坐标和k分别为(6,﹣4)、﹣ ;
如图2,
点A向右平移2个单位向下平移4个单位得到点C,同样点Q向右平移2个单位向下平移4个单位得到点B,
即 ,解得 ,
故点Q的坐标和k分别为(2,4)、1.5;
当AC是对角线时,
由中点公式得 解得 ,
故点Q的坐标和k分别为(﹣6,﹣4)、﹣ ;
综上,点Q的坐标和k分别为(6,﹣4)、﹣ 或(2,4)、1.5或(﹣6,﹣4)、﹣ .
【解析】【分析】(1)用待定系数法即可求解;
(2)由S=S△PDM+S△PDN= PD(xN﹣xM)= (xN﹣xM),即可求解;
(3)分AC为边、AC是对角线两种情况,利用图象平移和中点公式,分别求解即可.
22.【答案】 (1)解:将A(-1,0),B(4,0)代入y=ax2+bx-4得
,解得: ,
∴该抛物线的解析式为y=x2-3x-4,
(2)解:把x=0代入y=x2-3x-4中得:y=-4,
∴C(0,-4),
抛物线y=x2-3x-4的对称轴l为
∵点D与点C关于直线l对称,
∴D(3,-4),
∵A(-1,0),
设直线AD的解析式为y=kx+b;
∴ ,解得: ,
∴直线AD的函数关系式为:y=-x-1,
设P(m,m2-3m-4),
作PE∥y轴交直线AD于E,
∴E(m,-m-1),
∴PE=-m-1-(m2-3m-4)=-m2+2m+3,
∴ ,
∴ ,
∴当m=1时, 的面积最大,最大值为:8
(3)解:∵直线AD的函数关系式为:y=-x-1,
∴直线AD与x轴正方向夹角为45°,
∴抛物线沿射线AD方向平移平移 个单位,相当于将抛物线向右平移4个单位,再向下平移4个单位,
∵ , ,平移后的坐标分别为(3,-4),(8,-4),
设平移后的抛物线的解析式为
则 ,解得: ,
∴平移后y1=x2-11x+20,
∴抛物线y1的对称轴为: ,
∵P(1,-6),
∴E(5,-10),
∵以点D,E,F,G为顶点的四边形是平行四边形,分三种情况:
设G(n,n2-11n+20),F( ,y),
①当DE为对角线时,平行四边形的对角线互相平分
∴ ,∴
∴
②当EF为对角线时,平行四边形的对角线互相平分
∴ ,∴
∴
③当EG为对角线时,平行四边形的对角线互相平分
∴ ,∴
∴
∴ 或 或
【解析】【分析】(1)利用待定系数法,由点A,B的坐标求出函数解析式.
(2)由x=0求出对应的y的值,可得到点C的坐标,利用函数解析式求出抛物线的对称轴,利用轴对称的性质可求出点D的坐标;再利用待定系数法求出直线AD的解析式 , 设P(m,m2-3m-4), 作PE∥y轴交直线AD于E, 同时可表示出点E的坐标及PE的长,然后利用三角形的面积公式可得到△APD的面积与m之间的函数解析式,将其函数解析式转化为顶点式,利用二次函数的性质,可求出结果.
(3) 直线AD与x轴正方向夹角为45°,抛物线沿射线AD方向平移平移 个单位,相当于将抛物线向右平移4个单位,再向下平移4个单位,利用待定系数法求出平移后的函数解析式,同时可求出 抛物线y1的对称轴及点E的坐标;以点D,E,F,G为顶点的四边形是平行四边形,分三种情况:设G(n,n2-11n+20),F( ,y),①当DE为对角线时,平行四边形的对角线互相平分;②当EF为对角线时,平行四边形的对角线互相平分;③当EG为对角线时,平行四边形的对角线互相平分;分别利用线段的中点坐标建立关于n的方程,解方程求出n的值,即可得到点G的坐标.
七、二次函数——矩形、菱形、正方形
23.【答案】 (1)解:根据题意,得 ,
解方程组,得 ,
∴抛物线的解析式为y=﹣ ﹣2x+3
(2) +
(3)解:如图,过点N作直线NE⊥x轴,垂足为M,交直线BC于点E,
设直线BC的解析式为y=kx+n,
∵B(-3,0),C(0,3),
∴ ,
解方程组,得 ,
∴直线BC解析式为y=x+3,
设N(n,﹣ -2n+3),E(n,n+3),
∴NE=﹣ -2n+3-n-3=﹣ -3n,
∴ = + = +
= =﹣ - = ,
∴△BCN面积最大值 ,
此时,x= ,y= ,
故点
(4)解:如图,当AC为菱形的边时,
∵CP∥A ,AC= = ,
∴A = ,
∵A(1,0),
∴ (1, )或 (1,- );
当AC为菱形的对角线时,
设 (0,m),
∴A = ,C =3-m,
∴ ,
解得m= ,
∴C =3-m= ,
∴A = ,
∴ (1, );
当CP为菱形的对角线时,
作出点A关于CP的对称点即可,
∵A(1,0),
∴ (-1,0),
综上所述,点Q的坐标为(-1,0)或(1, )或(1, )或(1,- ).
【解析】【解答】(2)∵A , B是对称点,
∴抛物线的对称轴与BC的交点为△ACM周长最小位置,且最小值为BC+AC ,
∵A(1,0),B(-3,0),C(0,3),
∴AC= = ,BC= = ,
∴△ACM周长最小值为 + ,
故答案为: + ;
【分析】(1)利用待定系数法求函数解析式即可;
(2)先求出AC= = ,BC= = ,再计算求解即可;
(3)先求出直线BC解析式为y=x+3, 再求出 △BCN面积最大值 , 最后求点的坐标即可;
(4)分类讨论,利用勾股定理计算求解即可。
24.【答案】 (1)解:令x=0得 ,∴C点坐标(0,-8)
令y=0得:
解得:
∴A(-4,0),B(2,0)
(2)解:设DE交x轴于F,
设AC解析式为 ,代入AC坐标得:
,解得
∴AC解析式为
∵直线 与该抛物线交于点E,与 交于点D
∴
∴
∵
∴
∴
∴
∴
解得
∴
(3)解:抛物线 对称轴为
∵点M在y轴上,点N在直线 上,点P为抛物线对称轴上一点
∴设
当CM菱形的边时,则CM∥PN,CM=CN
∴N在对称轴上,即
∴
∴
解得
此时M点坐标为
当CM为菱形的对角线时,此时NP关于CM对称,即NP关于y轴对称
∴
∴
∵菱形对角线互相垂直平分
∴NP中点与CM中点是同一个点
∴
解得
此时M点坐标为
综上所述,存在M 、 使得以C、M、N、P为顶点的四边形是菱形.
【解析】【分析】(1)先求出 ,再求出 ,最后求点的坐标即可;
(2)先求出 AC解析式为 ,再求出 ,最后求解即可;
(3)先求出 ,再求出 ,最后求点的坐标即可。
25.【答案】 (1)解: 抛物线 的对称轴为 ,
,
,
,且点A在x轴负半轴上,
,
将点 代入 得: ,解得 ,
则抛物线的解析式为 ;
(2)
(3)解:如图,过点E作x轴的垂线,交 于点F,
,抛物线的对称轴为 ,
,
设直线 的解析式为 ,
将点 代入得: ,解得 ,
则直线 的解析式为 ,
设点E的坐标为 ,则 , ,
,
,
,
由二次函数的性质得:在 内,当 时, 取最大值,最大值为 ,
即 面积的最大值为 ;
(4) 或 或 或
【解析】【解答】解:(2) 化成顶点式为 ,
则顶点D的坐标为 ,
当 时, ,即 ,
则抛物线上 两点之间的距离是 ,
故答案为: ;
(4)设点P的坐标为 ,
由题意,分以下三种情况:
①当 为矩形 的边时,则 ,
设直线 的解析式为 ,
将点 代入得: ,
则直线 的解析式为 ,
将点 代入得: ,即 ,
将点C先向右平移2个单位长度,再向上平移4个单位长度可得到点P,
四边形 是矩形,
点C平移至点P的方式与点B平移至点Q的方式相同,
,
,即 ;
②当 为矩形 的边时,则 ,
同(4)①的方法可得:点Q的坐标为 ;
③当 为矩形 的对角线时,则 ,
,
即 ,
解得 或 ,
或 ,
当点P的坐标为 时,
则将点P先向左平移2个单位长度,再向下平移 个单位长度可得到点C,
四边形 是矩形,
点P平移至点C的方式与点B平移至点Q的方式相同,
,即 ;
同理可得:当点P的坐标为 时,点Q的坐标为 ,
综上,点Q的坐标为 或 或 或 .
【分析】(1)先求出点A的坐标,再求出 , 最后求函数解析式即可;
(2)先求出顶点D的坐标为 ,再求出 ,最后利用两点间的距离公式进行求解即可;
(3)利用待定系数法求出直线 的解析式为 , 再利用三角形的面积公式计算求解即可;
(4)分类讨论,利用矩形的性质、勾股定理、平移和点的坐标进行求解即可。
26.【答案】 (1)解:将 , 代入二次函数表达式中,
∴ ,解得 ,
∴二次函数的表达式为: ;
(2)解:连接BP、CP、AP,如下图所示:
由二次函数对称性可知,BP=AP,
∴BP+CP=AP+CP,
BC为定直线,当C、P、A三点共线时, 有最小值为 ,
此时 的周长也最小,
设直线AC的解析式为: ,代入 ,
∴ ,解得 ,
∴直线AC的解析式为: ,
二次函数的对称轴为 ,代入 ,得到 ,
∴P点坐标为(1,2),
此时 的周长最小值= ;
(3)解:Q点坐标存在,为(2,2)或(4, )或(4, )或( , )或( , )
【解析】【答案】解:(3) 设P点坐标为(1,t),Q点坐标为(m , n),
分类讨论:
情况一:AC为菱形对角线时,另一对角线为PQ ,
此时由菱形对角互相平分知:AC的中点也必定是PQ的中点,
由菱形对角线互相垂直知: ,
∴ ,解得 ,
∴P点坐标为(1,1),对应的Q点坐标为(2,2);
情况二:AP为菱形对角线时,另一对角线为CQ ,
同理有: ,解得 或 ,
∴P点坐标为(1, )或(1, ),对应的Q点坐标为(4, )或(4, );
情况三:AQ为菱形对角线时,另一对角线为CP ,
设P点坐标为(1,t),Q点坐标为(m , n),
同理有: ,解得 或 ,
∴P点坐标为(1, )或(1, ),对应的Q点坐标为(-2, )或(-2, );
纵上所示,Q点坐标存在,为(2,2)或(4, )或(4, )或( , )或( , ).
【分析】(1)将 , 代入二次函数表达式中,得出a、b的值,即可得到抛物线的解析式;
(2)连接BP、CP、AP,由二次函数对称性可知,BP=AP,得出 ,BC为定直线,当C、P、A三点共线时, 有最小值为 , 此时 的周长也最小,设直线AC的解析式为: , 代入 , 可得k、m的值,即可得到直线AC的解析式,二次函数的对称轴为 , 代入 , 得到 , 得到P的坐标,此时得到 的周长最小值;
(3)过点M作直线m//AC,直线m与抛物线交点即为P点,根据M的坐标可求出m的直线的表达式,联立抛物线的解析式与直线m的解析式即可求出p的坐标。
27.【答案】 (1)解:当 时,抛物线 ,
∴ (0,4),
∵点 在直线 上: 上,
∴ ,
∵直线 与 轴交点为 , ,
解得: ,
∴ (4,0),
∵点 在抛物线上,
∴ ①,
∵ ,
∴ 轴,点 、 关于抛物线对称轴对称,
∵ ,
∴抛物线对称轴为:直线 ,
∴ ②,
联立方程①②,
,
解得: ,
∴抛物线的表达式为 .
(2)解:连接 ,如图1,
∵ (0,4),点 是直线 上一动点,
∴ 、 关于直线 对称,∴ ,
∴当点 、 、 在同一直线上时, 最短,
当 时,解得: ,
∴此时, (2,2),
∵ ,
∴ ,
∴ 周长最小值为: .
(3)解:存在满足条件的点 ,
设 ( ),则 , ,
∵点 是 中点,
∴ ,
∴﹣ ,
解得: , (舍去),
∴ , , ,
①若 为菱形 边,点 在点 左侧,如图2,
延长 交 轴于点 ,
∵ , , ,
∴ °, ,
∴ ,
∴ , ,
∴ ,
②若 为菱形 边,点 在点 右侧,如图3,
∵ , , ,
∴ °, ,
∴ ,
∴ , ,
∴ ,
③若 为菱形的对角线,菱形 中,如图4,
设 与 交于点 ,
∴ , , ,
∴ 轴, ,
∴ ,
∴ ,
∴ ,
∴ .
当 、 为邻边时,
∵PM⊥MF,且PM=MF=FG=PG=3
∴四边形PMFG为正方形,
∵OM=1,
∴OF=OM+MF=1+3=4
可得 .
综上所述,满足条件的点 坐标为 或 或 或 .
【解析】【分析】(1)由抛物线过点C可求出C的坐标,由直线也经过点C即可求出n的值;得到n的值即有直线BC的关系式,即能求BC与x轴交点B的坐标,又由DE//x轴且其横坐标满足 , 即得到抛物线对称轴 , 再把点B坐标代入抛物线关系式得方程组,解得a、b的值即可;
(2)由于点Q在直线y=2上运动,要求的是OQ+BQ的最小值,O、B是定点,故寻找O或B关于直线y=2的对称点,由C(0,4)得C与O关于直线y=2对称,则有CQ=OQ,当点C、Q、B在同一直线上时有最小值,求直线BC上y=2时横坐标,即为Q的坐标,计算BC与OB的和即为三角形QOB周长最小值;
(3)先根据题意设点M、P、N坐标,利用P为MN中点的等量关系求出P、M的坐标,再对菱形四个顶点位置讨论:以PM为菱形的变,此时又分两种情况,分别是点F在点P左右侧的讨论;当F在P左侧时,根据菱形性质和GM与x轴夹角为45度易求G的坐标;当F在P右侧时,根据对称性即可求出G的坐标,以PM为菱形对角线,利用对角线互相垂直平分的性质即可求出点G坐标。
21世纪教育网(www.21cnjy.com)
同课章节目录
