浙教版初中数学八年级上册 1.3 证明(1)课件(15张PPT)
文档属性
| 名称 | 浙教版初中数学八年级上册 1.3 证明(1)课件(15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 315.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-14 00:00:00 | ||
图片预览





文档简介
(共15张PPT)
1.3 证明(1)
2、 当n=0,1,2,3,4时,代数式n2-3n+7的值分别是7,5,5,7,11,它们都是素数.那么,命题“对于自然数n,代数式n2-3n+7的值都是素数”是真命题吗
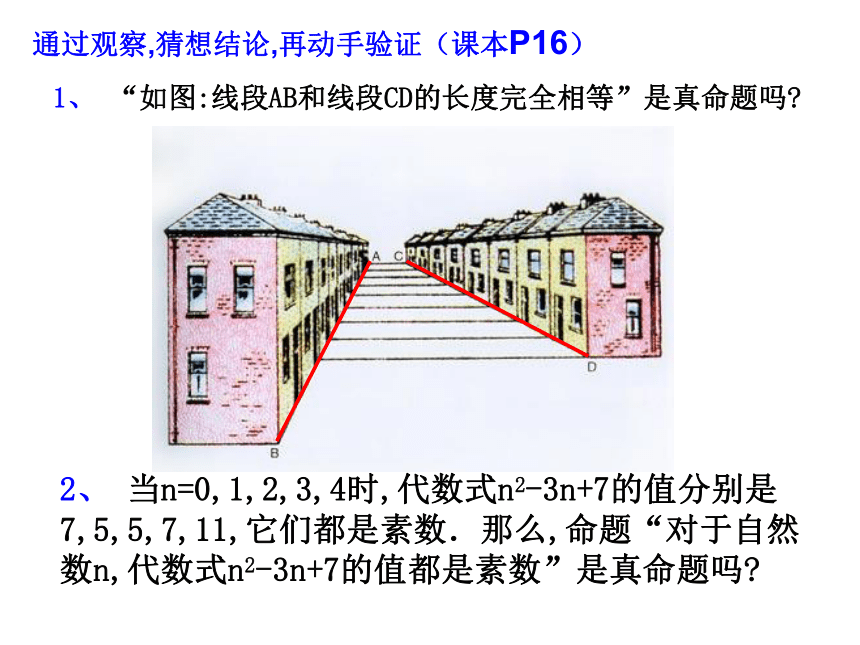
1、 “如图:线段AB和线段CD的长度完全相等”是真命题吗
通过观察,猜想结论,再动手验证(课本P16)
命题“等腰直角三角形的斜边是
直角边的 倍”是真命题吗?
请说明理由。
从命题的条件出发,根据已知的定义、公理、定理,一步一步推得结论成立,这样的推理过程叫做证明。
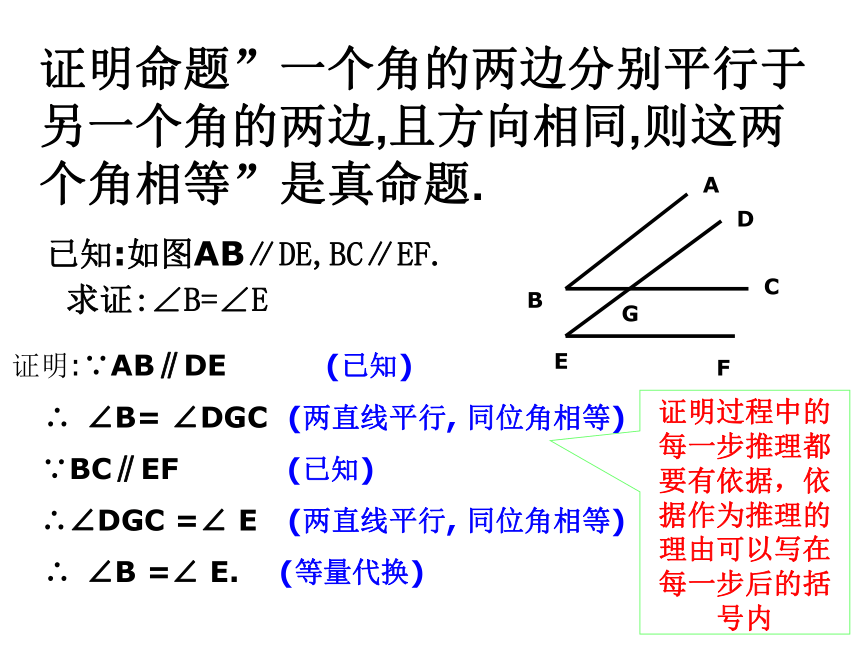
证明命题“一个角的两边分别平行于另一个角的两边,且方向相同,则这两个角相等”是真命题.
证明命题”一个角的两边分别平行于另一个角的两边,且方向相同,则这两个角相等”是真命题.
已知:如图AB∥DE,BC∥EF.
求证:∠B=∠E
证明:∵AB∥DE (已知)
∴ ∠B= ∠DGC (两直线平行, 同位角相等)
∵BC∥EF (已知)
∴∠DGC =∠ E (两直线平行, 同位角相等)
∴ ∠B =∠ E. (等量代换)
A
B
C
D
E
F
G
证明过程中的每一步推理都要有依据,依据作为推理的理由可以写在每一步后的括号内
1.根据题意,画出图形;
2.分清命题的条件和结论,结合图形,在“已知”中写出条件,在“求证”中写出结论;
3.在“证明”中写出推理过程,且每一步推理都要有依据。
证明几何命题的一般格式:
想一想:
命题“一个角的两边分别平行于另一个角的两边,且方向相同,则这两个角相等”。
思考:若把方向相同去掉会怎么样?
证明命题“两条直线被第三条所截,如果内
错角相等,那么同位角也相等”是真命题。
结论
条件
例2:已知:如图, AC与BD交于点O,
AO=CO,BO=DO .
求证:AB‖CD
A
B
C
D
O
已知:如图BC AC于点C,CD AB
于点D,∠EBC=∠A
求证:BE//CD
E
D
A
C
B
(课本P18作业题3)
本节课你有哪些收获?
小结:
1.根据题意,画出图形;
2.分清命题的条件和结论,结合图形,在“已知”中写出条件,在“求证”中写出结论;
3.在“证明”中写出推理过程。且每一步推理都要有依据。
二、证明几何命题的一般格式:
一、证明的含义
收获:
证明命题“全等三角形对应边上的高相等”
是真命题。
笑到最后才是胜利者!
结束寄语
由“因”导“果”,言必有据.是初学证明者谨记和遵循的原则.
作业:
(必做题)作业本(1)
(选做题)课本P18作业题2、4
1.3 证明(1)
2、 当n=0,1,2,3,4时,代数式n2-3n+7的值分别是7,5,5,7,11,它们都是素数.那么,命题“对于自然数n,代数式n2-3n+7的值都是素数”是真命题吗
1、 “如图:线段AB和线段CD的长度完全相等”是真命题吗
通过观察,猜想结论,再动手验证(课本P16)
命题“等腰直角三角形的斜边是
直角边的 倍”是真命题吗?
请说明理由。
从命题的条件出发,根据已知的定义、公理、定理,一步一步推得结论成立,这样的推理过程叫做证明。
证明命题“一个角的两边分别平行于另一个角的两边,且方向相同,则这两个角相等”是真命题.
证明命题”一个角的两边分别平行于另一个角的两边,且方向相同,则这两个角相等”是真命题.
已知:如图AB∥DE,BC∥EF.
求证:∠B=∠E
证明:∵AB∥DE (已知)
∴ ∠B= ∠DGC (两直线平行, 同位角相等)
∵BC∥EF (已知)
∴∠DGC =∠ E (两直线平行, 同位角相等)
∴ ∠B =∠ E. (等量代换)
A
B
C
D
E
F
G
证明过程中的每一步推理都要有依据,依据作为推理的理由可以写在每一步后的括号内
1.根据题意,画出图形;
2.分清命题的条件和结论,结合图形,在“已知”中写出条件,在“求证”中写出结论;
3.在“证明”中写出推理过程,且每一步推理都要有依据。
证明几何命题的一般格式:
想一想:
命题“一个角的两边分别平行于另一个角的两边,且方向相同,则这两个角相等”。
思考:若把方向相同去掉会怎么样?
证明命题“两条直线被第三条所截,如果内
错角相等,那么同位角也相等”是真命题。
结论
条件
例2:已知:如图, AC与BD交于点O,
AO=CO,BO=DO .
求证:AB‖CD
A
B
C
D
O
已知:如图BC AC于点C,CD AB
于点D,∠EBC=∠A
求证:BE//CD
E
D
A
C
B
(课本P18作业题3)
本节课你有哪些收获?
小结:
1.根据题意,画出图形;
2.分清命题的条件和结论,结合图形,在“已知”中写出条件,在“求证”中写出结论;
3.在“证明”中写出推理过程。且每一步推理都要有依据。
二、证明几何命题的一般格式:
一、证明的含义
收获:
证明命题“全等三角形对应边上的高相等”
是真命题。
笑到最后才是胜利者!
结束寄语
由“因”导“果”,言必有据.是初学证明者谨记和遵循的原则.
作业:
(必做题)作业本(1)
(选做题)课本P18作业题2、4
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
