浙教版初中数学八年级上册 1.3 证明(2)课件(15张PPT)
文档属性
| 名称 | 浙教版初中数学八年级上册 1.3 证明(2)课件(15张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 242.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-14 18:03:18 | ||
图片预览



文档简介
(共15张PPT)
1.3证明(2)
1.三角形三个内角的和等于多少?
2.你有哪些办法得到它?
问题1:
180°.
( 测量、拼图 )
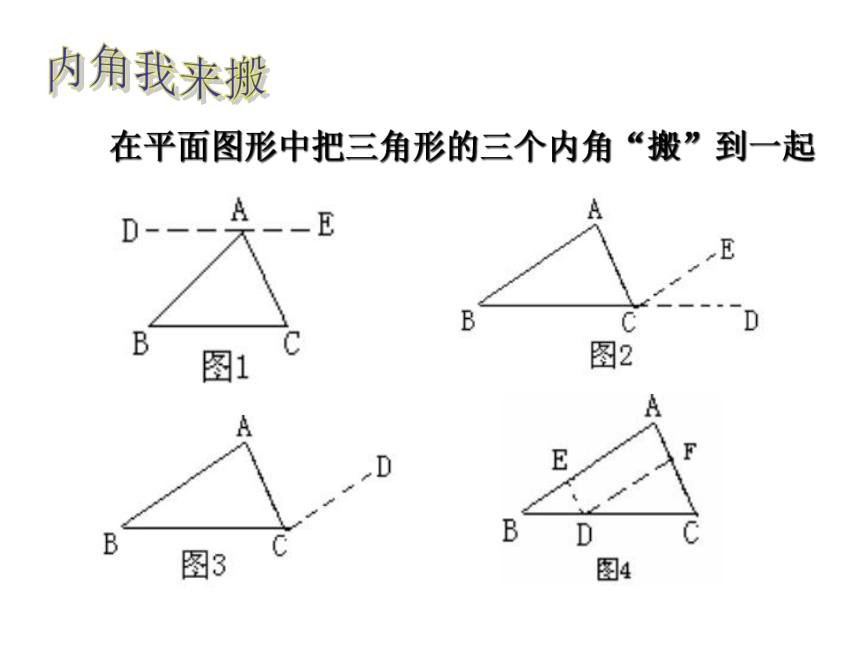
3.你什么办法在平面图形中把三角形的三个内角“搬”到一起,从而完成定理的证明?
在平面图形中把三角形的三个内角“搬”到一起
内角我来搬
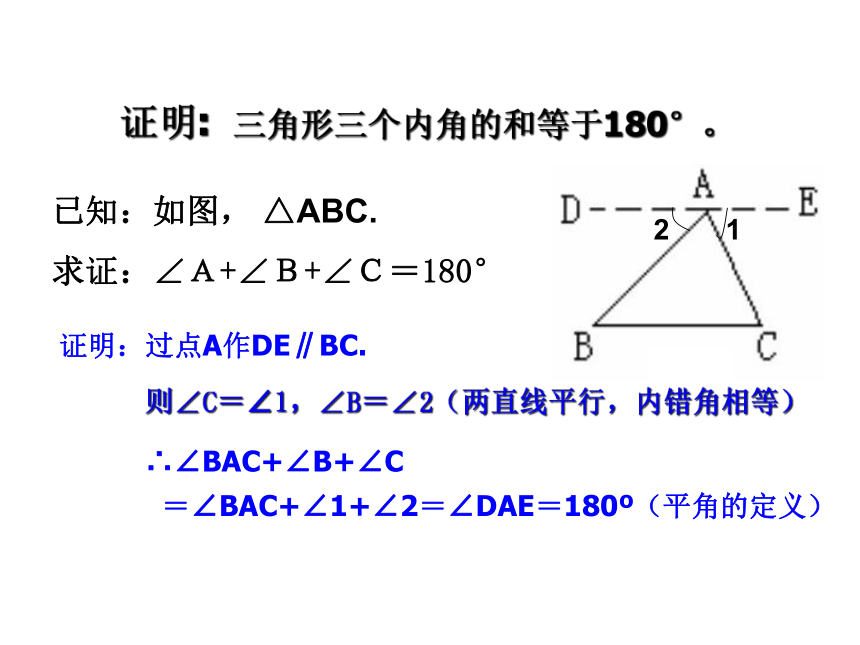
证明: 三角形三个内角的和等于180°。
已知:如图, △ABC.
求证:∠A+∠B+∠C=180°
1
2
则∠C=∠1,∠B=∠2(两直线平行,内错角相等)
证明:过点A作DE∥BC.
∴∠BAC+∠B+∠C
=∠BAC+∠1+∠2=∠DAE=180 (平角的定义)
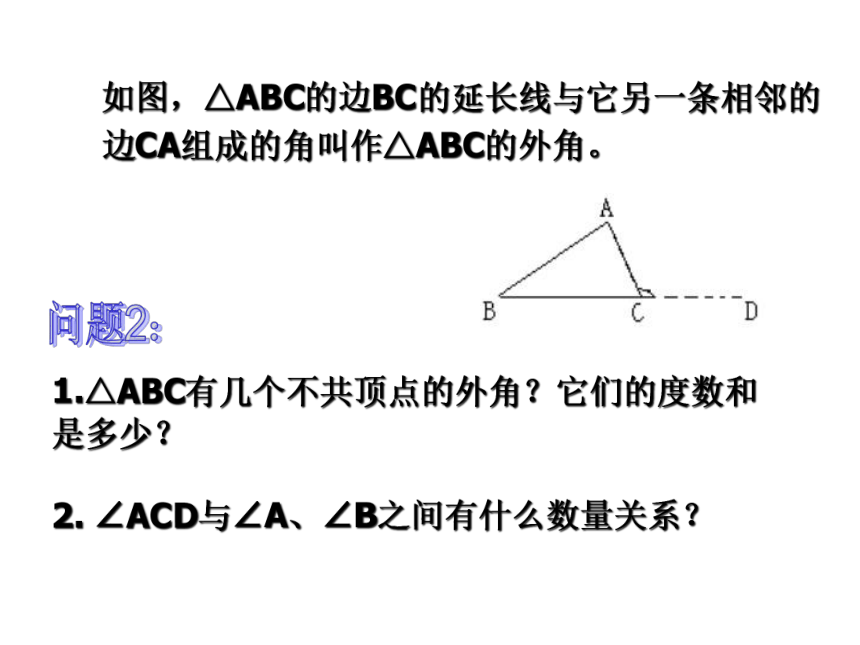
如图,△ABC的边BC的延长线与它另一条相邻的
边CA组成的角叫作△ABC的外角。
1.△ABC有几个不共顶点的外角?它们的度数和 是多少?
2. ∠ACD与∠A、∠B之间有什么数量关系?
问题2:
2.几何命题的证明格式:
归纳总结
1. 三角形三个内角的和定理;
三角形三个内角的和等于180°
根据题意,画出图形;
分清命题的条件和结论,结合图形,在“已知”中写出条件,在“求证”中写出结论;
在“证明”中写出推理过程.
归纳总结
3. 辅助线:
辅助线是为了证明需要在原图上添画的线.(通常画虚线)
作用:把分散的条件集中,把隐含的条件显现,
起到牵线搭桥的转化作用.
转化角时最常用的辅助线是添平行线。
归纳总结
4. 三角形内角和定理的2个推论:
三角形的外角等于和它不相邻的两个内角的和;
三角形的外角大于任何一个与它不相邻的内角.
几何语言:
∵∠ACD是△ABC的外角
∴ ∠ACD= ∠A+ ∠B
∵∠ACD是△ABC的外角
∴ ∠ACD>∠A
例 已知:如图,∠B+∠D=∠BCD.
求证:AB∥DE.
合作学习
例 已知:如图,∠B+∠D=∠BCD.
求证:AB∥DE.
我来晒一晒
D
A
B
C
E
E
证明:延长DC交AB于E
∵∠B+∠D= ∠BCD(已知)
∵∠BCD是△BCE 的一个外角
∴∠BCD=∠B+∠ BEC
(三角形的外角等于和它不相邻的两个内角的和)
∴ ∠B+ ∠D= ∠B+ ∠BEC
∴ ∠D= ∠ BEC
∴ AB∥DE(内错角相等, 两直线平行)
例 已知:如图,∠B+∠D=∠BCD.
求证:AB∥DE.
我来晒一晒
D
A
B
C
E
证明:连结BD
∵∠ABC+∠CDE= ∠BCD(已知)
∴ ∠ABC+ ∠CDE+∠1+ ∠2=180°
∴ AB∥DE(同旁内角互补, 两直线平行)
2
1
∠BCD+∠1+∠2=180°
(三角形的三个内角的和等于180°)
即 ∠ABD+ ∠BDE+∠C=180°
拓展提升
变式1:
上图中,若AB∥DE,则∠B+∠D=∠BCD吗?
拓展提升
变式2:
若点C的位置如图所示,且AB∥DE,
则∠B、∠D、∠BCD之间有什么数量关系?
课堂反思
今天你学到了什么?
有什么疑难和困惑吗?
1.三角形的内角和定理及推论;
2.几何命题证明的表述格式;
3.会构造“三线八角”的基本图;
4.转化的数学思想:遇截线为折线时,化折为直。
课堂反思
1.3证明(2)
1.三角形三个内角的和等于多少?
2.你有哪些办法得到它?
问题1:
180°.
( 测量、拼图 )
3.你什么办法在平面图形中把三角形的三个内角“搬”到一起,从而完成定理的证明?
在平面图形中把三角形的三个内角“搬”到一起
内角我来搬
证明: 三角形三个内角的和等于180°。
已知:如图, △ABC.
求证:∠A+∠B+∠C=180°
1
2
则∠C=∠1,∠B=∠2(两直线平行,内错角相等)
证明:过点A作DE∥BC.
∴∠BAC+∠B+∠C
=∠BAC+∠1+∠2=∠DAE=180 (平角的定义)
如图,△ABC的边BC的延长线与它另一条相邻的
边CA组成的角叫作△ABC的外角。
1.△ABC有几个不共顶点的外角?它们的度数和 是多少?
2. ∠ACD与∠A、∠B之间有什么数量关系?
问题2:
2.几何命题的证明格式:
归纳总结
1. 三角形三个内角的和定理;
三角形三个内角的和等于180°
根据题意,画出图形;
分清命题的条件和结论,结合图形,在“已知”中写出条件,在“求证”中写出结论;
在“证明”中写出推理过程.
归纳总结
3. 辅助线:
辅助线是为了证明需要在原图上添画的线.(通常画虚线)
作用:把分散的条件集中,把隐含的条件显现,
起到牵线搭桥的转化作用.
转化角时最常用的辅助线是添平行线。
归纳总结
4. 三角形内角和定理的2个推论:
三角形的外角等于和它不相邻的两个内角的和;
三角形的外角大于任何一个与它不相邻的内角.
几何语言:
∵∠ACD是△ABC的外角
∴ ∠ACD= ∠A+ ∠B
∵∠ACD是△ABC的外角
∴ ∠ACD>∠A
例 已知:如图,∠B+∠D=∠BCD.
求证:AB∥DE.
合作学习
例 已知:如图,∠B+∠D=∠BCD.
求证:AB∥DE.
我来晒一晒
D
A
B
C
E
E
证明:延长DC交AB于E
∵∠B+∠D= ∠BCD(已知)
∵∠BCD是△BCE 的一个外角
∴∠BCD=∠B+∠ BEC
(三角形的外角等于和它不相邻的两个内角的和)
∴ ∠B+ ∠D= ∠B+ ∠BEC
∴ ∠D= ∠ BEC
∴ AB∥DE(内错角相等, 两直线平行)
例 已知:如图,∠B+∠D=∠BCD.
求证:AB∥DE.
我来晒一晒
D
A
B
C
E
证明:连结BD
∵∠ABC+∠CDE= ∠BCD(已知)
∴ ∠ABC+ ∠CDE+∠1+ ∠2=180°
∴ AB∥DE(同旁内角互补, 两直线平行)
2
1
∠BCD+∠1+∠2=180°
(三角形的三个内角的和等于180°)
即 ∠ABD+ ∠BDE+∠C=180°
拓展提升
变式1:
上图中,若AB∥DE,则∠B+∠D=∠BCD吗?
拓展提升
变式2:
若点C的位置如图所示,且AB∥DE,
则∠B、∠D、∠BCD之间有什么数量关系?
课堂反思
今天你学到了什么?
有什么疑难和困惑吗?
1.三角形的内角和定理及推论;
2.几何命题证明的表述格式;
3.会构造“三线八角”的基本图;
4.转化的数学思想:遇截线为折线时,化折为直。
课堂反思
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
