第一章反比例函数复习教案
图片预览

文档简介
反比例函数(复习)
复习目标:
1、通过知识点与相应题目相结合,进一步巩固本章知识点;
2、选取近几年关于本章知识相应中考题,让学生在学习时有的放矢。
3、本章内容对学生来说有点难度,复习时把握难易度,通过师生对话,
降少学生的恐惧感。
复习重点:(1)反比例函数的概念;
(2)反比例函数的图象和性质;
(3)利用反比例函数图象的性质解决实际应用问题。
复习难点:利用反比例函数图象的性质解决实际应用问题。
教学过程:
一、知识回顾
1、什么是反比例函数?
一般地,形如 ( k是常数, k = 0 ) 的函数叫做反比例函数。
注意:(1)常数 k 称为比例系数,k 是非零常数;
(2)自变量 x 次数不是 1; x 与 y 的积是非零常数, 即 xy = k,k = 0;
(3)解析式有二种常见的表达形式。和()
例1、(1)下列函数,① ②. ③ ④.⑤
⑥ ;其中是y关于x的反比例函数的有:_________________。
(2)如果是的反比例函数,是的反比例函数,那么是的( )
A.反比例函数 B.正比例函数 C.一次函数 D.反比例或正比例函数
(3)反比例函数的图象经过(—2,5)和(, ),
求(1)的值;(2)判断点B(,)是否在这个函数图象上,并说明理由。
(4)已知函数,其中与成正比例, 与成反比例,且当=1时,
=1;=3时,=5.求:(1)求关于的函数解析式;(2)当=2时,的值.
2、你能回顾与总结反比例函数的图象性质与特征吗?(师提问,学生个别作答)
形 状 图象是双曲线
位 置 当k>0时,双曲线分别位于第一,三象限内当k<0时, 双曲线分别位于第二,四象限内
增减性 当k>0时,在每一象限内,y随x的增大而减小当k<0时,在每一象限内,y随x的增大而增大
变化趋势 双曲线无限接近于x、y轴,但永远不会与坐标轴相交
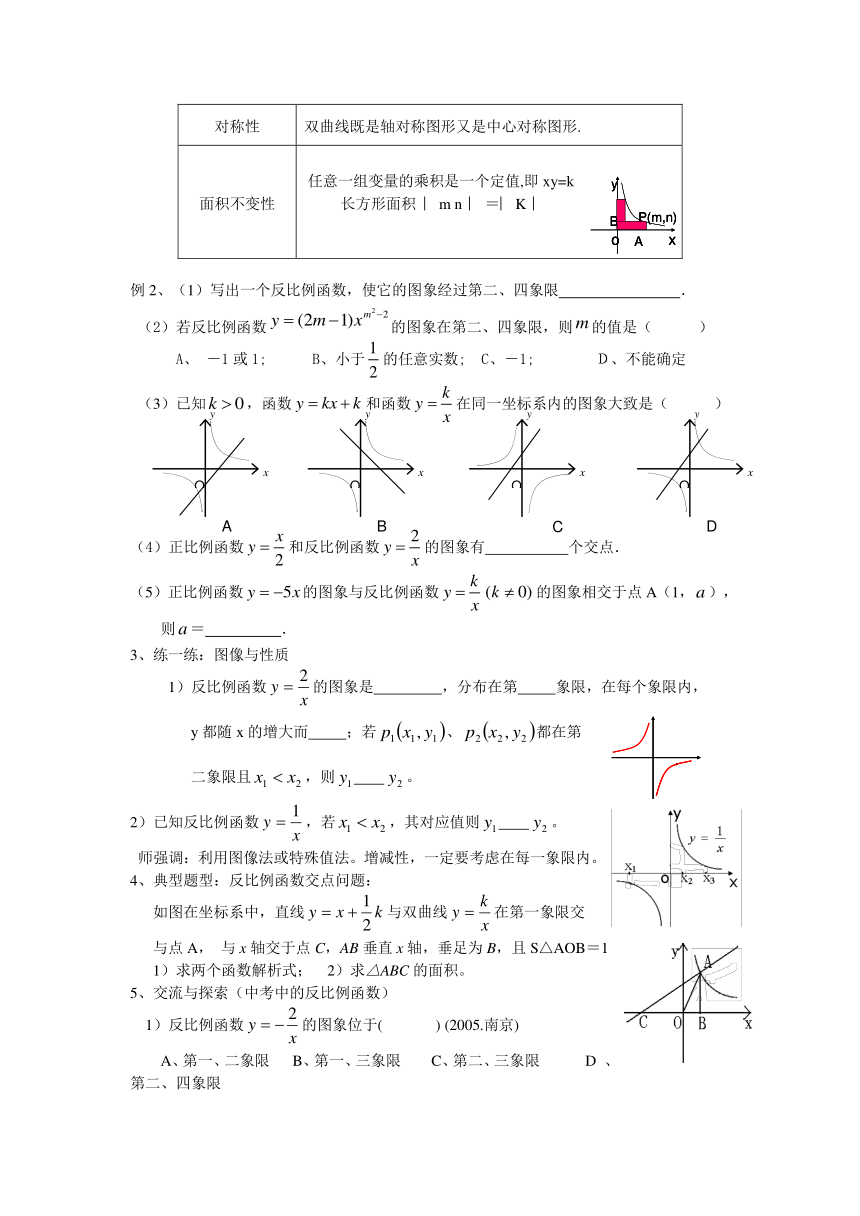
对称性 双曲线既是轴对称图形又是中心对称图形.
面积不变性 任意一组变量的乘积是一个定值,即xy=k长方形面积 ︳m n︱ =︳K︱
例2、(1)写出一个反比例函数,使它的图象经过第二、四象限 .
(2)若反比例函数的图象在第二、四象限,则的值是( )
A、 -1或1; B、小于的任意实数; C、-1; D、不能确定
(3)已知,函数和函数在同一坐标系内的图象大致是( )
(4)正比例函数和反比例函数的图象有 个交点.
(5)正比例函数的图象与反比例函数的图象相交于点A(1,),
则= .
3、练一练:图像与性质
1)反比例函数的图象是 ,分布在第 象限,在每个象限内,
y都随x的增大而 ;若、都在第
二象限且,则 。
2)已知反比例函数,若,其对应值则 。
师强调:利用图像法或特殊值法。增减性,一定要考虑在每一象限内。
4、典型题型:反比例函数交点问题:
如图在坐标系中,直线与双曲线在第一象限交
与点A, 与x轴交于点C,AB垂直x轴,垂足为B,且S△AOB=1
1)求两个函数解析式; 2)求△ABC的面积。
5、交流与探索(中考中的反比例函数)
1)反比例函数的图象位于( ) (2005.南京)
A、第一、二象限 B、第一、三象限 C、第二、三象限 D 、第二、四象限
2)若反比例函数 经过点A(m,-2m),则m的值为( ) (2005.陕西)
A、 B、3 C、 D、±3
3)函数 的图象经过(2,-2),则此函数的图象在平面直角坐标系中的( ) (2005.深圳) A、第一、三象限 B、第三、四象限
C、第一、二象限 D、第二、四象限
4)反比例函数的图象经过点(2,5),若点(1, n)在反比例函数的图象上,则n等于( ) (2005.福州)
A、10 B、5 C、2 D、
5)(2005.桂林)已知反比例函数 的图象在第一、三象限,那么 m的取值范围是__________ 。
6)如果反比例函数的图象经过点(1,-2),那么这个反比例函数的解析式__。 (2005.北京)
7)已知甲,乙两地相距s km,汽车从甲地匀速行驶到乙地.如果汽车每小时耗油量为a L,那么从甲地到乙地的总耗油量y (L)与汽车的行驶速度v (km/h)的函数图象大致是( ). (2005.江西)
8)你吃过拉面吗?实际上在做拉面的过程中就渗透着数学知识:一定体积的面团做成拉面,面条的总长度y (m)是面条的粗细(橫截面积)s()的反比例函数,其图象如图所示。
(1)写出y与s的函数关系式; (2)求当面条粗1.6㎜2时,面条的总长度是多少?
9)已知反比例函数的图象经过点,若一次函数的图象平移后经过该反比例函数图象上的点B(2,m),求平移后的一次函数的图象与x轴的交点坐标。 (2005.北京海淀)
思路分析:本题综合考查反比例函数、一次函数及平移等知识,解题的关键是确定反比例函数的关系式。
二 巧用图象
比较大小
设计意图:巩固比较大小的方法,利用函数的增减性,判断符号,利用图象等方法,特别是利用函数图象这样方法非常直观,快速,准确,很值得同学们去掌握。
归纳数学思想方法:数形结合思想
有关方程组,不等式问题
设计意图:通过两个函数图象解决有关方程组,不等式的问题,特别是第6题,学生不会或者解不完整这样的不等式,这里就给大家提供了一种非常巧妙地方法。
3.有关面积的问题
设计意图:从三角形AOE的面积为反比例系数一半的绝对值出发,利用等底等高两个三角形面积相等这些性质需要三角形,四边形面积之间的关系,从而让学生的思维有一个提升。
课堂小结:
O
O
O
O
B
A
D
C
o
(A) (B) (C) (D)
V(km/h)
Y/L
o
V(km/h)
Y/L
o
V(km/h)
Y/L
o
V(km/h)
Y/L
复习目标:
1、通过知识点与相应题目相结合,进一步巩固本章知识点;
2、选取近几年关于本章知识相应中考题,让学生在学习时有的放矢。
3、本章内容对学生来说有点难度,复习时把握难易度,通过师生对话,
降少学生的恐惧感。
复习重点:(1)反比例函数的概念;
(2)反比例函数的图象和性质;
(3)利用反比例函数图象的性质解决实际应用问题。
复习难点:利用反比例函数图象的性质解决实际应用问题。
教学过程:
一、知识回顾
1、什么是反比例函数?
一般地,形如 ( k是常数, k = 0 ) 的函数叫做反比例函数。
注意:(1)常数 k 称为比例系数,k 是非零常数;
(2)自变量 x 次数不是 1; x 与 y 的积是非零常数, 即 xy = k,k = 0;
(3)解析式有二种常见的表达形式。和()
例1、(1)下列函数,① ②. ③ ④.⑤
⑥ ;其中是y关于x的反比例函数的有:_________________。
(2)如果是的反比例函数,是的反比例函数,那么是的( )
A.反比例函数 B.正比例函数 C.一次函数 D.反比例或正比例函数
(3)反比例函数的图象经过(—2,5)和(, ),
求(1)的值;(2)判断点B(,)是否在这个函数图象上,并说明理由。
(4)已知函数,其中与成正比例, 与成反比例,且当=1时,
=1;=3时,=5.求:(1)求关于的函数解析式;(2)当=2时,的值.
2、你能回顾与总结反比例函数的图象性质与特征吗?(师提问,学生个别作答)
形 状 图象是双曲线
位 置 当k>0时,双曲线分别位于第一,三象限内当k<0时, 双曲线分别位于第二,四象限内
增减性 当k>0时,在每一象限内,y随x的增大而减小当k<0时,在每一象限内,y随x的增大而增大
变化趋势 双曲线无限接近于x、y轴,但永远不会与坐标轴相交
对称性 双曲线既是轴对称图形又是中心对称图形.
面积不变性 任意一组变量的乘积是一个定值,即xy=k长方形面积 ︳m n︱ =︳K︱
例2、(1)写出一个反比例函数,使它的图象经过第二、四象限 .
(2)若反比例函数的图象在第二、四象限,则的值是( )
A、 -1或1; B、小于的任意实数; C、-1; D、不能确定
(3)已知,函数和函数在同一坐标系内的图象大致是( )
(4)正比例函数和反比例函数的图象有 个交点.
(5)正比例函数的图象与反比例函数的图象相交于点A(1,),
则= .
3、练一练:图像与性质
1)反比例函数的图象是 ,分布在第 象限,在每个象限内,
y都随x的增大而 ;若、都在第
二象限且,则 。
2)已知反比例函数,若,其对应值则 。
师强调:利用图像法或特殊值法。增减性,一定要考虑在每一象限内。
4、典型题型:反比例函数交点问题:
如图在坐标系中,直线与双曲线在第一象限交
与点A, 与x轴交于点C,AB垂直x轴,垂足为B,且S△AOB=1
1)求两个函数解析式; 2)求△ABC的面积。
5、交流与探索(中考中的反比例函数)
1)反比例函数的图象位于( ) (2005.南京)
A、第一、二象限 B、第一、三象限 C、第二、三象限 D 、第二、四象限
2)若反比例函数 经过点A(m,-2m),则m的值为( ) (2005.陕西)
A、 B、3 C、 D、±3
3)函数 的图象经过(2,-2),则此函数的图象在平面直角坐标系中的( ) (2005.深圳) A、第一、三象限 B、第三、四象限
C、第一、二象限 D、第二、四象限
4)反比例函数的图象经过点(2,5),若点(1, n)在反比例函数的图象上,则n等于( ) (2005.福州)
A、10 B、5 C、2 D、
5)(2005.桂林)已知反比例函数 的图象在第一、三象限,那么 m的取值范围是__________ 。
6)如果反比例函数的图象经过点(1,-2),那么这个反比例函数的解析式__。 (2005.北京)
7)已知甲,乙两地相距s km,汽车从甲地匀速行驶到乙地.如果汽车每小时耗油量为a L,那么从甲地到乙地的总耗油量y (L)与汽车的行驶速度v (km/h)的函数图象大致是( ). (2005.江西)
8)你吃过拉面吗?实际上在做拉面的过程中就渗透着数学知识:一定体积的面团做成拉面,面条的总长度y (m)是面条的粗细(橫截面积)s()的反比例函数,其图象如图所示。
(1)写出y与s的函数关系式; (2)求当面条粗1.6㎜2时,面条的总长度是多少?
9)已知反比例函数的图象经过点,若一次函数的图象平移后经过该反比例函数图象上的点B(2,m),求平移后的一次函数的图象与x轴的交点坐标。 (2005.北京海淀)
思路分析:本题综合考查反比例函数、一次函数及平移等知识,解题的关键是确定反比例函数的关系式。
二 巧用图象
比较大小
设计意图:巩固比较大小的方法,利用函数的增减性,判断符号,利用图象等方法,特别是利用函数图象这样方法非常直观,快速,准确,很值得同学们去掌握。
归纳数学思想方法:数形结合思想
有关方程组,不等式问题
设计意图:通过两个函数图象解决有关方程组,不等式的问题,特别是第6题,学生不会或者解不完整这样的不等式,这里就给大家提供了一种非常巧妙地方法。
3.有关面积的问题
设计意图:从三角形AOE的面积为反比例系数一半的绝对值出发,利用等底等高两个三角形面积相等这些性质需要三角形,四边形面积之间的关系,从而让学生的思维有一个提升。
课堂小结:
O
O
O
O
B
A
D
C
o
(A) (B) (C) (D)
V(km/h)
Y/L
o
V(km/h)
Y/L
o
V(km/h)
Y/L
o
V(km/h)
Y/L
同课章节目录
