有理数的乘方（2）[上学期]

课件20张PPT。3/16/2019哪里有数，哪里就有美1有理数的乘方（2）浙江衢州华茂外国语学校余金耀3/16/2019哪里有数，哪里就有美2复 习填空：2、式子 表示的意义是_________。1、 在 中，a叫做____，n叫做____，
乘方的结果叫做____。底数指数幂n个a相乘3. (-4)8 __ 0 (-4)9__ 0><3/16/2019哪里有数，哪里就有美3 试一试:用三个2组成
一个最大的数.=41943043/16/2019哪里有数，哪里就有美4想一想（1） 和 有什么不同？ 说明：主要从以下几个方面考虑：
①底数
②指数
③读法
④意义
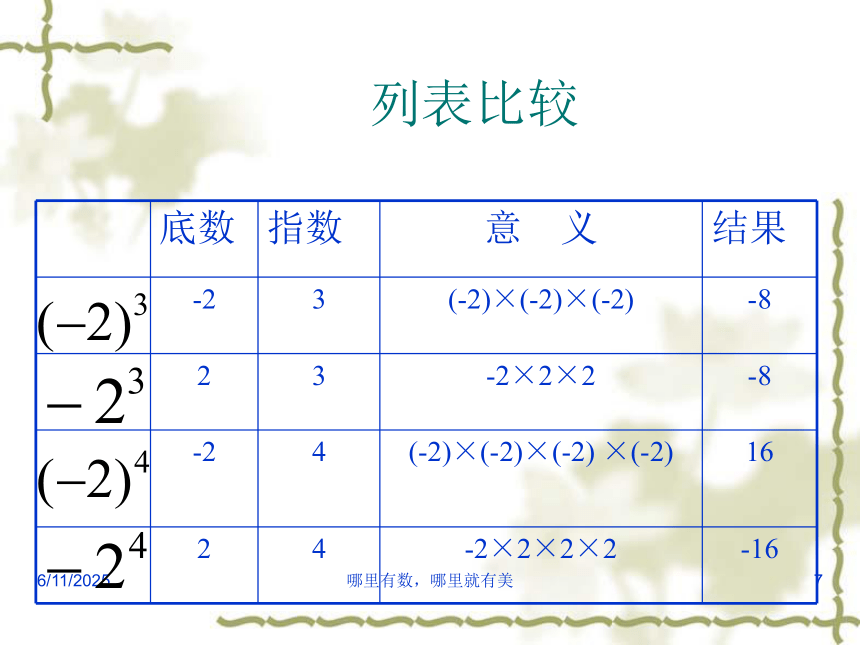
⑤结果3/16/2019哪里有数，哪里就有美5想一想（2） 和 的有什
么不同？运算结果是否相同？（3）(-2)4 和 -24 呢？3/16/2019哪里有数，哪里就有美6列表比较3/16/2019哪里有数，哪里就有美7列表比较3/16/2019哪里有数，哪里就有美8练一练 计算：3/16/2019哪里有数，哪里就有美9练一练计算：3/16/2019哪里有数，哪里就有美101. 2003年10月15日,中国首次进行载人航天飞行,飞船绕地球飞行14圈,行程约60万km，已知赤道长度约40000km，飞船行程相当于多少个赤道长？3/16/2019哪里有数，哪里就有美11数太大，读写不方便，怎么办？13000000×0.5=6500000(kg)2. 如果某市每人每天节约用水0.5kg，该市约有1千3百万人口，那么该市每天节约用水多少kg？3/16/2019哪里有数，哪里就有美121．计算： 102=（ ），103=（ ），
104=（ ），105=（ ），…… 100100010000100000得出结论： 指数为2，幂的最末有2个零，指数为3，幂的最末有3个零，指数为4，幂的最末有4个零，指数为5，幂的最末有5个零，一般地指数为n，幂的最末有n个零，反之亦然。2. 1000 000=（ ） 100 000 000 000=（ ）20 000=（ ）10610112×1043/16/2019哪里有数，哪里就有美13 我们经常遇到一些较大的数，为了使较大的数读写方便，我们常常用10的乘方来表示， 例如：600000=6×100000=6×105，
20000000=2×10000000=2×107，
570000000=5.7×100000000=5.7×108 把一个数表示成a（1≤a＜10，即带一位整数的数）与10的幂相乘形式，叫做科学记数法。 定义:第一因数是带一位整数的小数，第二个因数的指数比原数的位数小1。 注意!!!3/16/2019哪里有数，哪里就有美14请你抉择：3570000用科学记数法表示应选（ ）A 35.7×104 B 35.7 ×105
C 357 ×104 D 3.57 ×106其他选项为什么错？当个小老师！D3/16/2019哪里有数，哪里就有美15（2）下列用科学记数法表示的数，原来各是什么数？
4.315×103； 1.02×106； 解: (2) 4.315×103=4315； 1.02×106=1020000； 3/16/2019哪里有数，哪里就有美16 如果平均每人每天需要粮食0.5kg，那么全国每天大约需要粮食多少kg？1年呢？（全国人口约1.3×109人，结果用科学记数法表示）？ 解:全国每天大约需要粮食0.5×1.3×109= 0.65×109
=6.5×109÷10=6.5×108(kg)
1年大约需要粮食6.5×108×365=237250000000
=2.3725×1011(kg) 注意：解题时首先要列式，然后根据题目的要求把运算结果
用科学记数法表示。 3/16/2019哪里有数，哪里就有美17要认真呀！巩固练习1．完成课内练习1，2
2．完成课本中的探究活动 3/16/2019哪里有数，哪里就有美181．遇到较大的数时可用科学记数法来表示？3．用科学记数法a×10n表示大数关键要注意两点：
(１)１≤a＜10．
(２)当大数是大于10的整数时,n为整数位数减去１.2．用科学记数法表示大数有什么好处？本节课你有什么收获？一般形式： a×10n（ １≤a＜10，n为正整数）3/16/2019哪里有数，哪里就有美19试一试：设n为正整数，计算：
(1) (-1)2n
(2) (-1)2n+13/16/2019哪里有数，哪里就有美20再见！