准确数和近似数的说课稿[上学期]

课件31张PPT。义务教育课程标准实验教科书《数字》　　
七年级上册
　2.7准确数和近似数
　　　说课稿
　　　　《2.7准确数和近似数》说课教学准备教学手段教法指导教学设计教材分析学法指导一.教材分析
1.教材的地位和作用《2.7准确数和近似数》说课一.教材分析
1.教材的地位和作用2.教学目标①通过实例让学生经历近似数和准确数概念的产生过程。
②了解近似数的精确度的两种表示方式。
③能说出由四舍五入得到的有理数的精确位数和有效数字。
④会根据预定精确度取近似值并体验这种过程。《2.7准确数和近似数》说课教学难点：有效数字的概念。3.教学重点和难点
教学重点：近似数的两种表示方式，及近似值的取法。 《2.7准确数和近似数》说课二 .教学准备：
　印足够数量的表格分发给每个合作小组《2.7准确数和近似数》说课三.　教学手段：多媒体辅助教学《2.7准确数和近似数》说课四.　教法指导：
　　采用小组讨论的形式，以学生自主探究与合作，教师组织、引导的方式进行，并配以适当的练习加以巩固。《2.7准确数和近似数》说课《2.7准确数和近似数》说课五．学法指导
学生及合作小组通过动手、动口、动脑等活动，主动探索、发现问题；互动合作，解决问题；归纳概括，形成能力。恰如其分的问题设计，让学生亲历探究，突出学生教学主体的地位。《2.7准确数和近似数》说课六．教学设计
（1）整体设计　　理论依据：
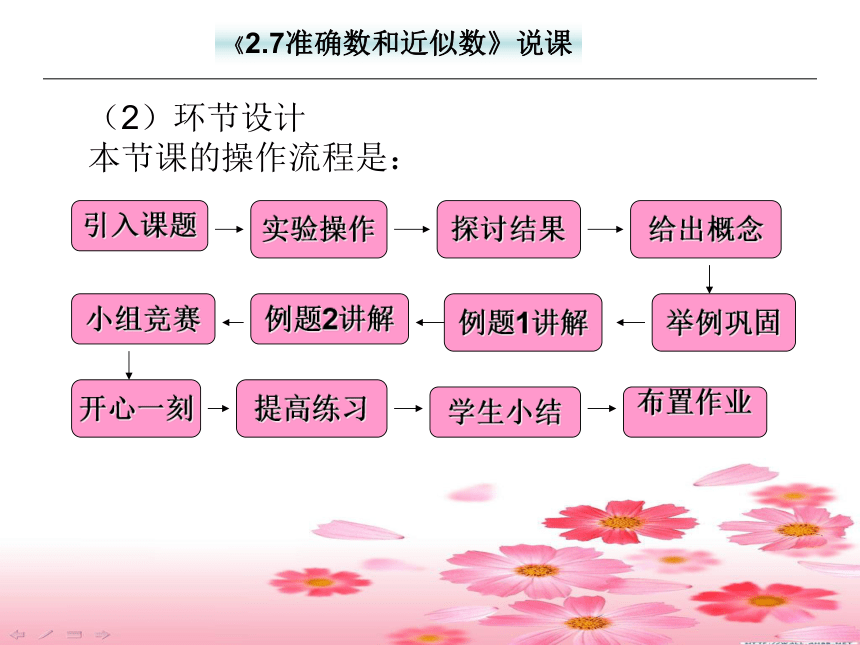
“发现问题――提出问题――解决问题――回顾” 　经验和自然相互联系（2）环节设计
本节课的操作流程是：《2.7准确数和近似数》说课引入课题布置作业
学生小结提高练习开心一刻小组竞赛例题2讲解例题1讲解举例巩固给出概念探讨结果实验操作北京某高科技蔬菜园区通过高新技术，培育出20株高产番茄树，其中最大的一株高达2米，树冠枝条面积达25平方米，结有番茄15000个左右。合作学习每组抽一个课题统计，并填好表格：
（1）班上男女生人数；　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（2）全年级人数；　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（3）同学们用的数学课本的厚度；　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（4）中国人口数量；　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（5）圆周率。　　 教师巧设提问，步步引导！一.定义：
　与实际完全符合的数称为准确数
　与实际接近的数称为近似数你能举例说出一些日常生活中常见的近数
　　　　和准确数的例子 吗？你一言我一语例1　下列由四舍五入法得到的近似数各精确到哪一位？
　　　各有几个有效数字？
（1）11亿　　（2）36.8　　（3）1.2万　　（4）1.20万例2　用四舍五入法，按括号内的要求对下列各数取近似值：
（1）0.33448（精确到千分位）
（2）64.8（精确到个位）
（3）1.5952（精确到0.01）
（4）0.05069（保留2个有效数字）
（5）84960（保留3个有效数字）近似数的两种取法：　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
※　精确到哪一位或是精确到0.1，0.01等。　　　　　　　　　　　　　　　　　　　　　　　　　
※　有效数字去尾法　　如1.25用去尾法精确到0.1，则表示为1.2
进一法　　如1.23用进一法精确到0.1，则表示为1.31.选择题：
（1）下列表述中，用到准确数的是（　　）
（A）王敏的钢笔长14.5cm。 （B）一只苹果的质量是200克。
（C）七年级一班有学生48人.（D）据第五次人口普查，我国
　　　　　　　　　　　　　　 的人口总数为1295330000人。（2）把0.70945四舍五入到千分位是（　　）
（A）0.709　　 （B）0.710　 （C）0.71　 （D） 0.7095。（3）把200098000四舍五入，保留四个有效数字的近似
　　 数是（　 ）
（A） 2000　（B） 2001　（C） 2000×104（D 2.001×108 3.对表中各数按要求取近似值：
2.近似数10.50精确到＿＿＿位，有＿＿＿个有效数字。 4.由四舍五入得到的近似数83.50，精确到___位，它表示大于或等于____，而小于____的数。
　　5.世界上最深的海沟是太平洋的马里亚那海沟，海拔高度为-11034m。请按要求分别取这个数的近似数，并回答下面的问题：
（1）精确到十位，该近似数有几个有效数字？
（2）保留2个有效数字，该近似数精确到哪一位？
　6.小明和小红分别测量了同一片树叶的长度，小明读出的数据为6.8cm，小红读出的数据为6.80cm，谁的测量结果会更精确些呢？请说明理由。 历史课上，王老师讲到：“我们中华民族有着五千年悠久的历史……” 小A突然举手“老师，你说错了，早在三年前我的小学老师就告诉我们中华民族有着五千年的历史，那么到现在应该有5003年的历史了！”2. 解下列各题（请按实际意义取近似值）：
???? ??(1)全班51人都参加100米跑测验，最多6人一组，问至
　 少成 几组？
?????? (2)每辆汽车需装4只轮胎，51只轮胎能装配成几辆汽车？
1.中国的国土面积约为9596960千米2，美国和罗马尼亚
的国土面积分别约为9364000千米2（四舍五入到千位）
和240000千米2（四舍五入到万位）。如果要将中国国
土面积与它们相比较，那么中国国土面积分别四舍五
入至哪一位时，比较起来的误差可能会小一些？ 谁能说出一些日常生活中常见的近似数和准确数的例子？” “教室有44张桌子，44张椅子，4扇窗户，这些是准确数。” “我的身高是1.61米，今年12岁，这些是近似数。” “我们学校有1000多人，这是近似数。” “我们学校有1000多人，与实际相差太远，这不是近似数。” “初一（5）班约有40人，教室大概有10盏灯为近似数？” 今天有哪些收获？配套作业本
　　　　每个小组整理一篇报告，
　　要求：在报告中包括5个准确数和10个近似数，近似数中有5个要求保留5种不同要要求的有效数字，另5个精确到某一位，也是5种不同的精确度要求。并在报告中的数据上增加脚注，说明是准确数或近似数，是近似数的是用什么方法取得近似值。 我喜爱的数据新闻发布会　　　　　　板书设计
一．定义：　　　　　　　　　　　　　　　　
准确数：与实际完全符合的数称为准确数　
近似数：与实际接近的数称为近似数
二．近似数的两种取法：　　　　　　
※ 精确到哪一位或是精确到0.1，0.01等。　　　　　　　　　　　　　　　　　　　
※　保留几个有效数字
去尾法　如1.25用去尾法精确到0.1，则表示为1.2
进一法　如1.23用进一法精确到0.1，则表示为1.3
　　 第一版块　　　　　　　　　　板书设计
三。注意事项：
　☆。无论是近似数还是准确数，它首先是一个具体的
　　　数。诸如1000多、不到1000等，均不能称之为近似数。
　。近似数1.2万精确到千位，不是十分位，单位万不可忽略。
　。近似数1.2万有2个有效数字。
　　1.2万＝12000，就以为是5个不效数字，这是错误的。　
例1．　解：
　　　　　　　　　　第二版块 谢谢！