3.2 实数[上学期]

课件18张PPT。3.2 实 数是非题:
16的平方根是42（ ）
16的算术平方根是4 （ ）
-4是16的平方根（ ）
16的平方根是4与-4 （ ）
平方根等于本身的数1,0 （ ）
算术平方根等于本身的数是1 （ ）
-1的平方根是+1与-1 （ ）
3的算术平方根记作3= （ ）求下列各数的平方根与算术平方根
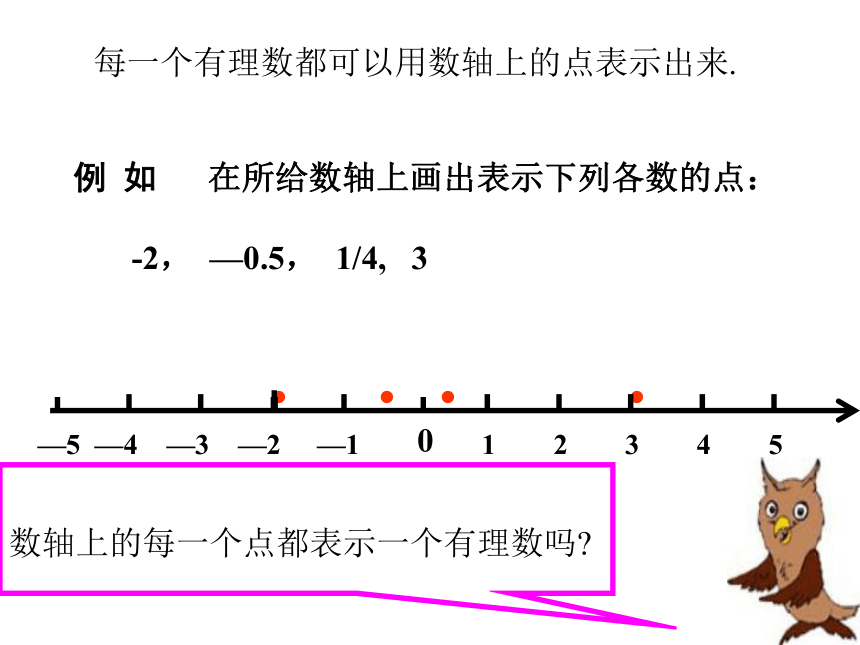
0, 9, 81, 7, 0.36, 0.0001, ,2500填空:(2)估计 的值在哪两个整数之间?探究活动例 如 在所给数轴上画出表示下列各数的点：
-2， —0.5， 1/4, 3 ····0 —3 —2 —1 1 2 3 4 5—5 —4每一个有理数都可以用数轴上的点表示出来.
数轴上的每一个点都表示一个有理数吗?
是介于1和2之间的一个数，请在表中的空白处填上适当的不等号. 合作学习： < < < < < < < < < < < < < < < < < < < <像 这种无限不循环小数叫做无理数无理数广泛存在着，无理数一般有三种情况：
①如 等，但 等是有理数；③1.010010001…（两个1之间依次多一个0），
95.6868868886…（两个6之间依次多一个8）等.② 等；实数有理数无理数正有理数零负有理数正无理数负无理数有理数和无理数统称实数．（无限不循环小数）(有限小数或无限循环小数）1）在 中，属于有理数的：
属于无理数的：
属于实数的有：2） 的相反数是 ， 的相反数是3）4）一个数的绝对值是π，则这个数是 例：把下列实数表示在数轴上，并比较它们的
大小（用“<”号连接）解：在数轴上表示如下。由上图得，－ <－1.4< <1.5<π<3.3 -2 -1 0 1 2 3 4 5····1.53.3··-1.4想一想：
　判断下列说法是否正确，并举例说明理由。
　　①两个无理数的和一定是无理数；
　　②两个无理数的积一定是无理数；
-2 -1 0 1 2 3 4 5试一试：
你能在数轴上表示出 吗？归纳总结谈一谈：本节课你有何收获？布置作业1、必做题：课本第67页A组、B组题。
2、选做题：课本第67页C组题。
3、 作业题:p14谢谢!用“ < ”“ > ”号，或数字填空：想一想
(1) 1.732____( )2_____1.742
1.73_____ ____1.74,
______ (结果保留2个有效数字);
2.4492_____( )2_____2.4502,
2.449_____( )_______2.450,
______ (结果保留3个有效数字) < < < < < < < <2.451.7