浙教版八年级上册2.1 图形的轴对称课件(共21张PPT)
文档属性
| 名称 | 浙教版八年级上册2.1 图形的轴对称课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-23 00:00:00 | ||
图片预览






文档简介
(共21张PPT)
2.1图形的轴对称
2.1轴对称图形
问题情境:
A
B
(1)
(2)
将线段AB沿它的垂直平分线折起来,那么直线两旁的部分会重合吗?
A
O
B
将∠AOB沿它的平分线所在的直线折起来,那么直线两旁的部分会重合吗?
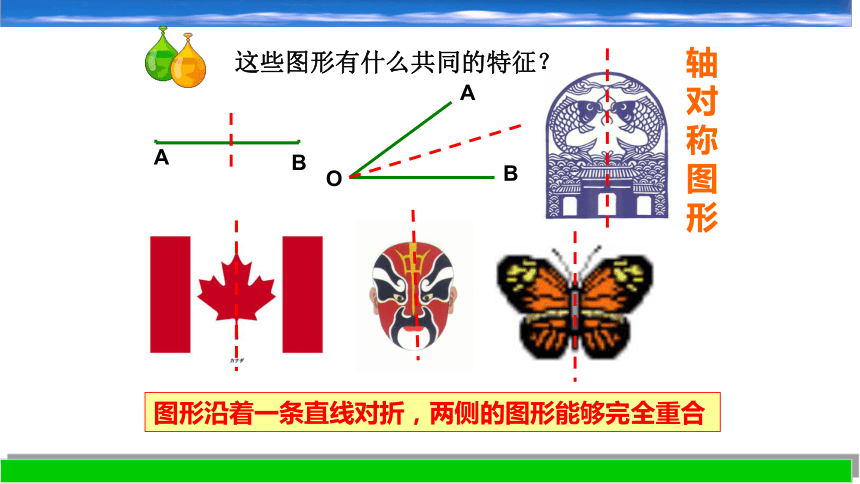
这些图形有什么共同的特征?
图形沿着一条直线对折,两侧的图形能够完全重合
轴
对
称
图
形
A
B
A
O
B
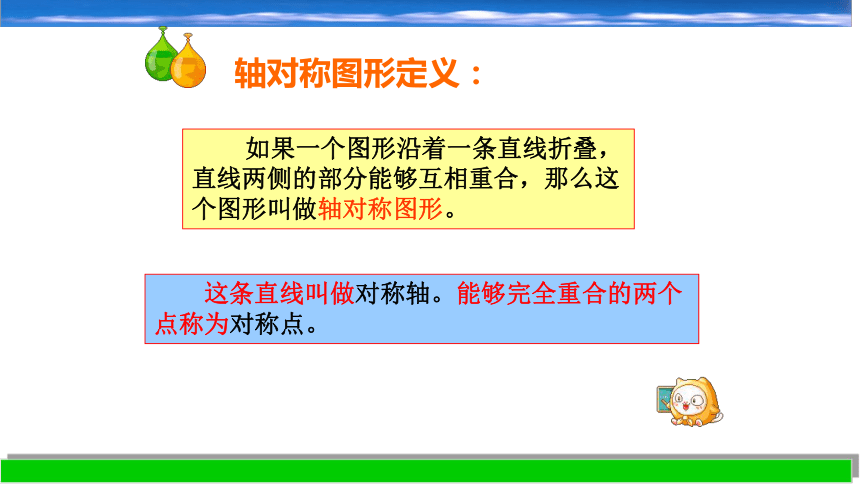
轴对称图形定义:
如果一个图形沿着一条直线折叠,直线两侧的部分能够互相重合,那么这个图形叫做轴对称图形。
这条直线叫做对称轴。能够完全重合的两个点称为对称点。
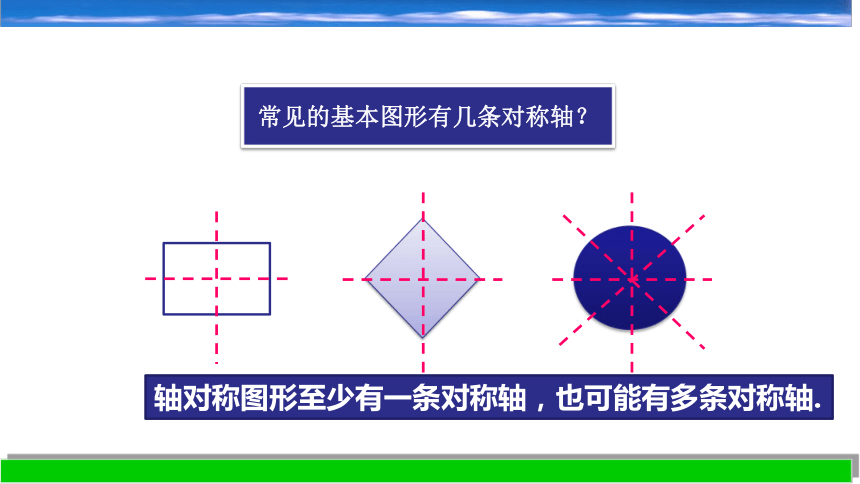
常见的基本图形有几条对称轴?
轴对称图形至少有一条对称轴,也可能有多条对称轴.
合作学习:
1、下列图形是轴对称图形吗?
判断方法:找出一条直线,把图形沿这条直线对折,看两侧的图形是否互相重合。
√
√
√
√
生活中的轴对称图形
如图,是由三个小正方形组成的图形,请你补画一个小正方形,使补画后的图形为轴对称图形,并画出对称轴。
请你试一试
1
2
3
请你试一试
合作学习:
2、如图,AD平分∠BAC,AB=AC.
(1) 四边形ABCD是轴对称图形吗?
请说出它的对称轴。
哪一点与点B对称?
(2) 连接BC,交AD于点E。把四边形ABDC沿AD对折,BE与CE重合吗? ∠AEC和 ∠AEB 呢?
A
B
C
D
解:∵ AD平分∠BAC
∴ ∠BAD = ∠CAD
E
当沿AD对折时,射线AB与射线AC重合
∵ AB=AC
∴ 点B与点C重合,点E与点E重合
∴ ∠AEC = ∠AEB = 90°
问题:对称轴AD与连结两个对称点之间的线段 BC有什么关系?
∴ BE与CE重合, ∠AEC与∠AEB重合
对称轴垂直平分两个对称点之间的线段。
画一画:分别画出下列轴对称图形的对称轴
对称轴垂直平分两个对称点之间的线段。
A
B
C
D
m
解:作线段AB的垂直平分线m,
直线m就是所求的对称轴。
解:作线段CD的垂直平分线n,
直线n就是所求的对称轴。
n
E
F
E′
F′
找对称轴的方法:先找到一对对称点,然后作两对称点连结线段的垂直平分线,该垂直平分线即为所求的对称轴。
思考:怎样找出点E和点F的对称点?
已知对称轴 l 和一个点A,如何画出点A关于 l 的对称点A′
A
A′
B
l
思考:
如何画线段AB关于直线l 的对称线段A′B′
A
B
A’
B’
B’
A’
如何画 △ABC关于直线l的对称图形
A
B
C
C’
先找( ),然后作出其( ),
最后顺次连接( )构成三角形.
特殊点
对称点
对称点
经验归纳:
刚才我们研究了一个图形具有轴对称的特征,你想不想看看两个图形是否也具有这样的特征呢?
一个图形
两个图形
请认真观察!
每一组里,左边的图形沿直线对折后与右边的图形完全重合吗?
同时,如果把作图沿直线m折叠,那么△A B C 和△ABC重合,这时,我们说△A B C 与△ABC关于直线m成轴对称.
一般地,有一个图形变为另一个图形,并使这两个图形沿某一条直线折叠后能够相互重合,这样的图形改变叫做图形的轴对称,这条直线叫做对称轴.
3.图形的轴对称的概念
成轴对称的两个图形是全等图形.
轴对称图形和两个图形成轴对称的区别与联系
轴对称图形
轴对称
区别
联系
图形
(1)轴对称图形是指( )
具有特殊形状的图形,
只对( ) 图形而言;
(2)对称轴( ) 只有一条
(1)轴对称是指( )图形
的位置关系,必须涉及
( )图形;
(2)只有( )对称轴.
如果把轴对称图形沿对称轴
分成两部分,那么这两个图形
就关于这条直线成轴对称.
如果把两个成轴对称的图形
拼在一起看成一个整体,那
么它就是一个轴对称图形.
一个
一个
不一定
两个
两个
一条
共同点
沿一条直线对折,对折的两部分能够完全重合
两个图形成
例2 如图,直线 l表示草原上的一条河流.一骑马少年从A地出发,去河边饮水,然后返回位于B地的家中.他沿怎样的路线行走,能使路程最短?做出这条最短路线.
将军饮马问题
解 如图,作点A关于直线l的对称点A ,连接A B,交直线 l
于点C,连接AC.骑马少年沿折线 A-C-B的路线行走时路程最短.
证明
设 P 是直线 l 上任意一点,连接AP,A P.
由作图知,直线 l 垂直平分AA ,
则AC= A C , AP=A P (线段垂直平分线上的点
到线段两端的距离相等).
∴AP+BP= A P+BP ≥ A B ,
A B= A C+BC=AC+BC ,
即AP+BP ≥ AC+BC ,
所以沿折线 A-C-B 的路线行走时路程最短.
C
P
方法技巧:利用关于直
线作对称点,将折线问
题转化为直线问题,运
用三边关系求解.
课堂总结
通过本节课的学习,你有什么收获?
1. 轴对称图形的概念
2. 两个图形成轴对称的概念
3. 两者的区别与联系
4. 找轴对称图形的对称轴及对应点
2.1图形的轴对称
2.1轴对称图形
问题情境:
A
B
(1)
(2)
将线段AB沿它的垂直平分线折起来,那么直线两旁的部分会重合吗?
A
O
B
将∠AOB沿它的平分线所在的直线折起来,那么直线两旁的部分会重合吗?
这些图形有什么共同的特征?
图形沿着一条直线对折,两侧的图形能够完全重合
轴
对
称
图
形
A
B
A
O
B
轴对称图形定义:
如果一个图形沿着一条直线折叠,直线两侧的部分能够互相重合,那么这个图形叫做轴对称图形。
这条直线叫做对称轴。能够完全重合的两个点称为对称点。
常见的基本图形有几条对称轴?
轴对称图形至少有一条对称轴,也可能有多条对称轴.
合作学习:
1、下列图形是轴对称图形吗?
判断方法:找出一条直线,把图形沿这条直线对折,看两侧的图形是否互相重合。
√
√
√
√
生活中的轴对称图形
如图,是由三个小正方形组成的图形,请你补画一个小正方形,使补画后的图形为轴对称图形,并画出对称轴。
请你试一试
1
2
3
请你试一试
合作学习:
2、如图,AD平分∠BAC,AB=AC.
(1) 四边形ABCD是轴对称图形吗?
请说出它的对称轴。
哪一点与点B对称?
(2) 连接BC,交AD于点E。把四边形ABDC沿AD对折,BE与CE重合吗? ∠AEC和 ∠AEB 呢?
A
B
C
D
解:∵ AD平分∠BAC
∴ ∠BAD = ∠CAD
E
当沿AD对折时,射线AB与射线AC重合
∵ AB=AC
∴ 点B与点C重合,点E与点E重合
∴ ∠AEC = ∠AEB = 90°
问题:对称轴AD与连结两个对称点之间的线段 BC有什么关系?
∴ BE与CE重合, ∠AEC与∠AEB重合
对称轴垂直平分两个对称点之间的线段。
画一画:分别画出下列轴对称图形的对称轴
对称轴垂直平分两个对称点之间的线段。
A
B
C
D
m
解:作线段AB的垂直平分线m,
直线m就是所求的对称轴。
解:作线段CD的垂直平分线n,
直线n就是所求的对称轴。
n
E
F
E′
F′
找对称轴的方法:先找到一对对称点,然后作两对称点连结线段的垂直平分线,该垂直平分线即为所求的对称轴。
思考:怎样找出点E和点F的对称点?
已知对称轴 l 和一个点A,如何画出点A关于 l 的对称点A′
A
A′
B
l
思考:
如何画线段AB关于直线l 的对称线段A′B′
A
B
A’
B’
B’
A’
如何画 △ABC关于直线l的对称图形
A
B
C
C’
先找( ),然后作出其( ),
最后顺次连接( )构成三角形.
特殊点
对称点
对称点
经验归纳:
刚才我们研究了一个图形具有轴对称的特征,你想不想看看两个图形是否也具有这样的特征呢?
一个图形
两个图形
请认真观察!
每一组里,左边的图形沿直线对折后与右边的图形完全重合吗?
同时,如果把作图沿直线m折叠,那么△A B C 和△ABC重合,这时,我们说△A B C 与△ABC关于直线m成轴对称.
一般地,有一个图形变为另一个图形,并使这两个图形沿某一条直线折叠后能够相互重合,这样的图形改变叫做图形的轴对称,这条直线叫做对称轴.
3.图形的轴对称的概念
成轴对称的两个图形是全等图形.
轴对称图形和两个图形成轴对称的区别与联系
轴对称图形
轴对称
区别
联系
图形
(1)轴对称图形是指( )
具有特殊形状的图形,
只对( ) 图形而言;
(2)对称轴( ) 只有一条
(1)轴对称是指( )图形
的位置关系,必须涉及
( )图形;
(2)只有( )对称轴.
如果把轴对称图形沿对称轴
分成两部分,那么这两个图形
就关于这条直线成轴对称.
如果把两个成轴对称的图形
拼在一起看成一个整体,那
么它就是一个轴对称图形.
一个
一个
不一定
两个
两个
一条
共同点
沿一条直线对折,对折的两部分能够完全重合
两个图形成
例2 如图,直线 l表示草原上的一条河流.一骑马少年从A地出发,去河边饮水,然后返回位于B地的家中.他沿怎样的路线行走,能使路程最短?做出这条最短路线.
将军饮马问题
解 如图,作点A关于直线l的对称点A ,连接A B,交直线 l
于点C,连接AC.骑马少年沿折线 A-C-B的路线行走时路程最短.
证明
设 P 是直线 l 上任意一点,连接AP,A P.
由作图知,直线 l 垂直平分AA ,
则AC= A C , AP=A P (线段垂直平分线上的点
到线段两端的距离相等).
∴AP+BP= A P+BP ≥ A B ,
A B= A C+BC=AC+BC ,
即AP+BP ≥ AC+BC ,
所以沿折线 A-C-B 的路线行走时路程最短.
C
P
方法技巧:利用关于直
线作对称点,将折线问
题转化为直线问题,运
用三边关系求解.
课堂总结
通过本节课的学习,你有什么收获?
1. 轴对称图形的概念
2. 两个图形成轴对称的概念
3. 两者的区别与联系
4. 找轴对称图形的对称轴及对应点
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
