浙教版八年级上册2.4等腰三角形的性质定理课件(共17张PPT)
文档属性
| 名称 | 浙教版八年级上册2.4等腰三角形的性质定理课件(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 696.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-23 16:45:04 | ||
图片预览

文档简介
(共17张PPT)
2.4 等腰三角形的判定定理
合作探究,自主学习
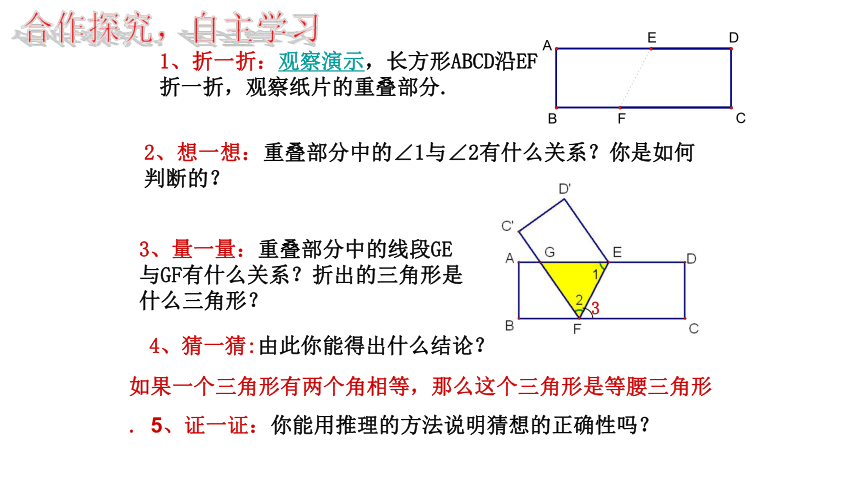
1、折一折:观察演示,长方形ABCD沿EF折一折,观察纸片的重叠部分.
4、猜一猜:由此你能得出什么结论?
3、量一量:重叠部分中的线段GE与GF有什么关系?折出的三角形是什么三角形?
2、想一想:重叠部分中的∠1与∠2有什么关系?你是如何判断的?
如果一个三角形有两个角相等,那么这个三角形是等腰三角形
. 5、证一证:你能用推理的方法说明猜想的正确性吗?
3
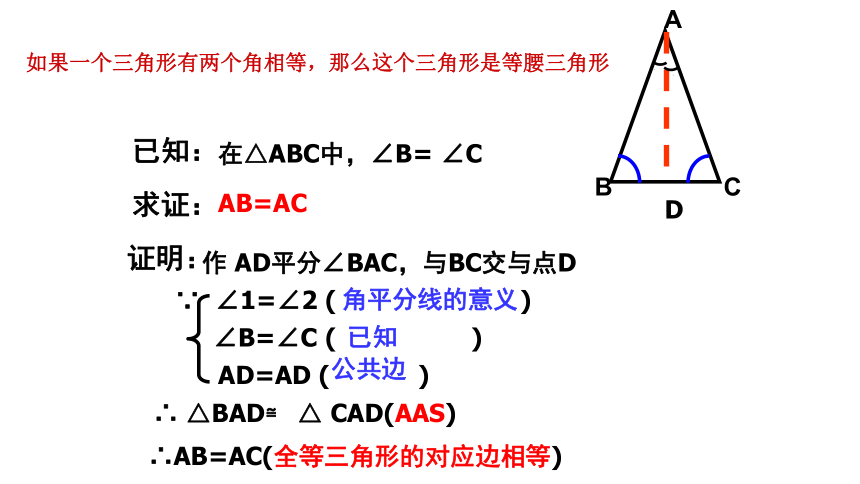
已知:
在△ABC中,∠B= ∠C
求证:
AB=AC
证明:
A
B
C
作 AD平分∠BAC,与BC交与点D
∴ △ BAD≌ △ CAD(AAS)
∴AB=AC(全等三角形的对应边相等)
D
∵ ∠1=∠2 ( )
∠B=∠C ( )
AD=AD ( )
公共边
已知
角平分线的意义
1
2
如果一个三角形有两个角相等,那么这个三角形是等腰三角形
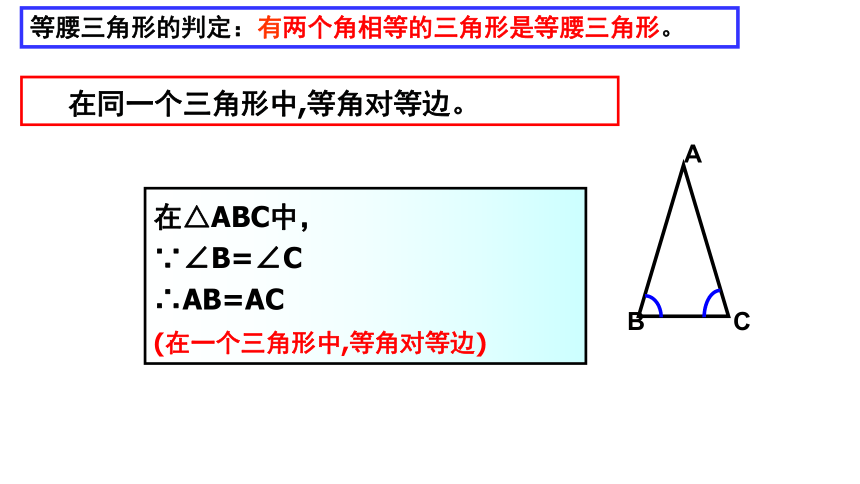
在同一个三角形中,等角对等边。
等腰三角形的判定:有两个角相等的三角形是等腰三角形。
在△ABC中,
∵∠B=∠C
∴AB=AC
(在一个三角形中,等角对等边)
A
B
C
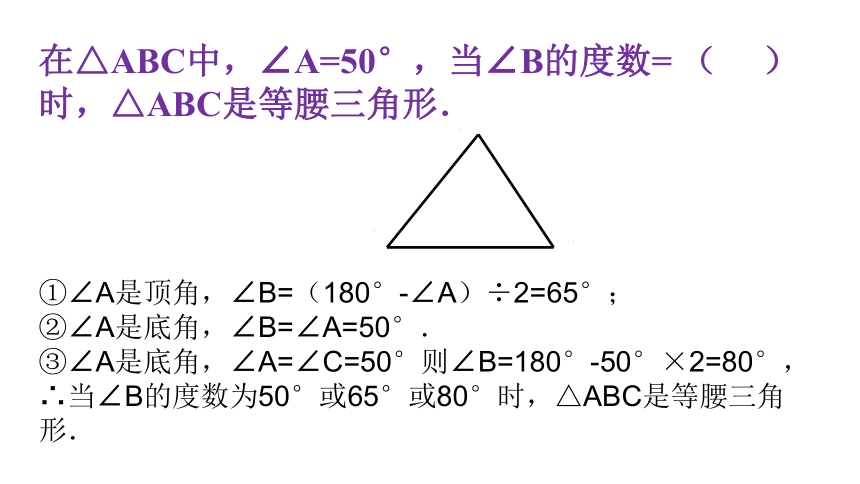
在△ABC中,∠A=50°,当∠B的度数= ( ) 时,△ABC是等腰三角形.
①∠A是顶角,∠B=(180°-∠A)÷2=65°;
②∠A是底角,∠B=∠A=50°.
③∠A是底角,∠A=∠C=50°则∠B=180°-50°×2=80°,
∴当∠B的度数为50°或65°或80°时,△ABC是等腰三角形.
A
B
C
例题讲解
B
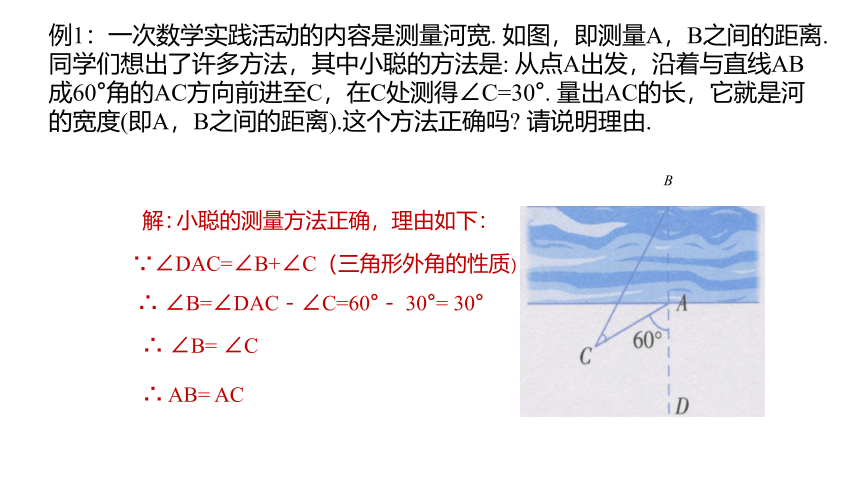
例1:一次数学实践活动的内容是测量河宽. 如图,即测量A,B之间的距离. 同学们想出了许多方法,其中小聪的方法是: 从点A出发,沿着与直线AB成60°角的AC方向前进至C,在C处测得∠C=30°. 量出AC的长,它就是河的宽度(即A,B之间的距离).这个方法正确吗 请说明理由.
∵∠DAC=∠B+∠C(三角形外角的性质)
∴ ∠B=∠DAC-∠C=60°- 30°= 30°
解:
小聪的测量方法正确,理由如下:
∴ ∠B= ∠C
∴ AB= AC
当课本作业课本题堂练习
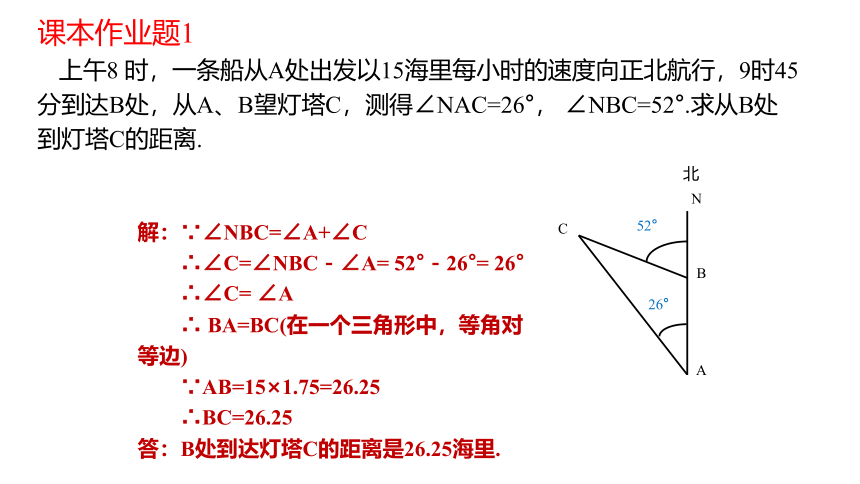
解:∵∠NBC=∠A+∠C
∴∠C=∠NBC-∠A= 52°-26°= 26°
∴∠C= ∠A
∴ BA=BC(在一个三角形中,等角对等边)
∵AB=15×1.75=26.25
∴BC=26.25
答:B处到达灯塔C的距离是26.25海里.
课本作业题1
上午8 时,一条船从A处出发以15海里每小时的速度向正北航行,9时45分到达B处,从A、B望灯塔C,测得∠NAC=26°, ∠NBC=52°.求从B处到灯塔C的距离.
N
B
A
C
52°
26°
北
4.如图,BD是等腰三角形ABC的底边AC上的高线,DE∥BC,交AB于点E.判断△BDE是不是等腰三角形,并证明你的判断.
课本作业题4.
如图,BD是等腰三角形ABC的底边AC上的高线,DE∥BC,交AB于点E.判断△BDE是不是等腰三角形,并证明你的判断.
等边三角形的三个角有什么性质?
在等腰三角形中,有一种特殊的情况,就是底边与腰相等,这时,三角形三边相等。
我们把三条边都相等的三角形
叫做等边三角形(正三角形)。
探索思考
想一想:
1、三个角都相等的三角形是等边三角形吗?
∵∠A=∠B=∠C=60 °
∴AB=AC=BC (为什么?)
∴三角形△ABC是等边三角形.
A
C
B
2、有一个角等于60 °的等腰三角形是等边三角形吗?
假若AB=AC.则∠B=∠C
当顶角∠A=60 °时,
∠B=∠C=60 °
∴∠A=∠B=∠C=60 °
∴ △ABC是等边三角形.
当底角∠B=60时,∠C=60 °
∠A=180°—(60°+60°)=60°
∴ ∠A=∠B=∠C=60 °
∴ △ABC是等边三角形.
A
C
B
1、三边相等的三角形是等边三角形.
等边三角形的判定方法:
3、有一个角等于60°的等腰三角形是等边三角形.
2、三个角都相等的三角形是等边三角形.
A
B
C
D
F
E
3
1
2
如图, △ABC为等边三角形, ∠ 1= ∠ 2= ∠ 3
(1)求∠ BEC的度数.
(2) △ DEF为等边三角形吗 为什么
名称 图 形 概 念 性质与边角关系 判 定
等 腰 三 角 形
A
B
C
有两边相等的三角形是等腰三角形
2.等边对等角
3. 三线合一
4.是轴对称图形
2.等角对等边
1.两边相等
1.两腰相等
小 结
在△ABC中,已知 AB =AC ,BG平分∠ABC,CG平分∠ACB.过点G作直线EF//BC交AB于E,交AC于F.
(2)线段EF和线段EB,FC之间有没有关系 若有,那么是什么关系
F
E
G
B
C
A
B
G
C
A
E
F
AB≠AC
(1)请问图中有多少个等腰三角形 说明理由.
思考题
探究性问题
如图所示,已知下列两个三角形,思考
怎样把每个三角形只剪一次,将它分成两个
等腰三角形?试一试,你一定会成功的。
120°
20 °
40 °
100 °
20 °
60 °
120°
20 °
40 °
20 °
100 °
20 °
60 °
20 °
拓展提高:如图,已知△ABC中,AB=AC,D、E分别是AB和BC上的点,连接DE并延长与AC的延长线交于点F,若DE=EF,求证:BD=CF.
证明:过D作DG∥AF交BC于G,
则∠F=∠GDE,DE=EF,∠DEG=∠FEC
∴△DGE≌△FCE(ASA),
∴GD=CF,
∵AB=AC,
∴∠B=∠ACB,
又∵DG∥AF,
∴∠ACB=∠BGD,
∴∠B=∠BGD,∴BD=GD,
又∵GD=CF,∴BD=CF.
2.4 等腰三角形的判定定理
合作探究,自主学习
1、折一折:观察演示,长方形ABCD沿EF折一折,观察纸片的重叠部分.
4、猜一猜:由此你能得出什么结论?
3、量一量:重叠部分中的线段GE与GF有什么关系?折出的三角形是什么三角形?
2、想一想:重叠部分中的∠1与∠2有什么关系?你是如何判断的?
如果一个三角形有两个角相等,那么这个三角形是等腰三角形
. 5、证一证:你能用推理的方法说明猜想的正确性吗?
3
已知:
在△ABC中,∠B= ∠C
求证:
AB=AC
证明:
A
B
C
作 AD平分∠BAC,与BC交与点D
∴ △ BAD≌ △ CAD(AAS)
∴AB=AC(全等三角形的对应边相等)
D
∵ ∠1=∠2 ( )
∠B=∠C ( )
AD=AD ( )
公共边
已知
角平分线的意义
1
2
如果一个三角形有两个角相等,那么这个三角形是等腰三角形
在同一个三角形中,等角对等边。
等腰三角形的判定:有两个角相等的三角形是等腰三角形。
在△ABC中,
∵∠B=∠C
∴AB=AC
(在一个三角形中,等角对等边)
A
B
C
在△ABC中,∠A=50°,当∠B的度数= ( ) 时,△ABC是等腰三角形.
①∠A是顶角,∠B=(180°-∠A)÷2=65°;
②∠A是底角,∠B=∠A=50°.
③∠A是底角,∠A=∠C=50°则∠B=180°-50°×2=80°,
∴当∠B的度数为50°或65°或80°时,△ABC是等腰三角形.
A
B
C
例题讲解
B
例1:一次数学实践活动的内容是测量河宽. 如图,即测量A,B之间的距离. 同学们想出了许多方法,其中小聪的方法是: 从点A出发,沿着与直线AB成60°角的AC方向前进至C,在C处测得∠C=30°. 量出AC的长,它就是河的宽度(即A,B之间的距离).这个方法正确吗 请说明理由.
∵∠DAC=∠B+∠C(三角形外角的性质)
∴ ∠B=∠DAC-∠C=60°- 30°= 30°
解:
小聪的测量方法正确,理由如下:
∴ ∠B= ∠C
∴ AB= AC
当课本作业课本题堂练习
解:∵∠NBC=∠A+∠C
∴∠C=∠NBC-∠A= 52°-26°= 26°
∴∠C= ∠A
∴ BA=BC(在一个三角形中,等角对等边)
∵AB=15×1.75=26.25
∴BC=26.25
答:B处到达灯塔C的距离是26.25海里.
课本作业题1
上午8 时,一条船从A处出发以15海里每小时的速度向正北航行,9时45分到达B处,从A、B望灯塔C,测得∠NAC=26°, ∠NBC=52°.求从B处到灯塔C的距离.
N
B
A
C
52°
26°
北
4.如图,BD是等腰三角形ABC的底边AC上的高线,DE∥BC,交AB于点E.判断△BDE是不是等腰三角形,并证明你的判断.
课本作业题4.
如图,BD是等腰三角形ABC的底边AC上的高线,DE∥BC,交AB于点E.判断△BDE是不是等腰三角形,并证明你的判断.
等边三角形的三个角有什么性质?
在等腰三角形中,有一种特殊的情况,就是底边与腰相等,这时,三角形三边相等。
我们把三条边都相等的三角形
叫做等边三角形(正三角形)。
探索思考
想一想:
1、三个角都相等的三角形是等边三角形吗?
∵∠A=∠B=∠C=60 °
∴AB=AC=BC (为什么?)
∴三角形△ABC是等边三角形.
A
C
B
2、有一个角等于60 °的等腰三角形是等边三角形吗?
假若AB=AC.则∠B=∠C
当顶角∠A=60 °时,
∠B=∠C=60 °
∴∠A=∠B=∠C=60 °
∴ △ABC是等边三角形.
当底角∠B=60时,∠C=60 °
∠A=180°—(60°+60°)=60°
∴ ∠A=∠B=∠C=60 °
∴ △ABC是等边三角形.
A
C
B
1、三边相等的三角形是等边三角形.
等边三角形的判定方法:
3、有一个角等于60°的等腰三角形是等边三角形.
2、三个角都相等的三角形是等边三角形.
A
B
C
D
F
E
3
1
2
如图, △ABC为等边三角形, ∠ 1= ∠ 2= ∠ 3
(1)求∠ BEC的度数.
(2) △ DEF为等边三角形吗 为什么
名称 图 形 概 念 性质与边角关系 判 定
等 腰 三 角 形
A
B
C
有两边相等的三角形是等腰三角形
2.等边对等角
3. 三线合一
4.是轴对称图形
2.等角对等边
1.两边相等
1.两腰相等
小 结
在△ABC中,已知 AB =AC ,BG平分∠ABC,CG平分∠ACB.过点G作直线EF//BC交AB于E,交AC于F.
(2)线段EF和线段EB,FC之间有没有关系 若有,那么是什么关系
F
E
G
B
C
A
B
G
C
A
E
F
AB≠AC
(1)请问图中有多少个等腰三角形 说明理由.
思考题
探究性问题
如图所示,已知下列两个三角形,思考
怎样把每个三角形只剪一次,将它分成两个
等腰三角形?试一试,你一定会成功的。
120°
20 °
40 °
100 °
20 °
60 °
120°
20 °
40 °
20 °
100 °
20 °
60 °
20 °
拓展提高:如图,已知△ABC中,AB=AC,D、E分别是AB和BC上的点,连接DE并延长与AC的延长线交于点F,若DE=EF,求证:BD=CF.
证明:过D作DG∥AF交BC于G,
则∠F=∠GDE,DE=EF,∠DEG=∠FEC
∴△DGE≌△FCE(ASA),
∴GD=CF,
∵AB=AC,
∴∠B=∠ACB,
又∵DG∥AF,
∴∠ACB=∠BGD,
∴∠B=∠BGD,∴BD=GD,
又∵GD=CF,∴BD=CF.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
