浙教版八年级上册2.7.探索勾股定理(共18张PPT)
文档属性
| 名称 | 浙教版八年级上册2.7.探索勾股定理(共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 519.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-24 13:58:35 | ||
图片预览





文档简介
(共18张PPT)
2.7 探索勾股定理(1)
一、情境引入
会标中央的图案是赵爽弦图,它与“勾股定理”有关,数学家还曾建议用“勾股定理”的图来作为与“外星人”联系的信号.
如图是在北京召开的第24届国际数学家大会(ICM—2002) 的会标.它的设计思路可追溯到3世纪中国数学家赵爽所使用的弦图.用弦图证明勾股定理在数学史上有着重要的地位.
在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
中国数学家赵爽根据弦图给出了勾股定理的一种证明
勾
股
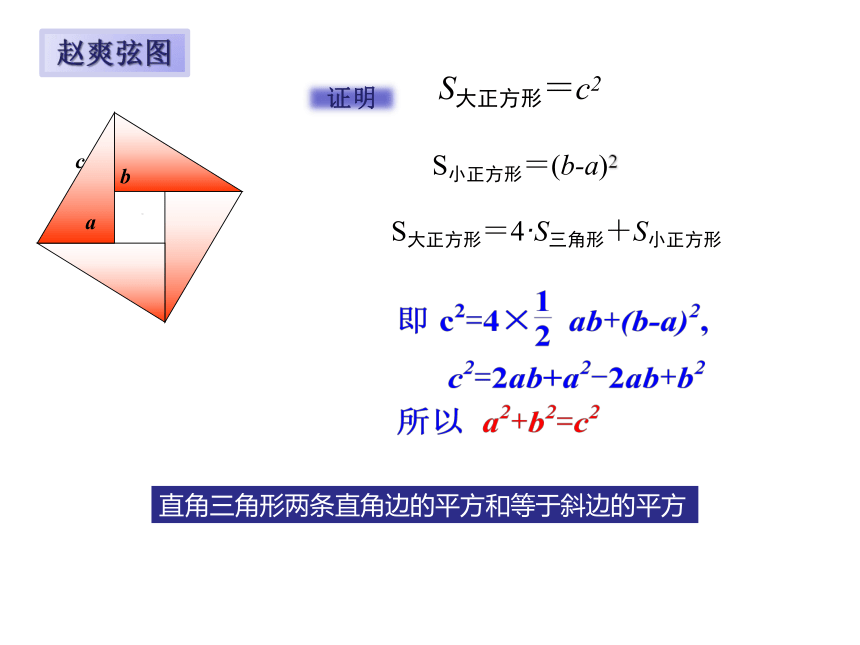
赵爽弦图
a
b
c
b-a
S大正方形=c2
S小正方形=(b-a)2
S大正方形=4·S三角形+S小正方形
证明
直角三角形两条直角边的平方和等于斜边的平方
大正方形的面积可以表示为 ;
也可以表示为 .
(a+b)2
c2 +4 ab
∵ (a+b)2 = c2 + 4 ab
a2+2ab+b2 = c2 +2ab
∴ a2+b2=c2
面积证法2: 用四个全等的直角三角形,还可以拼成如图所示的图形,你能否根据这一图形,证明勾股定理.
a
a
a
a
b
b
b
b
c
c
c
c
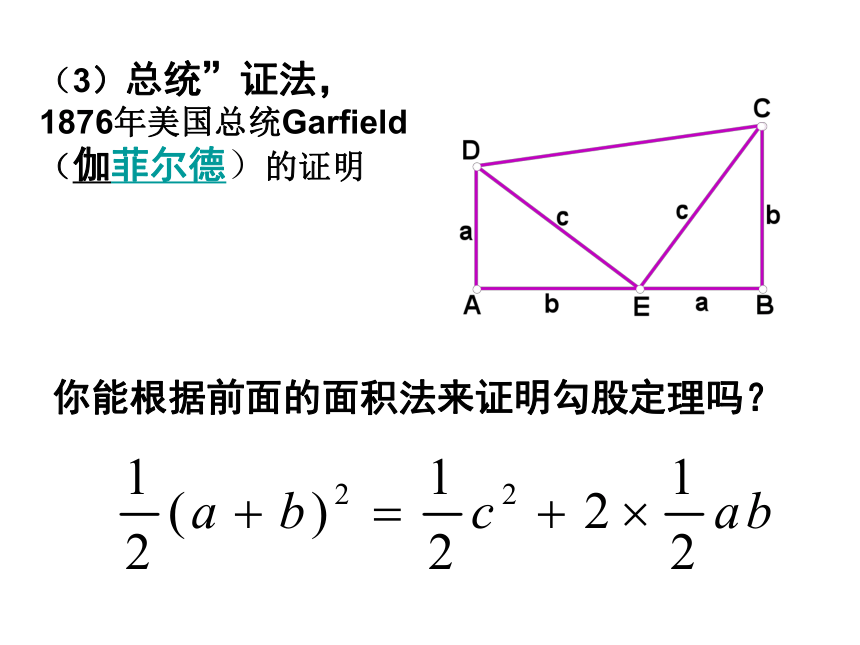
(3)总统”证法, 1876年美国总统Garfield(伽菲尔德)的证明
你能根据前面的面积法来证明勾股定理吗?
勾股定理
如果直角三角形两直角边分别为a、b,斜边为c,那么
即 直角三角形两直角边的平方和等于斜边的平方.
a
b
c
结论:
1、下图中的三角形是直角三角形,其余是正方形,求下列图中字母所表示的正方形的面积.
125
25
100
A
225
81
B
144
练一练
A
B
C
D
7cm
2、如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积之和为___________cm2。
49
(1)若a=3, b=2, 求c;
例1:已知ΔABC中,∠C=Rt∠,BC=a,
AC=b,AB=c。
(2)若a=15,c=17,求b;
(3)若c=10,a:b=3:4,求a、b;
可用勾股定理建立方程.
方法小结:
变一变:若Rt△ABC的两边为1和2,第三边为多少?
x
例2、如图,你能计算出下列直角三角形中未知边的长吗?
2
反思:若要你在数轴上准确表示 ,你会参考上面的结果画吗?
小结:利用勾股定理可以解决直角三角形的边长。
-1
0
1
2
1
x
0
2
解:由勾股定理得x =1 +2 =5
∵x>0
∴x=
解:由勾股定理得x =2 -1 =3
∵x>0
∴x=
例3、如图:是一个长方形零件图,根据所给的尺寸,求两孔中心A、B之间的距离。
A
B
C
40
90
160
40
解:过A作铅垂线,过B作水平线,两线交于点C,则∠C =90。
AC=90-40=50(mm),
BC=160-40=120(mm).
∵ ∠C =90。
∴ AB2=AC2+BC2
∵AB>0
∴AB=130(mm)
答:两孔中心A,B之间的距离为130mm.
说说你对本题的收获
温馨提示:在实际问题中,要会根据需要构造直角三角形,再通过勾股定理来解决问题。
=502+1202
=16900(mm2)
C
A
B
y=0
生活应用一
求c
a=4
b=3
受台风菲特影响,王叔叔家的一棵树在离地面4米处断裂,树的顶部落在离树跟底部3米处,他想知道这棵树折断前有多高?
如图,校园内有两棵树,相距8米,一棵树树高13米,另一棵树高7米,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞多少米?
y=0
生活应用二
温馨提示:在实际问题中,要会根据需要构造直角三角形,再通过勾股定理来解决问题.
在波平如镜的湖面上,有一朵美丽的红莲 ,它高出水面1米 ,一阵大风吹过,红莲被吹至一边,花朵齐及水面,如果知道红莲移动的水平距离为2米 ,问这里水深多少
x+1
B
C
A
H
1
2
┓
x
x2+22=(x+1)2
解开疑惑
(1)求墙的高度
解:
∴AC=
∵∠ACB=90°AB=3,BC=1
=
=
(2)若梯子的底端将向外水平移动1米,
求梯子顶端下滑多少米
A
A′
B
B′
3m
1m
C
∴ AB2=AC2+BC2
有一架3米长的梯子靠在学校围墙上,刚好与墙头对齐,此时梯脚B与墙脚C的距离是1米。
探究
小结
你学会了什么?
勾股定理
(a2+b2=c2)
直角三角形
中的应用
已知任意两条边,
就可以求第三边.
已知一条边,以及另
两条边之间的关系,
就可以求另两条边的
长度.
课后思考题:
在△ABC中,∠BAC=120°,AB=AC= cm,
一动点P从B向C以每秒2cm的速度移动,
问当P点移动多少秒时,PA与腰垂直?
2.7 探索勾股定理(1)
一、情境引入
会标中央的图案是赵爽弦图,它与“勾股定理”有关,数学家还曾建议用“勾股定理”的图来作为与“外星人”联系的信号.
如图是在北京召开的第24届国际数学家大会(ICM—2002) 的会标.它的设计思路可追溯到3世纪中国数学家赵爽所使用的弦图.用弦图证明勾股定理在数学史上有着重要的地位.
在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
中国数学家赵爽根据弦图给出了勾股定理的一种证明
勾
股
赵爽弦图
a
b
c
b-a
S大正方形=c2
S小正方形=(b-a)2
S大正方形=4·S三角形+S小正方形
证明
直角三角形两条直角边的平方和等于斜边的平方
大正方形的面积可以表示为 ;
也可以表示为 .
(a+b)2
c2 +4 ab
∵ (a+b)2 = c2 + 4 ab
a2+2ab+b2 = c2 +2ab
∴ a2+b2=c2
面积证法2: 用四个全等的直角三角形,还可以拼成如图所示的图形,你能否根据这一图形,证明勾股定理.
a
a
a
a
b
b
b
b
c
c
c
c
(3)总统”证法, 1876年美国总统Garfield(伽菲尔德)的证明
你能根据前面的面积法来证明勾股定理吗?
勾股定理
如果直角三角形两直角边分别为a、b,斜边为c,那么
即 直角三角形两直角边的平方和等于斜边的平方.
a
b
c
结论:
1、下图中的三角形是直角三角形,其余是正方形,求下列图中字母所表示的正方形的面积.
125
25
100
A
225
81
B
144
练一练
A
B
C
D
7cm
2、如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积之和为___________cm2。
49
(1)若a=3, b=2, 求c;
例1:已知ΔABC中,∠C=Rt∠,BC=a,
AC=b,AB=c。
(2)若a=15,c=17,求b;
(3)若c=10,a:b=3:4,求a、b;
可用勾股定理建立方程.
方法小结:
变一变:若Rt△ABC的两边为1和2,第三边为多少?
x
例2、如图,你能计算出下列直角三角形中未知边的长吗?
2
反思:若要你在数轴上准确表示 ,你会参考上面的结果画吗?
小结:利用勾股定理可以解决直角三角形的边长。
-1
0
1
2
1
x
0
2
解:由勾股定理得x =1 +2 =5
∵x>0
∴x=
解:由勾股定理得x =2 -1 =3
∵x>0
∴x=
例3、如图:是一个长方形零件图,根据所给的尺寸,求两孔中心A、B之间的距离。
A
B
C
40
90
160
40
解:过A作铅垂线,过B作水平线,两线交于点C,则∠C =90。
AC=90-40=50(mm),
BC=160-40=120(mm).
∵ ∠C =90。
∴ AB2=AC2+BC2
∵AB>0
∴AB=130(mm)
答:两孔中心A,B之间的距离为130mm.
说说你对本题的收获
温馨提示:在实际问题中,要会根据需要构造直角三角形,再通过勾股定理来解决问题。
=502+1202
=16900(mm2)
C
A
B
y=0
生活应用一
求c
a=4
b=3
受台风菲特影响,王叔叔家的一棵树在离地面4米处断裂,树的顶部落在离树跟底部3米处,他想知道这棵树折断前有多高?
如图,校园内有两棵树,相距8米,一棵树树高13米,另一棵树高7米,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞多少米?
y=0
生活应用二
温馨提示:在实际问题中,要会根据需要构造直角三角形,再通过勾股定理来解决问题.
在波平如镜的湖面上,有一朵美丽的红莲 ,它高出水面1米 ,一阵大风吹过,红莲被吹至一边,花朵齐及水面,如果知道红莲移动的水平距离为2米 ,问这里水深多少
x+1
B
C
A
H
1
2
┓
x
x2+22=(x+1)2
解开疑惑
(1)求墙的高度
解:
∴AC=
∵∠ACB=90°AB=3,BC=1
=
=
(2)若梯子的底端将向外水平移动1米,
求梯子顶端下滑多少米
A
A′
B
B′
3m
1m
C
∴ AB2=AC2+BC2
有一架3米长的梯子靠在学校围墙上,刚好与墙头对齐,此时梯脚B与墙脚C的距离是1米。
探究
小结
你学会了什么?
勾股定理
(a2+b2=c2)
直角三角形
中的应用
已知任意两条边,
就可以求第三边.
已知一条边,以及另
两条边之间的关系,
就可以求另两条边的
长度.
课后思考题:
在△ABC中,∠BAC=120°,AB=AC= cm,
一动点P从B向C以每秒2cm的速度移动,
问当P点移动多少秒时,PA与腰垂直?
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
