垂直(第四课时)(教案) 四年级下册数学 沪教版(表格式)
文档属性
| 名称 | 垂直(第四课时)(教案) 四年级下册数学 沪教版(表格式) |

|
|
| 格式 | zip | ||
| 文件大小 | 67.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-26 00:00:00 | ||
图片预览

文档简介
课题 垂直(第四课时) 课型 新授
教学 目标 理解点到直线的距离的概念。领悟“两点之间线段最短”、“点到直线的垂直线段最短”,知道两点之间的距离和点到直线的距离。 经历垂直线段的性质的探索过程,知道从直线外一点到已知直线所画的线段中垂直线段最短,知道点到直线的距离。 体会数学和现实生活的联系,进一步培养数学应用意识和学习数学的积极情感。
教学重点 会用三角尺按要求画出已知直线的垂线。
教学难点 掌握画垂线的一般步骤方法。
教学技术与学习资源应用: PPT课件,三角尺,量角器
教学 环节 目标指向 师生活动 评价 关注点
一、情境导入 师:今天让我们来到大海中去驾驶一辆游轮一起去探险,好吗?船长们,现在我们就出发! 出示:课本第60页的情景图 师:岛上的码头在P处,在陆地上选哪里造码头,到P的航程最短呢? 1、生能思考如何使航程最短。
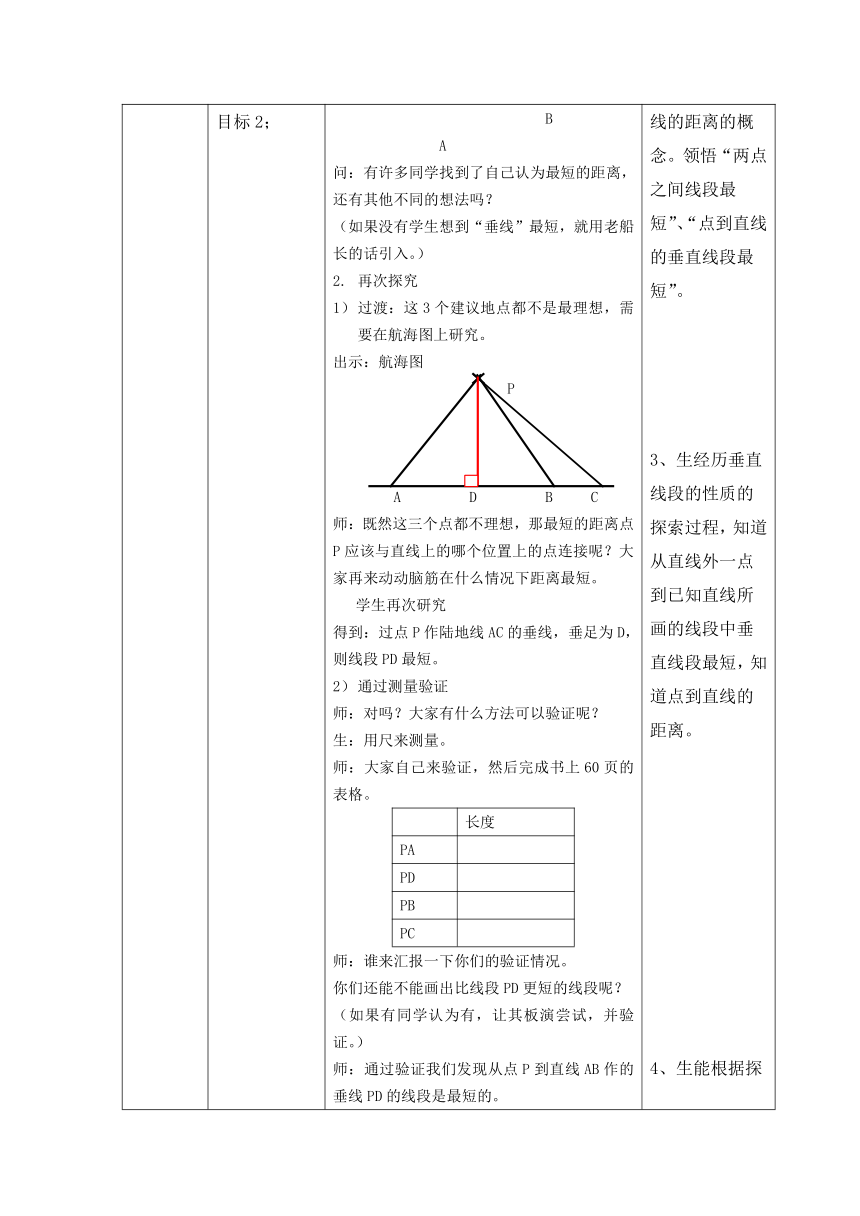
二、探究新知 1.对应教学目标1; 2.对应教学目标2; 尝试解决 师:如果把陆地用一条直线AB来表示,你们能不能找到点P到陆地的最短的距离呢?船长们,请你们自己试一试。 学生尝试,板演汇报 P C B A 问:有许多同学找到了自己认为最短的距离,还有其他不同的想法吗? (如果没有学生想到“垂线”最短,就用老船长的话引入。) 再次探究 过渡:这3个建议地点都不是最理想,需要在航海图上研究。 出示:航海图 P A D B C 师:既然这三个点都不理想,那最短的距离点P应该与直线上的哪个位置上的点连接呢?大家再来动动脑筋在什么情况下距离最短。 学生再次研究 得到:过点P作陆地线AC的垂线,垂足为D,则线段PD最短。 通过测量验证 师:对吗?大家有什么方法可以验证呢? 生:用尺来测量。 师:大家自己来验证,然后完成书上60页的表格。 长度PAPDPBPC
师:谁来汇报一下你们的验证情况。 你们还能不能画出比线段PD更短的线段呢? (如果有同学认为有,让其板演尝试,并验证。) 师:通过验证我们发现从点P到直线AB作的垂线PD的线段是最短的。 出示: P l 师:请大家过点P向直线l作出最短的距离的线段。 学生笔练 问:谁来介绍一下你是怎样画出最短的距离的? 生:从点P向直线作垂线PQ。 师:说得好!从直线l外一点P引直线l的垂线,垂足为Q,线段PQ叫做点P到直线l的距离。今天我们就来学习——点到直线的距离。 (出示课题:点到直线的距离) 跟进练习 量一量,线段PA、PB、PC各是多少厘米?哪一条是点P到直线l的距离? P l A B C 1、生能利用几何作图工具摆一摆,想一想,如何使距离最短。 2、理解点到直线的距离的概念。领悟“两点之间线段最短”、“点到直线的垂直线段最短”。 3、生经历垂直线段的性质的探索过程,知道从直线外一点到已知直线所画的线段中垂直线段最短,知道点到直线的距离。 4、生能根据探究结果总结“两点之间线段最短”、“点到直线的垂直线段最短”。 5、生能利用新知,通过画垂线来得出点到直线的距离。
三、延伸拓展 1.对应教学目标1; 2.对应教学目标3. 量一量,下图中点A到直线CD的距离。 D C A 师:怎样才能量出点A到直线的距离呢? 得到:要线从点A画直线CD的垂线,然后再量出点到直线的距离。 学生独立练习 量出下列点到直线l的距离。(课本第60页的练一练) 完成在书上 在航海图上有南长航线、三堡线。(探究50页的第3题) 1厘米表示1千米 从堡镇到三花岛有多少千米? 红色的航标到这两条航线的距离分别是多少千米? 三花岛、堡镇到南长航线的距离分别为多少千米? 1、生理解点到直线的距离的概念。领悟“两点之间线段最短”、“点到直线的垂直线段最短”,知道两点之间的距离和点到直线的距离。 2、生能根据题意,过点画垂线段,并得出点到直线的距离。
四、课堂总结 师:今天我们学习了——点到直线的距离,你还有什么疑问吗?
板 书 设 计 点到直线的距离 垂线段
教学 目标 理解点到直线的距离的概念。领悟“两点之间线段最短”、“点到直线的垂直线段最短”,知道两点之间的距离和点到直线的距离。 经历垂直线段的性质的探索过程,知道从直线外一点到已知直线所画的线段中垂直线段最短,知道点到直线的距离。 体会数学和现实生活的联系,进一步培养数学应用意识和学习数学的积极情感。
教学重点 会用三角尺按要求画出已知直线的垂线。
教学难点 掌握画垂线的一般步骤方法。
教学技术与学习资源应用: PPT课件,三角尺,量角器
教学 环节 目标指向 师生活动 评价 关注点
一、情境导入 师:今天让我们来到大海中去驾驶一辆游轮一起去探险,好吗?船长们,现在我们就出发! 出示:课本第60页的情景图 师:岛上的码头在P处,在陆地上选哪里造码头,到P的航程最短呢? 1、生能思考如何使航程最短。
二、探究新知 1.对应教学目标1; 2.对应教学目标2; 尝试解决 师:如果把陆地用一条直线AB来表示,你们能不能找到点P到陆地的最短的距离呢?船长们,请你们自己试一试。 学生尝试,板演汇报 P C B A 问:有许多同学找到了自己认为最短的距离,还有其他不同的想法吗? (如果没有学生想到“垂线”最短,就用老船长的话引入。) 再次探究 过渡:这3个建议地点都不是最理想,需要在航海图上研究。 出示:航海图 P A D B C 师:既然这三个点都不理想,那最短的距离点P应该与直线上的哪个位置上的点连接呢?大家再来动动脑筋在什么情况下距离最短。 学生再次研究 得到:过点P作陆地线AC的垂线,垂足为D,则线段PD最短。 通过测量验证 师:对吗?大家有什么方法可以验证呢? 生:用尺来测量。 师:大家自己来验证,然后完成书上60页的表格。 长度PAPDPBPC
师:谁来汇报一下你们的验证情况。 你们还能不能画出比线段PD更短的线段呢? (如果有同学认为有,让其板演尝试,并验证。) 师:通过验证我们发现从点P到直线AB作的垂线PD的线段是最短的。 出示: P l 师:请大家过点P向直线l作出最短的距离的线段。 学生笔练 问:谁来介绍一下你是怎样画出最短的距离的? 生:从点P向直线作垂线PQ。 师:说得好!从直线l外一点P引直线l的垂线,垂足为Q,线段PQ叫做点P到直线l的距离。今天我们就来学习——点到直线的距离。 (出示课题:点到直线的距离) 跟进练习 量一量,线段PA、PB、PC各是多少厘米?哪一条是点P到直线l的距离? P l A B C 1、生能利用几何作图工具摆一摆,想一想,如何使距离最短。 2、理解点到直线的距离的概念。领悟“两点之间线段最短”、“点到直线的垂直线段最短”。 3、生经历垂直线段的性质的探索过程,知道从直线外一点到已知直线所画的线段中垂直线段最短,知道点到直线的距离。 4、生能根据探究结果总结“两点之间线段最短”、“点到直线的垂直线段最短”。 5、生能利用新知,通过画垂线来得出点到直线的距离。
三、延伸拓展 1.对应教学目标1; 2.对应教学目标3. 量一量,下图中点A到直线CD的距离。 D C A 师:怎样才能量出点A到直线的距离呢? 得到:要线从点A画直线CD的垂线,然后再量出点到直线的距离。 学生独立练习 量出下列点到直线l的距离。(课本第60页的练一练) 完成在书上 在航海图上有南长航线、三堡线。(探究50页的第3题) 1厘米表示1千米 从堡镇到三花岛有多少千米? 红色的航标到这两条航线的距离分别是多少千米? 三花岛、堡镇到南长航线的距离分别为多少千米? 1、生理解点到直线的距离的概念。领悟“两点之间线段最短”、“点到直线的垂直线段最短”,知道两点之间的距离和点到直线的距离。 2、生能根据题意,过点画垂线段,并得出点到直线的距离。
四、课堂总结 师:今天我们学习了——点到直线的距离,你还有什么疑问吗?
板 书 设 计 点到直线的距离 垂线段
