1.3.1 证明 课件(共17张PPT)
文档属性
| 名称 | 1.3.1 证明 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 916.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-09 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
1.3.1 证明
浙教版 八年级上册
教学目标
教学目标:
1、了解证明的含义。
2、体验、理解证明的必要性和推理过程中要步步有据。
3、了解证明的表达格式,会按规定格式证明简单命题。
4、通过证明步骤中由命题画出图形,写出已知、求证的过程,继续训练学生由几何语句正确画出几何图形的能力。
重点:证明的含义和表述格式。
难点:按规定格式表述证明的过程。
新知导入
哦……那可
怎么办
【思考】如何证实一个命题是真命题呢?
用我们以前学过的观察,实验,验证特例等方法.
这些方法往往并不可靠.
那已经知道的真命题又是如何证实的
能不能根据已经知道的真命题证实呢
新知讲解
通过观察,先猜想结论,再动手验证:
(1)如图,一组直线a,b,c,d是否都互相平行
a
b
c
d
新知讲解
通过观察,先猜想结论,再动手验证:
(2)当n=0,1,2,3,4时,代数式n -3n+7的值分别是7,5,5,7,11,它们都是质数。那么,命题 “对于自然数n,代数式n -3n+7的值都是素数”是真命题吗
当n=6时, n -3n+7 =25不是素数
新知讲解
要判定一个命题是真命题,往往需要从命题的条件出发,根据已知的定义、基本事实、定理(包括推论),一步一步推得结论成立,这样的推理过程叫做证明 。
推 理
推理的过程叫证明
原名、公理
一些条件
+
新知讲解
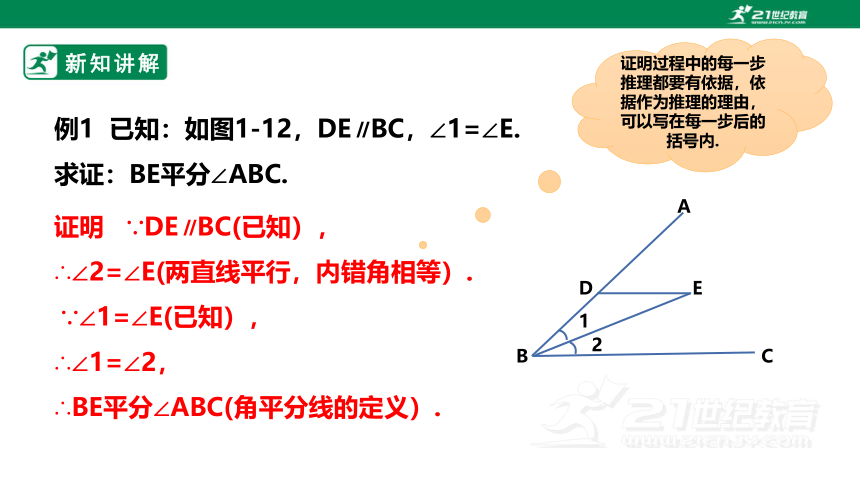
例1 已知:如图1-12,DE∥BC,∠1=∠E.
求证:BE平分∠ABC.
证明 ∵DE∥BC(已知),
∴∠2=∠E(两直线平行,内错角相等).
∵∠1=∠E(已知),
∴∠1=∠2,
∴BE平分∠ABC(角平分线的定义).
B
A
D
E
C
1
2
证明过程中的每一步推理都要有依据,依据作为推理的理由,可以写在每一步后的括号内.
新知讲解
例2 已知:如图,AB∥CD,EP,FP分别平分∠BEF,∠DFE.
求证:∠PEF+∠PFE=90°.
A
B
C
D
E
P
F
新知讲解
证明 ∵EP,FP分别平分∠BEF,∠DFE(已知),
∴∠PEF= ∠BEF,∠PFE= ∠DFE(角平分线的定义).
∵AB∥CD(已知),
∴∠BEF+∠DFE=180°(两直线平行,同旁内角互补).
∴∠PEF+∠PFE= ∠BEF+ ∠DFE= (∠BEF+∠DFE)=90°
例2 已知:如图,AB∥CD,EP,FP分别平分∠BEF,∠DFE.
求证:∠PEF+∠PFE=90°.
新知讲解
证明中的每一步推理都要有根据,这些根据可以是已知条件,
也可以是定义、基本事实、定理等.
课堂练习
1.关于证明,下列说法不正确的是( )
A.证明是说明命题是真命题的过程
B.要判定一个命题是真命题常常通过推理的方式
C.要说明一个命题是假命题常采用举反例的方式
D.真命题与假命题都可以通过举反例来说明
D
2.有一条直的宽纸带,按如图所示的方式折叠,则∠α的度数等于( )
A.50° B.60°
C.75° D.85°
C
课堂练习
3.如图,田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是( )
A.垂线段最短
B.经过一点有无数条直线
C.经过两点,有且仅有一条直线
D.两点之间,线段最短
D
4.如图,若AO⊥CO,BO⊥DO,则∠AOB=∠COD,推理的理由是( )
A.同角的补角相等 B.同角的余角相等
C.AO⊥CO D.BO⊥DO
B
∴________∥________
( ).
∴AB∥CD.
课堂练习
5.补充完成下列证明,并填上推理的依据.
已知:如图,AB⊥BC,EF⊥BC,∠1=∠2.
求证:AB∥CD.
证明:∵AB⊥BC,
∴∠ABC=________( ).
90°
垂直的定义
∵EF⊥BC( ),
∴∠FEC=________( ).
∴∠ABC=∠FEC( ).
∴________∥________( ).
∵∠1=∠2,
已知
90°
垂直的定义
等量代换
AB
EF
同位角相等,两直线平行
EF
CD
内错角相等,两直线平行
课堂练习
6.已知:如图,AD⊥BC于D,EG⊥BC于G,∠E=∠1.
求证:AD平分∠BAC.
解:如图,∵AD⊥BC,EG⊥BC(已知),
∴∠4=∠5=90°(垂直的定义),
∴AD∥EG(同位角相等,两直线平行),
∴∠3=∠E(两直线平行,同位角相等),∠2=∠1(两直线平行,内错角相等).
又∵∠E=∠1(已知),∴∠3=∠2(等量代换),
∴AD平分∠BAC(角平分线的定义).
课堂总结
要判定一个命题是真命题,往往需要从命题的条件出发,根据已知的定义、基本事实、定理(包括推论),一步一步推得结论成立,这样的推理过程叫做证明 。
推 理
推理的过程叫证明
原名、公理
一些条件
+
证明中的每一步推理都要有根据,这些根据可以是已知条件,
也可以是定义、基本事实、定理等.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
1.3.1 证明
浙教版 八年级上册
教学目标
教学目标:
1、了解证明的含义。
2、体验、理解证明的必要性和推理过程中要步步有据。
3、了解证明的表达格式,会按规定格式证明简单命题。
4、通过证明步骤中由命题画出图形,写出已知、求证的过程,继续训练学生由几何语句正确画出几何图形的能力。
重点:证明的含义和表述格式。
难点:按规定格式表述证明的过程。
新知导入
哦……那可
怎么办
【思考】如何证实一个命题是真命题呢?
用我们以前学过的观察,实验,验证特例等方法.
这些方法往往并不可靠.
那已经知道的真命题又是如何证实的
能不能根据已经知道的真命题证实呢
新知讲解
通过观察,先猜想结论,再动手验证:
(1)如图,一组直线a,b,c,d是否都互相平行
a
b
c
d
新知讲解
通过观察,先猜想结论,再动手验证:
(2)当n=0,1,2,3,4时,代数式n -3n+7的值分别是7,5,5,7,11,它们都是质数。那么,命题 “对于自然数n,代数式n -3n+7的值都是素数”是真命题吗
当n=6时, n -3n+7 =25不是素数
新知讲解
要判定一个命题是真命题,往往需要从命题的条件出发,根据已知的定义、基本事实、定理(包括推论),一步一步推得结论成立,这样的推理过程叫做证明 。
推 理
推理的过程叫证明
原名、公理
一些条件
+
新知讲解
例1 已知:如图1-12,DE∥BC,∠1=∠E.
求证:BE平分∠ABC.
证明 ∵DE∥BC(已知),
∴∠2=∠E(两直线平行,内错角相等).
∵∠1=∠E(已知),
∴∠1=∠2,
∴BE平分∠ABC(角平分线的定义).
B
A
D
E
C
1
2
证明过程中的每一步推理都要有依据,依据作为推理的理由,可以写在每一步后的括号内.
新知讲解
例2 已知:如图,AB∥CD,EP,FP分别平分∠BEF,∠DFE.
求证:∠PEF+∠PFE=90°.
A
B
C
D
E
P
F
新知讲解
证明 ∵EP,FP分别平分∠BEF,∠DFE(已知),
∴∠PEF= ∠BEF,∠PFE= ∠DFE(角平分线的定义).
∵AB∥CD(已知),
∴∠BEF+∠DFE=180°(两直线平行,同旁内角互补).
∴∠PEF+∠PFE= ∠BEF+ ∠DFE= (∠BEF+∠DFE)=90°
例2 已知:如图,AB∥CD,EP,FP分别平分∠BEF,∠DFE.
求证:∠PEF+∠PFE=90°.
新知讲解
证明中的每一步推理都要有根据,这些根据可以是已知条件,
也可以是定义、基本事实、定理等.
课堂练习
1.关于证明,下列说法不正确的是( )
A.证明是说明命题是真命题的过程
B.要判定一个命题是真命题常常通过推理的方式
C.要说明一个命题是假命题常采用举反例的方式
D.真命题与假命题都可以通过举反例来说明
D
2.有一条直的宽纸带,按如图所示的方式折叠,则∠α的度数等于( )
A.50° B.60°
C.75° D.85°
C
课堂练习
3.如图,田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是( )
A.垂线段最短
B.经过一点有无数条直线
C.经过两点,有且仅有一条直线
D.两点之间,线段最短
D
4.如图,若AO⊥CO,BO⊥DO,则∠AOB=∠COD,推理的理由是( )
A.同角的补角相等 B.同角的余角相等
C.AO⊥CO D.BO⊥DO
B
∴________∥________
( ).
∴AB∥CD.
课堂练习
5.补充完成下列证明,并填上推理的依据.
已知:如图,AB⊥BC,EF⊥BC,∠1=∠2.
求证:AB∥CD.
证明:∵AB⊥BC,
∴∠ABC=________( ).
90°
垂直的定义
∵EF⊥BC( ),
∴∠FEC=________( ).
∴∠ABC=∠FEC( ).
∴________∥________( ).
∵∠1=∠2,
已知
90°
垂直的定义
等量代换
AB
EF
同位角相等,两直线平行
EF
CD
内错角相等,两直线平行
课堂练习
6.已知:如图,AD⊥BC于D,EG⊥BC于G,∠E=∠1.
求证:AD平分∠BAC.
解:如图,∵AD⊥BC,EG⊥BC(已知),
∴∠4=∠5=90°(垂直的定义),
∴AD∥EG(同位角相等,两直线平行),
∴∠3=∠E(两直线平行,同位角相等),∠2=∠1(两直线平行,内错角相等).
又∵∠E=∠1(已知),∴∠3=∠2(等量代换),
∴AD平分∠BAC(角平分线的定义).
课堂总结
要判定一个命题是真命题,往往需要从命题的条件出发,根据已知的定义、基本事实、定理(包括推论),一步一步推得结论成立,这样的推理过程叫做证明 。
推 理
推理的过程叫证明
原名、公理
一些条件
+
证明中的每一步推理都要有根据,这些根据可以是已知条件,
也可以是定义、基本事实、定理等.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
