1.5.2 用两边夹角关系判定三角形全等 课件(共19张PPT)
文档属性
| 名称 | 1.5.2 用两边夹角关系判定三角形全等 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1022.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-27 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
1.5.2用两边夹角关系判定三角形全等
浙教版 八年级上册
教学目标
教学目标:
1.掌握三角形全等(SAS)的判定方法。
2.掌握线段垂直平分线的性质定理。
3.会运用三角形全等的判定方法、线段的中垂线的性质,解决两条线段相等、两个角相等的问题。
重点:两个三角形全等的判定条件(SAS)。
难点:线段垂直平分线性质定理的证明涉及分类讨论。
新知导入
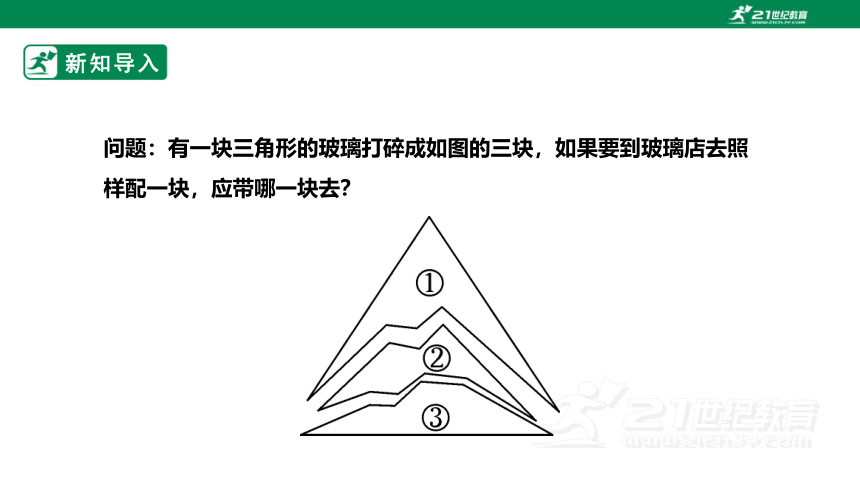
问题:有一块三角形的玻璃打碎成如图的三块,如果要到玻璃店去照样配一块,应带哪一块去?
新知讲解
如图,把两根木条的一端用螺栓固定在一起,木条可自由转动,连结另两端所成的三角形能否唯一确定?
如果固定两木条之间的夹角(即∠BAC)的大小,那么△ABC的形状和大小也随之被确定.
连结另两端所成的三角形不能唯一确定,这就是说,如果两个三角形只有两条边对应相等,那么这两个三角形不一定全等.
例如,图中,△ABC与△AB'C不是全等三角形。
新知讲解
如图,在△ABC和△A'B'C中,∠B=∠B',AB=A'B',BC=B'C'.
△ABC与△A'B'C全等吗?
因为∠B=∠B',当把它们叠在一起时,可以使射线BA与B'A'重合,射线BC与B'C'重合.又因为AB=A'B',BC=B'C',所以点A与点A'重合,点C与点C重合,所以△ABC与△A'B'C重合,
所以△ABC≌△A'B'C.
新知讲解
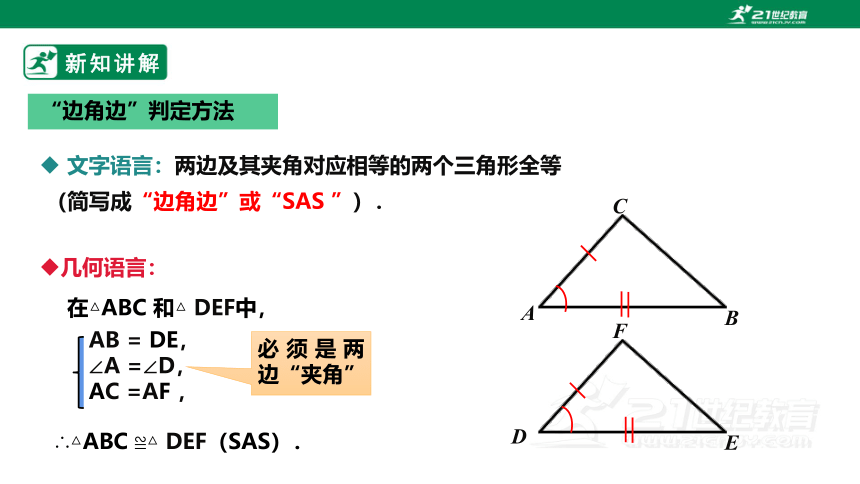
在△ABC 和△ DEF中,
∴△ABC ≌△ DEF(SAS).
文字语言:两边及其夹角对应相等的两个三角形全等
(简写成“边角边”或“SAS ”).
“边角边”判定方法
几何语言:
AB = DE,
∠A =∠D,
AC =AF ,
必须是两边“夹角”
A
B
C
D
E
F
新知讲解
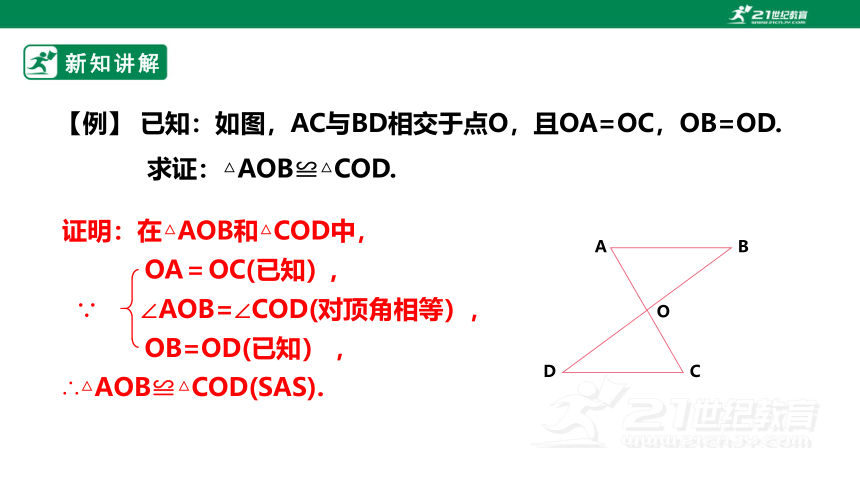
【例】 已知:如图,AC与BD相交于点O,且OA=OC,OB=OD.
求证:△AOB≌△COD.
证明:在△AOB和△COD中,
OA=OC(已知),
∵ ∠AOB=∠COD(对顶角相等),
OB=OD(已知) ,
∴△AOB≌△COD(SAS).
A
B
C
D
O
新知讲解
如图,把两根钢条AA',BB'的中点连在一起,可以做成一个测量工件内槽宽的卡钳.说明卡钳的工作原理。
卡钳的工作原理利用了三角形全等判定定理SAS,
∵O是AA',BB'的中点,
∴AO=A'O,BO=B'O,
又∵∠AOB与∠A'OB'是对顶角,
∴∠AOB=∠A'OB',
∴△AOB≌△A'OB'(SAS),AB=A'B'.
只要量出A'B'的长度,就可以知道工作的内径AB是否符合标准。
新知讲解
垂直于一条线段,并且平分这条线段的直线叫做这条线段的垂直平分线,简称中垂线.
垂直平分线:
A
B
D
l
如图,直线l⊥AB于点D,且AD=BD,直线l就是线段AB的垂直平分线.
新知讲解
在直线l上任意取一点P,用圆规比较点P到点A,B的距离.你发现了什么?
A
B
l
P1
P2
P3
P1A ____P1B
P2A____ P2B
P3A ____P3B
=
=
=
结论:线段垂直平分线上的点到线段两端的距离相等.
能否证明这一结论呢?
新知讲解
已知:如图,直线l⊥AB于点O,且OA=OB.C是直线l上的任意一点.
求证:CA=CB.
C
A
B
l
O
证明 已知OA=OB,当点C与点O为同一点,即重合时,显然CA=CB.
当点C与点O不重合时,
∵直线l⊥AB(已知)
∴∠COA=∠COB=90°(垂直的定义).
新知讲解
证明:在△CAO与△CBO中,
OA=OB(已知),
∵ ∠COA=∠COB,
OC=OC(公共边) ,
∴△CAO≌△CBO(SAS).
∴CA=CB(全等三角形的对应边相等)
已知:如图,直线l⊥AB于点O,且OA=OB.C是直线l上的任意一点.
求证:CA=CB.
C
A
B
l
O
课堂练习
1.如图,已知AB=AE,AC=AD,下列条件中不能判定△ABC≌△AED的是( )
A.BC=ED B.∠BAD=∠EAC
C.∠B=∠E D.∠BAC=∠EAD
C
2.如图,已知AB=AC,AD=AE,若要得到“△ABD≌△ACE”,必须添加一个条件,则下列所添条件不成立的是( )
A.BD=CE B.∠ABD=∠ACE
C.∠BAD=∠CAE D.∠BAC=∠DAE
B
课堂练习
3.如图,在△ABC中,DE是AC的垂直平分线,△ABC的周长为19 cm,△ABD的周长为13 cm,则AE的长为( )
A.3 cm B.6 cm C.12 cm D.16 cm
A
4.【中考·娄底】如图,已知AB=BC,要使△ABD≌ △CBD,还需要加一个条件,你添加的条件是________________.(只需写一个,不添加辅助线)
∠ABD=∠CBD
(答案不唯一)
课堂练习
5.如图,四边形ABCD的对角线AC,BD相交于点O,△ABO≌△ADO.下列结论:
①AC⊥BD;②CB=CD;③△ABC≌△ADC;
④DA=DC.其中所有正确结论的序号是________.
①②③
课堂练习
6.如图,AB与CD相交于点E,AE=CE,DE=BE.求证:∠A=∠C.
课堂总结
1.三角形全等的判定(边角边)
内容
两边及其夹角对应相等的两个三角形全等(简写成 “边角边”或“SAS ”)
应用
为证明线段和角相等提供了新的证法
注意
1.已知两边,必须找“夹角”
2.已知一角和这角的一夹边,必须找这角的另一夹边
2.线段垂直平分线上的点到线段两端的距离相等.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
1.5.2用两边夹角关系判定三角形全等
浙教版 八年级上册
教学目标
教学目标:
1.掌握三角形全等(SAS)的判定方法。
2.掌握线段垂直平分线的性质定理。
3.会运用三角形全等的判定方法、线段的中垂线的性质,解决两条线段相等、两个角相等的问题。
重点:两个三角形全等的判定条件(SAS)。
难点:线段垂直平分线性质定理的证明涉及分类讨论。
新知导入
问题:有一块三角形的玻璃打碎成如图的三块,如果要到玻璃店去照样配一块,应带哪一块去?
新知讲解
如图,把两根木条的一端用螺栓固定在一起,木条可自由转动,连结另两端所成的三角形能否唯一确定?
如果固定两木条之间的夹角(即∠BAC)的大小,那么△ABC的形状和大小也随之被确定.
连结另两端所成的三角形不能唯一确定,这就是说,如果两个三角形只有两条边对应相等,那么这两个三角形不一定全等.
例如,图中,△ABC与△AB'C不是全等三角形。
新知讲解
如图,在△ABC和△A'B'C中,∠B=∠B',AB=A'B',BC=B'C'.
△ABC与△A'B'C全等吗?
因为∠B=∠B',当把它们叠在一起时,可以使射线BA与B'A'重合,射线BC与B'C'重合.又因为AB=A'B',BC=B'C',所以点A与点A'重合,点C与点C重合,所以△ABC与△A'B'C重合,
所以△ABC≌△A'B'C.
新知讲解
在△ABC 和△ DEF中,
∴△ABC ≌△ DEF(SAS).
文字语言:两边及其夹角对应相等的两个三角形全等
(简写成“边角边”或“SAS ”).
“边角边”判定方法
几何语言:
AB = DE,
∠A =∠D,
AC =AF ,
必须是两边“夹角”
A
B
C
D
E
F
新知讲解
【例】 已知:如图,AC与BD相交于点O,且OA=OC,OB=OD.
求证:△AOB≌△COD.
证明:在△AOB和△COD中,
OA=OC(已知),
∵ ∠AOB=∠COD(对顶角相等),
OB=OD(已知) ,
∴△AOB≌△COD(SAS).
A
B
C
D
O
新知讲解
如图,把两根钢条AA',BB'的中点连在一起,可以做成一个测量工件内槽宽的卡钳.说明卡钳的工作原理。
卡钳的工作原理利用了三角形全等判定定理SAS,
∵O是AA',BB'的中点,
∴AO=A'O,BO=B'O,
又∵∠AOB与∠A'OB'是对顶角,
∴∠AOB=∠A'OB',
∴△AOB≌△A'OB'(SAS),AB=A'B'.
只要量出A'B'的长度,就可以知道工作的内径AB是否符合标准。
新知讲解
垂直于一条线段,并且平分这条线段的直线叫做这条线段的垂直平分线,简称中垂线.
垂直平分线:
A
B
D
l
如图,直线l⊥AB于点D,且AD=BD,直线l就是线段AB的垂直平分线.
新知讲解
在直线l上任意取一点P,用圆规比较点P到点A,B的距离.你发现了什么?
A
B
l
P1
P2
P3
P1A ____P1B
P2A____ P2B
P3A ____P3B
=
=
=
结论:线段垂直平分线上的点到线段两端的距离相等.
能否证明这一结论呢?
新知讲解
已知:如图,直线l⊥AB于点O,且OA=OB.C是直线l上的任意一点.
求证:CA=CB.
C
A
B
l
O
证明 已知OA=OB,当点C与点O为同一点,即重合时,显然CA=CB.
当点C与点O不重合时,
∵直线l⊥AB(已知)
∴∠COA=∠COB=90°(垂直的定义).
新知讲解
证明:在△CAO与△CBO中,
OA=OB(已知),
∵ ∠COA=∠COB,
OC=OC(公共边) ,
∴△CAO≌△CBO(SAS).
∴CA=CB(全等三角形的对应边相等)
已知:如图,直线l⊥AB于点O,且OA=OB.C是直线l上的任意一点.
求证:CA=CB.
C
A
B
l
O
课堂练习
1.如图,已知AB=AE,AC=AD,下列条件中不能判定△ABC≌△AED的是( )
A.BC=ED B.∠BAD=∠EAC
C.∠B=∠E D.∠BAC=∠EAD
C
2.如图,已知AB=AC,AD=AE,若要得到“△ABD≌△ACE”,必须添加一个条件,则下列所添条件不成立的是( )
A.BD=CE B.∠ABD=∠ACE
C.∠BAD=∠CAE D.∠BAC=∠DAE
B
课堂练习
3.如图,在△ABC中,DE是AC的垂直平分线,△ABC的周长为19 cm,△ABD的周长为13 cm,则AE的长为( )
A.3 cm B.6 cm C.12 cm D.16 cm
A
4.【中考·娄底】如图,已知AB=BC,要使△ABD≌ △CBD,还需要加一个条件,你添加的条件是________________.(只需写一个,不添加辅助线)
∠ABD=∠CBD
(答案不唯一)
课堂练习
5.如图,四边形ABCD的对角线AC,BD相交于点O,△ABO≌△ADO.下列结论:
①AC⊥BD;②CB=CD;③△ABC≌△ADC;
④DA=DC.其中所有正确结论的序号是________.
①②③
课堂练习
6.如图,AB与CD相交于点E,AE=CE,DE=BE.求证:∠A=∠C.
课堂总结
1.三角形全等的判定(边角边)
内容
两边及其夹角对应相等的两个三角形全等(简写成 “边角边”或“SAS ”)
应用
为证明线段和角相等提供了新的证法
注意
1.已知两边,必须找“夹角”
2.已知一角和这角的一夹边,必须找这角的另一夹边
2.线段垂直平分线上的点到线段两端的距离相等.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
