1.6 尺规作图 课件(共28张PPT)
文档属性
| 名称 | 1.6 尺规作图 课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 941.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-27 10:17:10 | ||
图片预览





文档简介
(共28张PPT)
1.6 尺规作图
浙教版 八年级上册
教学目标
教学目标:
1.了解尺规作图的含义和基本尺规作图的范围.
2.会用直尺和圆规作一个角等于已知角.
3.会用直尺和圆规作三角形:已知三边作三角形,已知两边及其夹角作三角形;已知两角及其一边作三角形.
重点:基本尺规作图:作一个角等于已知角,作已知线段的垂直平分线。
难点:作一个角等于已知角,作已知线段的垂直平分线的做法分析过程有一定的难度,是本节教学的难点。
新知导入
我们已经学习过用直尺和圆规作一条线段等于已知线段及作一个角的平分线.
一起来回忆一下是怎样做的吧!
复习回顾
(3)在射线AC 上截取AB =a ,则线段
AB 就是所要画的线段.
(1)先画射线AC;
(2)用圆规量出线段a的长;
作法:
A
C
B
已知:线段a,求作一条线段等于a.
a
a
复习回顾
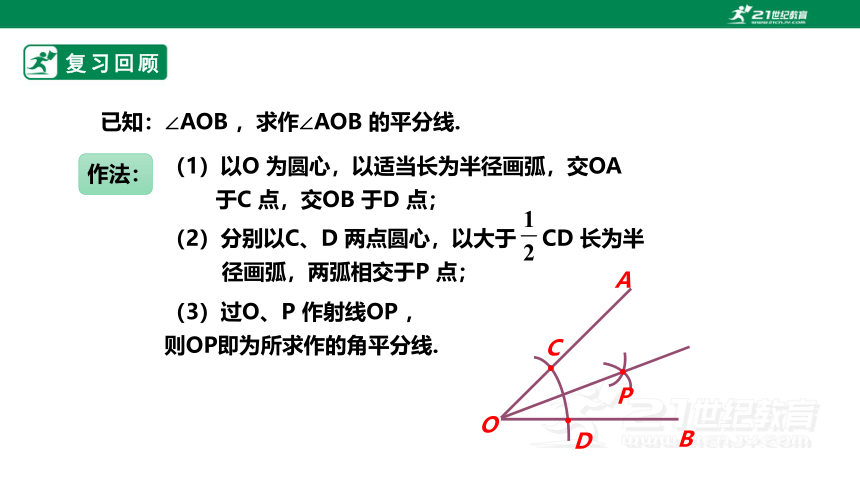
已知:∠AOB ,求作∠AOB 的平分线.
O
B
A
P
C
D
(1)以O 为圆心,以适当长为半径画弧,交OA
于C 点,交OB 于D 点;
(3)过O、P 作射线OP ,
则OP即为所求作的角平分线.
(2)分别以C、D 两点圆心,以大于 CD 长为半
径画弧,两弧相交于P 点;
作法:
新知讲解
在几何作图中,我们把用没有刻度的直尺和圆规作图,
简称尺规作图。
新知讲解
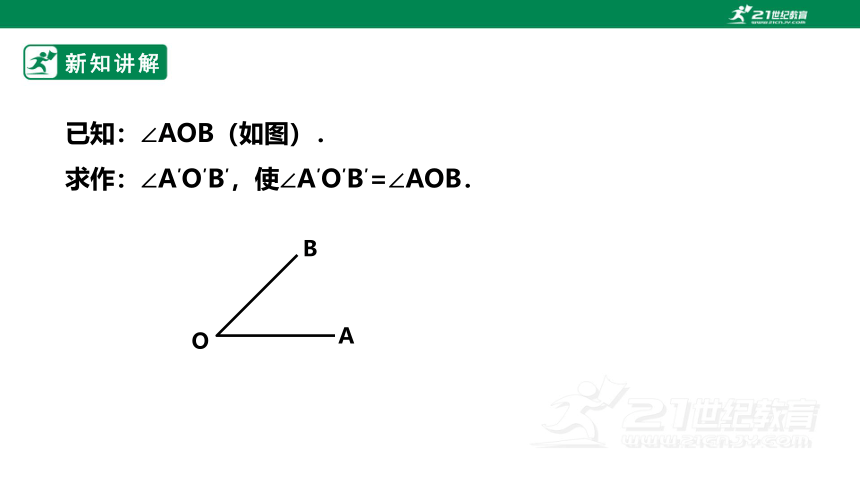
已知:∠AOB(如图).
求作:∠A′O′B′,使∠A′O′B′=∠AOB.
B
O
A
新知讲解
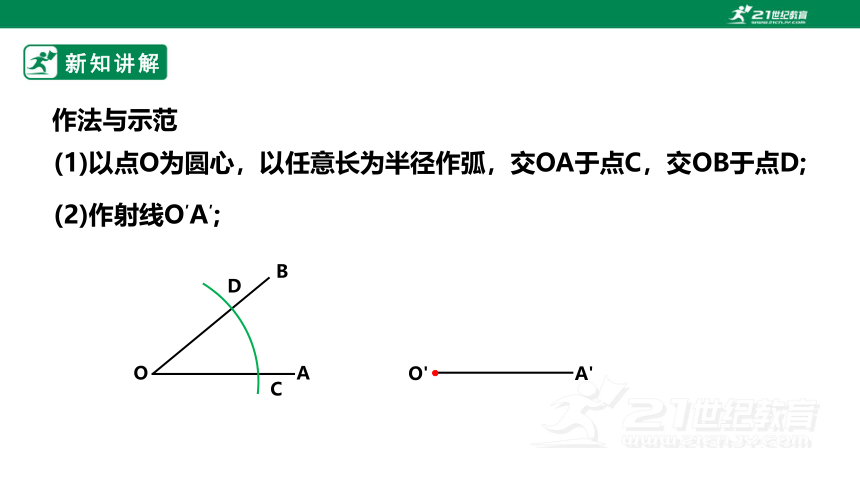
(2)作射线O′A′;
作法与示范
(1)以点O为圆心,以任意长为半径作弧,交OA于点C,交OB于点D;
O
B
A
C
D
O'
A'
新知讲解
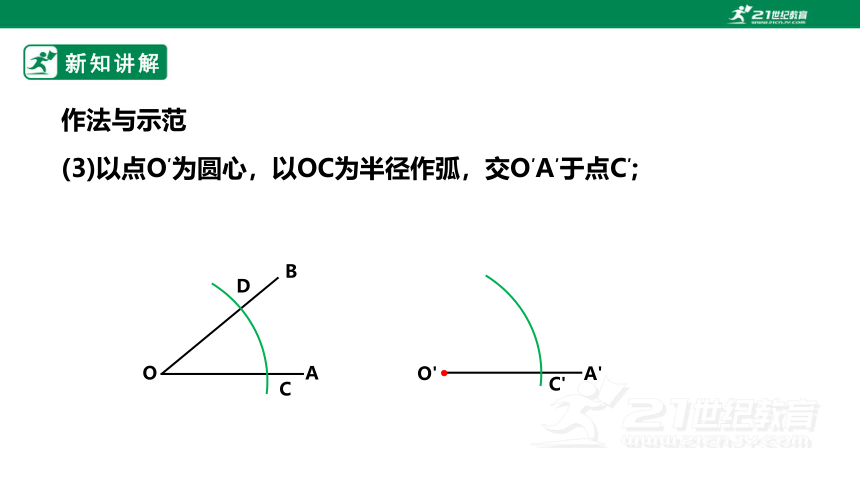
(3)以点O′为圆心,以OC为半径作弧,交O′A′于点C′;
作法与示范
O
B
A
C
D
O'
A'
C'
新知讲解
(4) 以点C′ 为圆心,以CD长为半径作弧,交前面的弧于点D′ ;
(5) 过点O′,D′ 作射线O′ B′ .
作法与示范
O
B
A
C
D
O'
A'
C'
D'
B'
∠A′ O′ B′ 就是所求作的角.
新知讲解
事实上,如图1和图2,连结CD,C'D'.
在△OCD与△O'C'D’中,∵ OC=O'C', OD=O'D', CD=C'D',
∴△OCD≌△O'C'D'(SSS).
∴∠A'O'B'=∠AOB.
O
B
A
C
D
O'
A'
C'
D'
B'
图1
图2
新知讲解
例2 已知线段AB,用直尺和圆规作线段AB的垂直平分线.
A
B
分析 要作线段AB的垂直平分线,只需找出线段AB的垂直平分线上的两个点,这由线段垂直平分线上的点的性质不难找出.
新知讲解
C
D
1.分别以点A和B为圆心,以大于 AB的长为半径作弧,两弧相交于点C和D.
A
B
新知讲解
2.作直线CD.
直线CD就是线段AB的垂直平分线.
注意:以点A和B为圆心画弧时,半径长必须要大于 AB,这样才能得到C,D两个交点.
C
D
A
B
新知讲解
你能根据作法证明直线CD就是线段AB的垂直平分线吗?
已知:如图,连接AC、BC、AD、BD,AC=AD=BC=BD.
求证:CD⊥AB,CD平分AB.
A
B
C
D
1
2
证明:设CD与AB交于点E.
∵在△ACD和△BCD中,
AC=BC
AD=BD
CD=CD
∴△ACD≌△BCD(SSS).
∴∠1=∠2.
∵AC=BC,
∴△ACB是等腰三角形.
∴CE⊥AB,AE=BE.
即 CD⊥AB,CD平分AB.
新知讲解
例3.已知三角形的两角及其夹边,求作这个三角形.
已知:∠α,∠β,线段a(如图).
用直尺和圆规作△ABC,使∠A=∠α,∠B=∠β,AB=a.
请按照给出的作法作出相应的图形.
a
新知讲解
(1)作一条线段AB=a;
(2)分别以A,B为顶点,在AB的同侧作∠DAB=∠α,∠EBA=∠β,DA与EB相交于点C。
D
A
B
作法与示范
新知讲解
作法与示范
D
A
B
E
C
(1)作一条线段AB=a;
(2)分别以A,B为顶点,在AB的同侧作作∠DAB=∠α,∠EBA=∠β,DA与EB相交于点C。
△ABC就是求所作的三角形。
新知讲解
已知:线段a, b, ∠α ,求作:△ABC,使BC= a,AB= b, ∠ABC =∠α
a
b
a
D
E
1.作∠MBN= ∠α
3.连接AC
则△ABC为所求作的三角形
作法:
B
M
D′
E′
N
C
A
已知三角形的两边及其夹角,求作三角形
新知讲解
已知:线段a , b , c,求作:△ABC,使BC=a, AC=b , AB=c
a
b
c
(1)做线段BC=a,
(2)以C为圆心, b为半径画弧
(3)以B为圆心, C为半径画弧,两弧相交于点A
(4)连接AB,AC
则△ABC为所求作的三角形
作法:
B
M
A
C
已知三角形的三条边,求作三角形
新知讲解
常用的作图语言:
(1)过点×、×作线段或射线、直线;
(2)连结两点×、×;
(3)在线段或射线×上截取××=××;
(4)以点×为圆心,以××的长为半径作圆(或画弧),交××于点×;
(5)分别以点×,点×为圆心,以××,××的长为半径作弧,两弧相交于点×;
(6)延长××到点×,使××=××.
课堂练习
1.如图,用尺规作出∠OBF=∠AOB,作图痕迹是( )
A.以点B为圆心,OD为半径的弧
B.以点B为圆心,DC为半径的弧
C.以点E为圆心,OD为半径的弧
D.以点E为圆心,DC为半径的弧
D
2.下列尺规作图,能判断AD是△ABC边上的高的是( )
B
课堂练习
3.如图,下列四种基本尺规作图分别表示:①作一个角等于已知角;②作一个角的平分线;③作一条线段的垂直平分线;④过直线外一点P作已知直线的垂线.对应选项中作法错误的是( )
A.① B.② C.③ D.④
C
课堂练习
4.如图,在△ABC中,AB>AC.按以下步骤作图:分别以B和C为圆心,大于BC一半的长为半径作圆弧,两弧相交于点M和点N;作直线MN交AB于点D;连结CD.若AB=6,AC=4,则△ACD的周长为________.
10
课堂练习
5.尺规作图.(不写作法,保留作图痕迹)已知线段a和∠AOB,点M在OB上,如图所示.
(1)在OA边上作点P,使OP=2a;
(2)作∠AOB的平分线;
(3)过点M作OB的垂线.
解: (1)如图,点P为所求作.
(2)如图,OC为所求作.
(3)如图,MD为所求作.
课堂总结
1.了解尺规作图的含义
2.画一个角等于已知角;
3.作已知线段的垂直平分线;
4.给定边角条件下,求作三角形
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
1.6 尺规作图
浙教版 八年级上册
教学目标
教学目标:
1.了解尺规作图的含义和基本尺规作图的范围.
2.会用直尺和圆规作一个角等于已知角.
3.会用直尺和圆规作三角形:已知三边作三角形,已知两边及其夹角作三角形;已知两角及其一边作三角形.
重点:基本尺规作图:作一个角等于已知角,作已知线段的垂直平分线。
难点:作一个角等于已知角,作已知线段的垂直平分线的做法分析过程有一定的难度,是本节教学的难点。
新知导入
我们已经学习过用直尺和圆规作一条线段等于已知线段及作一个角的平分线.
一起来回忆一下是怎样做的吧!
复习回顾
(3)在射线AC 上截取AB =a ,则线段
AB 就是所要画的线段.
(1)先画射线AC;
(2)用圆规量出线段a的长;
作法:
A
C
B
已知:线段a,求作一条线段等于a.
a
a
复习回顾
已知:∠AOB ,求作∠AOB 的平分线.
O
B
A
P
C
D
(1)以O 为圆心,以适当长为半径画弧,交OA
于C 点,交OB 于D 点;
(3)过O、P 作射线OP ,
则OP即为所求作的角平分线.
(2)分别以C、D 两点圆心,以大于 CD 长为半
径画弧,两弧相交于P 点;
作法:
新知讲解
在几何作图中,我们把用没有刻度的直尺和圆规作图,
简称尺规作图。
新知讲解
已知:∠AOB(如图).
求作:∠A′O′B′,使∠A′O′B′=∠AOB.
B
O
A
新知讲解
(2)作射线O′A′;
作法与示范
(1)以点O为圆心,以任意长为半径作弧,交OA于点C,交OB于点D;
O
B
A
C
D
O'
A'
新知讲解
(3)以点O′为圆心,以OC为半径作弧,交O′A′于点C′;
作法与示范
O
B
A
C
D
O'
A'
C'
新知讲解
(4) 以点C′ 为圆心,以CD长为半径作弧,交前面的弧于点D′ ;
(5) 过点O′,D′ 作射线O′ B′ .
作法与示范
O
B
A
C
D
O'
A'
C'
D'
B'
∠A′ O′ B′ 就是所求作的角.
新知讲解
事实上,如图1和图2,连结CD,C'D'.
在△OCD与△O'C'D’中,∵ OC=O'C', OD=O'D', CD=C'D',
∴△OCD≌△O'C'D'(SSS).
∴∠A'O'B'=∠AOB.
O
B
A
C
D
O'
A'
C'
D'
B'
图1
图2
新知讲解
例2 已知线段AB,用直尺和圆规作线段AB的垂直平分线.
A
B
分析 要作线段AB的垂直平分线,只需找出线段AB的垂直平分线上的两个点,这由线段垂直平分线上的点的性质不难找出.
新知讲解
C
D
1.分别以点A和B为圆心,以大于 AB的长为半径作弧,两弧相交于点C和D.
A
B
新知讲解
2.作直线CD.
直线CD就是线段AB的垂直平分线.
注意:以点A和B为圆心画弧时,半径长必须要大于 AB,这样才能得到C,D两个交点.
C
D
A
B
新知讲解
你能根据作法证明直线CD就是线段AB的垂直平分线吗?
已知:如图,连接AC、BC、AD、BD,AC=AD=BC=BD.
求证:CD⊥AB,CD平分AB.
A
B
C
D
1
2
证明:设CD与AB交于点E.
∵在△ACD和△BCD中,
AC=BC
AD=BD
CD=CD
∴△ACD≌△BCD(SSS).
∴∠1=∠2.
∵AC=BC,
∴△ACB是等腰三角形.
∴CE⊥AB,AE=BE.
即 CD⊥AB,CD平分AB.
新知讲解
例3.已知三角形的两角及其夹边,求作这个三角形.
已知:∠α,∠β,线段a(如图).
用直尺和圆规作△ABC,使∠A=∠α,∠B=∠β,AB=a.
请按照给出的作法作出相应的图形.
a
新知讲解
(1)作一条线段AB=a;
(2)分别以A,B为顶点,在AB的同侧作∠DAB=∠α,∠EBA=∠β,DA与EB相交于点C。
D
A
B
作法与示范
新知讲解
作法与示范
D
A
B
E
C
(1)作一条线段AB=a;
(2)分别以A,B为顶点,在AB的同侧作作∠DAB=∠α,∠EBA=∠β,DA与EB相交于点C。
△ABC就是求所作的三角形。
新知讲解
已知:线段a, b, ∠α ,求作:△ABC,使BC= a,AB= b, ∠ABC =∠α
a
b
a
D
E
1.作∠MBN= ∠α
3.连接AC
则△ABC为所求作的三角形
作法:
B
M
D′
E′
N
C
A
已知三角形的两边及其夹角,求作三角形
新知讲解
已知:线段a , b , c,求作:△ABC,使BC=a, AC=b , AB=c
a
b
c
(1)做线段BC=a,
(2)以C为圆心, b为半径画弧
(3)以B为圆心, C为半径画弧,两弧相交于点A
(4)连接AB,AC
则△ABC为所求作的三角形
作法:
B
M
A
C
已知三角形的三条边,求作三角形
新知讲解
常用的作图语言:
(1)过点×、×作线段或射线、直线;
(2)连结两点×、×;
(3)在线段或射线×上截取××=××;
(4)以点×为圆心,以××的长为半径作圆(或画弧),交××于点×;
(5)分别以点×,点×为圆心,以××,××的长为半径作弧,两弧相交于点×;
(6)延长××到点×,使××=××.
课堂练习
1.如图,用尺规作出∠OBF=∠AOB,作图痕迹是( )
A.以点B为圆心,OD为半径的弧
B.以点B为圆心,DC为半径的弧
C.以点E为圆心,OD为半径的弧
D.以点E为圆心,DC为半径的弧
D
2.下列尺规作图,能判断AD是△ABC边上的高的是( )
B
课堂练习
3.如图,下列四种基本尺规作图分别表示:①作一个角等于已知角;②作一个角的平分线;③作一条线段的垂直平分线;④过直线外一点P作已知直线的垂线.对应选项中作法错误的是( )
A.① B.② C.③ D.④
C
课堂练习
4.如图,在△ABC中,AB>AC.按以下步骤作图:分别以B和C为圆心,大于BC一半的长为半径作圆弧,两弧相交于点M和点N;作直线MN交AB于点D;连结CD.若AB=6,AC=4,则△ACD的周长为________.
10
课堂练习
5.尺规作图.(不写作法,保留作图痕迹)已知线段a和∠AOB,点M在OB上,如图所示.
(1)在OA边上作点P,使OP=2a;
(2)作∠AOB的平分线;
(3)过点M作OB的垂线.
解: (1)如图,点P为所求作.
(2)如图,OC为所求作.
(3)如图,MD为所求作.
课堂总结
1.了解尺规作图的含义
2.画一个角等于已知角;
3.作已知线段的垂直平分线;
4.给定边角条件下,求作三角形
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
