2.7.2 勾股定理逆定理 课件(共18张PPT)
文档属性
| 名称 | 2.7.2 勾股定理逆定理 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 880.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-27 10:26:55 | ||
图片预览






文档简介
(共18张PPT)
2.7.2 勾股定理逆定理
浙教版 八年级上册
教学目标
教学目标:
1.掌握勾股定理的逆定理的内容及应用。
2.会运用勾股定理的逆定理来判断一个三角形是不是直角三角形。
学习重点:探索勾股定理的逆定理。
学习难点:根据勾股定理的逆定理,判断已知三边的三角形是否为直角三角形。
新知导入
命题 如果直角三角形两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
条件:直角三角形的两直角边长为a,b,斜边长为c .
这个命题的条件和结论分别是什么?
结论:a2+b2=c2.
如果将条件和结论反过来,这个命题还成立吗?
新知讲解
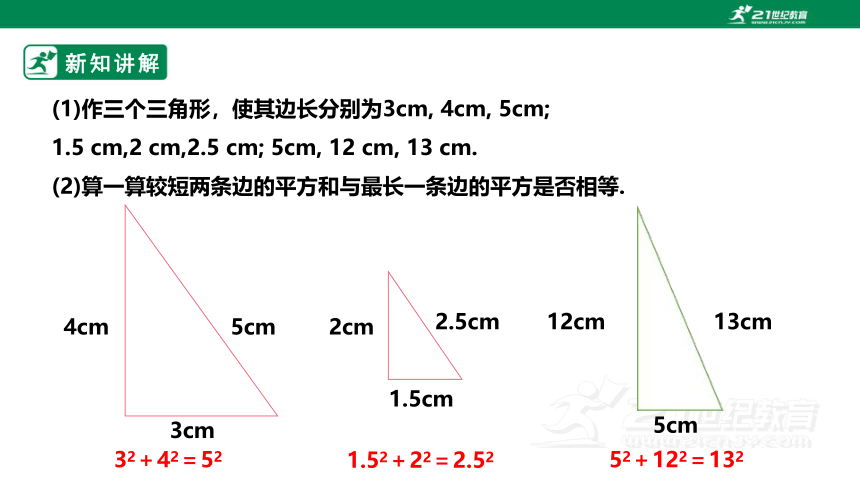
(1)作三个三角形,使其边长分别为3cm, 4cm, 5cm;
1.5 cm,2 cm,2.5 cm; 5cm, 12 cm, 13 cm.
(2)算一算较短两条边的平方和与最长一条边的平方是否相等.
3cm
4cm
5cm
5cm
12cm
13cm
2.5cm
1.5cm
2cm
32+42=52
1.52+22=2.52
52+122=132
新知讲解
(3)量一量所作每一个三角形最大边所对角的度数.
可以用量角器测量,所画的四个三角形都是直角三角形。
由此你得到怎样的猜想?用命题的形式表述你的猜想.
如果三角形的三边长a,b,c满足a2+b2=c2 ,那么这个三角形是直角三角形。
你能证明你的猜想吗?
新知讲解
证明:作Rt△DEF,使∠E=90°,DE=b ,EF=a
在Rt△DEF中,DF2=ED2+EF2=a2+b2
∵c2 =a2 + b2 ,∴DF =c
∴DF=AB,DE=AC ,EF=BC
∴Rt△DFE≌Rt△ABC (SSS)
∴∠C=∠E=90°
已知:在△ABC中,AB=c,AC=b,BC=a ,若c2 =a2+b2
求证:∠C=90°
E
F
D
新知讲解
如果三角形中 有两边的平方和 等于 第三边的平方 ,那么这个三角形是直角三角形.
∵
△ABC是直角三角形
a
b
c
最长边所对的角是直角
较短两边的平方和
最长边的平方
勾股定理的逆定理
新知讲解
勾股定理的逆定理除可以判断三角形是不是直角三角形外,
还可以间接地判断三角形是锐角三角形,还是钝角三角形.
如:已知c是最长边,若a2+b2>c2,则△ABC是锐角三角形;
若a2+b2新知讲解
例3 根据下列条件,分别判断以a,b,c为边的三角形是不是直角三角形.
(1) a=7, b=24, c=25; (2) ,b=1,
解 (1)∵ 72+242=252,∴以7,24,25 为边的三角形是直角三角形.
(2) 也就是较小两边的平方和不等于较大边的平方,∴a,b,c中任何两边的平方和都不等于第三边的平方,
∴以 为边的三角形不是直角三角形.
新知讲解
例4 已知△ABC的三条边长分别为a,b,c,且 a=m2-n2,b=2mn,
c=m2+n2(m>n,m,n 是正整数).△ABC是直角三角形吗 请证明你的判断.
解 △ABC是直角三角形.证明如下:
∵a=m2-n2,b=2mn,c=m2+n2(m>n,m,n 是正整数)
∴a2+b2=(m2-n2)2+(2mn)2=m4-2m2n2+n4+4m2n2
=m4+2m2n2+n4=(m2+n2)2=c2.
∴△ABC是直角三角形(勾股定理的逆定理).
新知讲解
运用勾股定理的逆定理判定直角三角形的一般步骤:
1、先求各边的平方
2、观察较短两边的平方和 与最长边的平方
3、判断是否相等
课堂练习
1.在下列四组数中,不是勾股数的一组数是( )
A.a=15,b=8,c=17
B.a=9,b=12,c=15
C.a=7,b=24,c=25
D.a=3,b=5,c=7
D
2.已知△ABC的三边长分别为5,12,13,则△ABC的面积为( )
A.30 B.60 C.78 D.80
A
课堂练习
3.已知a,b,c为△ABC的三边,若满足(a-b)(a2+b2-c2)=0,则△ABC是( )
A.等边三角形 B.直角三角形
C.等腰直角三角形 D.等腰三角形或直角三角形
D
4.五根小木棒,其长度(单位:cm)分别为8,9,12,15,17,现将它们摆成两个直角三角形,其中正确的是( )
C
问:上述解题过程,从哪一步开始出现错误?
请写出该步的序号:______;
错误的原因为______________________;
本题正确的结论是_________________________________.
课堂练习
5.阅读下面的解题过程:
已知a,b,c为△ABC的三边,且满足a2c2-b2c2=a4-b4,试判断△ABC的形状.
解:∵a2c2-b2c2=a4-b4,①
∴c2(a2-b2)=(a2+b2)(a2-b2),②
∴c2=a2+b2,③
∴△ABC是直角三角形.
③
忽略了a2-b2=0的情况
△ABC是直角三角形或等腰三角形
课堂练习
6.将一根长30 m的细绳折成3段,围成一个三角形,其中的一条边比最短边长7 m,比最长边短1 m,请你判断这个三角形的形状.
解:设这个三角形中中间长度的边长为x m,那么另外两边长分别为(x+1)m,(x-7)m,则x+x+1+x-7=30,解得x=12.
所以这个三角形的三边长分别为5 m,12 m,13 m.
又因为52+122=169=132,所以这个三角形是直角三角形.
课堂总结
如果三角形中两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
勾股定理的逆定理
运用勾股定理的逆定理判定直角三角形的一般步骤:
1、先求各边的平方
2、观察较短两边的平方和 与最长边的平方
3、判断是否相等
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
2.7.2 勾股定理逆定理
浙教版 八年级上册
教学目标
教学目标:
1.掌握勾股定理的逆定理的内容及应用。
2.会运用勾股定理的逆定理来判断一个三角形是不是直角三角形。
学习重点:探索勾股定理的逆定理。
学习难点:根据勾股定理的逆定理,判断已知三边的三角形是否为直角三角形。
新知导入
命题 如果直角三角形两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
条件:直角三角形的两直角边长为a,b,斜边长为c .
这个命题的条件和结论分别是什么?
结论:a2+b2=c2.
如果将条件和结论反过来,这个命题还成立吗?
新知讲解
(1)作三个三角形,使其边长分别为3cm, 4cm, 5cm;
1.5 cm,2 cm,2.5 cm; 5cm, 12 cm, 13 cm.
(2)算一算较短两条边的平方和与最长一条边的平方是否相等.
3cm
4cm
5cm
5cm
12cm
13cm
2.5cm
1.5cm
2cm
32+42=52
1.52+22=2.52
52+122=132
新知讲解
(3)量一量所作每一个三角形最大边所对角的度数.
可以用量角器测量,所画的四个三角形都是直角三角形。
由此你得到怎样的猜想?用命题的形式表述你的猜想.
如果三角形的三边长a,b,c满足a2+b2=c2 ,那么这个三角形是直角三角形。
你能证明你的猜想吗?
新知讲解
证明:作Rt△DEF,使∠E=90°,DE=b ,EF=a
在Rt△DEF中,DF2=ED2+EF2=a2+b2
∵c2 =a2 + b2 ,∴DF =c
∴DF=AB,DE=AC ,EF=BC
∴Rt△DFE≌Rt△ABC (SSS)
∴∠C=∠E=90°
已知:在△ABC中,AB=c,AC=b,BC=a ,若c2 =a2+b2
求证:∠C=90°
E
F
D
新知讲解
如果三角形中 有两边的平方和 等于 第三边的平方 ,那么这个三角形是直角三角形.
∵
△ABC是直角三角形
a
b
c
最长边所对的角是直角
较短两边的平方和
最长边的平方
勾股定理的逆定理
新知讲解
勾股定理的逆定理除可以判断三角形是不是直角三角形外,
还可以间接地判断三角形是锐角三角形,还是钝角三角形.
如:已知c是最长边,若a2+b2>c2,则△ABC是锐角三角形;
若a2+b2
例3 根据下列条件,分别判断以a,b,c为边的三角形是不是直角三角形.
(1) a=7, b=24, c=25; (2) ,b=1,
解 (1)∵ 72+242=252,∴以7,24,25 为边的三角形是直角三角形.
(2) 也就是较小两边的平方和不等于较大边的平方,∴a,b,c中任何两边的平方和都不等于第三边的平方,
∴以 为边的三角形不是直角三角形.
新知讲解
例4 已知△ABC的三条边长分别为a,b,c,且 a=m2-n2,b=2mn,
c=m2+n2(m>n,m,n 是正整数).△ABC是直角三角形吗 请证明你的判断.
解 △ABC是直角三角形.证明如下:
∵a=m2-n2,b=2mn,c=m2+n2(m>n,m,n 是正整数)
∴a2+b2=(m2-n2)2+(2mn)2=m4-2m2n2+n4+4m2n2
=m4+2m2n2+n4=(m2+n2)2=c2.
∴△ABC是直角三角形(勾股定理的逆定理).
新知讲解
运用勾股定理的逆定理判定直角三角形的一般步骤:
1、先求各边的平方
2、观察较短两边的平方和 与最长边的平方
3、判断是否相等
课堂练习
1.在下列四组数中,不是勾股数的一组数是( )
A.a=15,b=8,c=17
B.a=9,b=12,c=15
C.a=7,b=24,c=25
D.a=3,b=5,c=7
D
2.已知△ABC的三边长分别为5,12,13,则△ABC的面积为( )
A.30 B.60 C.78 D.80
A
课堂练习
3.已知a,b,c为△ABC的三边,若满足(a-b)(a2+b2-c2)=0,则△ABC是( )
A.等边三角形 B.直角三角形
C.等腰直角三角形 D.等腰三角形或直角三角形
D
4.五根小木棒,其长度(单位:cm)分别为8,9,12,15,17,现将它们摆成两个直角三角形,其中正确的是( )
C
问:上述解题过程,从哪一步开始出现错误?
请写出该步的序号:______;
错误的原因为______________________;
本题正确的结论是_________________________________.
课堂练习
5.阅读下面的解题过程:
已知a,b,c为△ABC的三边,且满足a2c2-b2c2=a4-b4,试判断△ABC的形状.
解:∵a2c2-b2c2=a4-b4,①
∴c2(a2-b2)=(a2+b2)(a2-b2),②
∴c2=a2+b2,③
∴△ABC是直角三角形.
③
忽略了a2-b2=0的情况
△ABC是直角三角形或等腰三角形
课堂练习
6.将一根长30 m的细绳折成3段,围成一个三角形,其中的一条边比最短边长7 m,比最长边短1 m,请你判断这个三角形的形状.
解:设这个三角形中中间长度的边长为x m,那么另外两边长分别为(x+1)m,(x-7)m,则x+x+1+x-7=30,解得x=12.
所以这个三角形的三边长分别为5 m,12 m,13 m.
又因为52+122=169=132,所以这个三角形是直角三角形.
课堂总结
如果三角形中两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
勾股定理的逆定理
运用勾股定理的逆定理判定直角三角形的一般步骤:
1、先求各边的平方
2、观察较短两边的平方和 与最长边的平方
3、判断是否相等
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
