2.8 直角三角形全等的判定 课件(共25张PPT)
文档属性
| 名称 | 2.8 直角三角形全等的判定 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 948.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-27 10:27:42 | ||
图片预览




文档简介
(共25张PPT)
2.8直角三角形全等的判定
浙教版 八年级上册
教学目标
教学目标:
1.探索两个直角三角形全等的条件.
2.掌握两个直角三角形全等的判定定理(HL).
3.了解角平分线的性质定理的逆定理:角的内部,到角两边距离相等的点,在这个角的平分线上.
学习重点:直角三角形全等的判定方法。
学习难点:运用全等直角三角形的判定方法解决问题。
新知导入
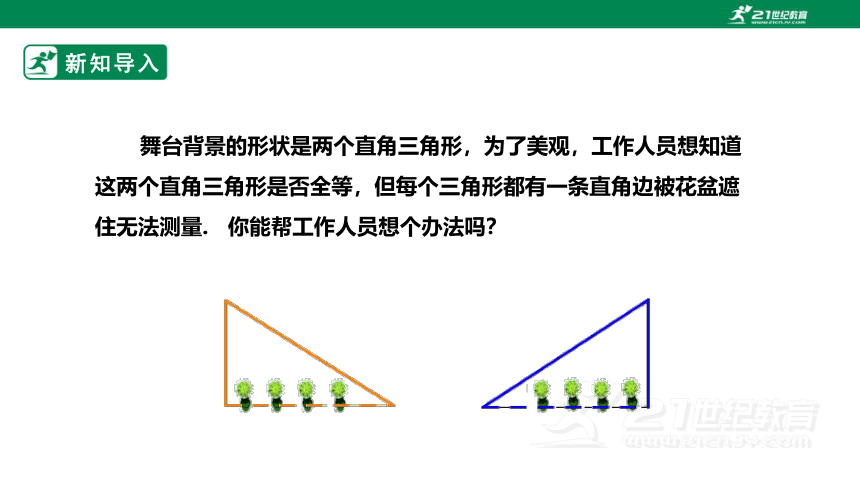
舞台背景的形状是两个直角三角形,为了美观,工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量. 你能帮工作人员想个办法吗?
新知导入
我们已经学过的判定三角形全等的方法有哪些?
定义:能够重合的两个三角形是全等三角形
判定条件1:三边对应相等的两个三角形全等.
(简写为“边边边”或“SSS”)
判定条件2:两边及其夹角对应相等的两个三角形全等
(简写成“边角边”或“SAS ”).
判定条件3:有两角和它们夹边对应相等的两个三角形全等(简写成“角边角”或“ASA”).
判定条件4:两角和其中一角的对边对应相等的两个三角形全等.
(简写成“角角边”或“AAS”).
新知讲解
探究:
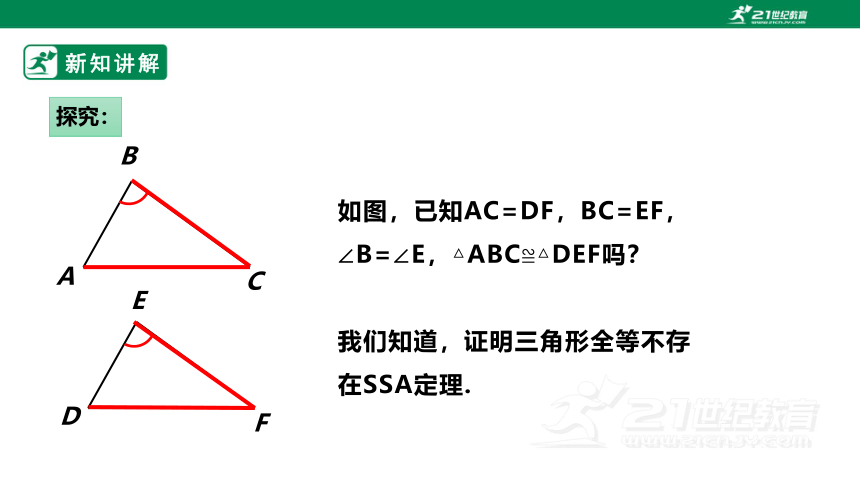
如图,已知AC=DF,BC=EF,
∠B=∠E,△ABC≌△DEF吗?
我们知道,证明三角形全等不存
在SSA定理.
A
B
C
D
E
F
新知讲解
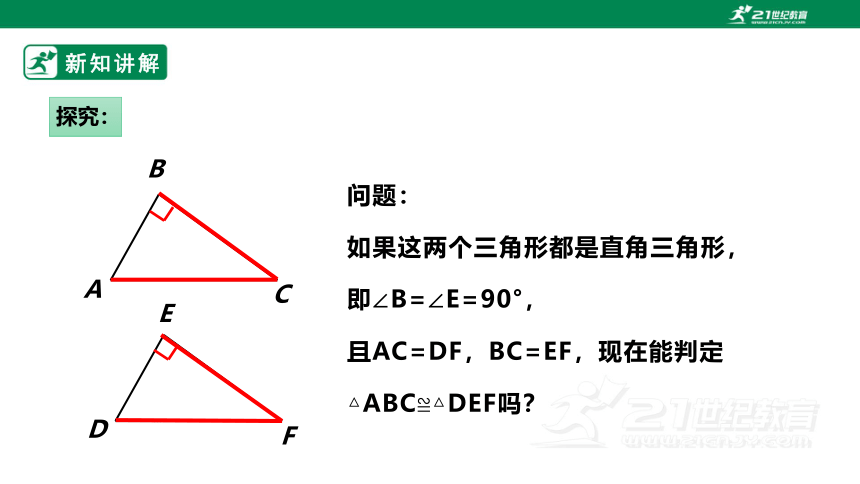
问题:
如果这两个三角形都是直角三角形,
即∠B=∠E=90°,
且AC=DF,BC=EF,现在能判定
△ABC≌△DEF吗?
A
B
C
D
E
F
探究:
新知讲解
问题:任意画一个Rt△ABC,使∠C =90°,再画一个Rt△A′B′C′,使∠C′=90°,B′C′=BC,A′B′=AB,然后把画好的Rt△A′B′C′剪下来放到Rt△ABC上,你发现了什么?
新知讲解
A
B
C
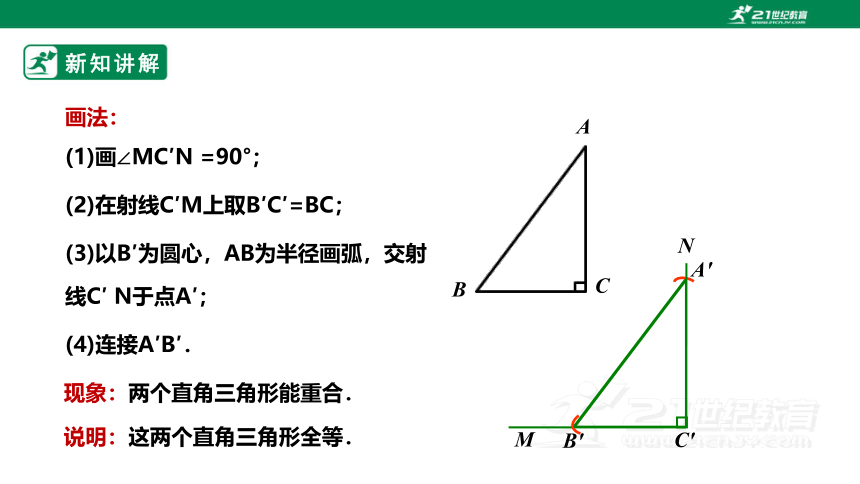
(1)画∠MC′N =90°;
(2)在射线C′M上取B′C′=BC;
(3)以B′为圆心,AB为半径画弧,交射线C′ N于点A′;
(4)连接A′B′.
现象:两个直角三角形能重合.
说明:这两个直角三角形全等.
画法:
A′
N
M
C′
B′
新知讲解
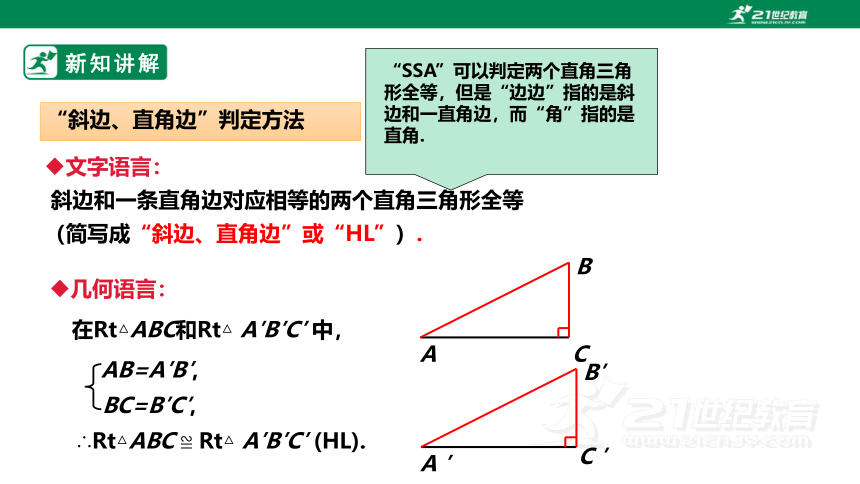
“斜边、直角边”判定方法
文字语言:
斜边和一条直角边对应相等的两个直角三角形全等
(简写成“斜边、直角边”或“HL”).
几何语言:
A
B
C
A ′
B′
C ′
在Rt△ABC和Rt△ A′B′C′ 中,
∴Rt△ABC ≌ Rt△ A′B′C′ (HL).
“SSA”可以判定两个直角三角形全等,但是“边边”指的是斜边和一直角边,而“角”指的是直角.
AB=A′B′,
BC=B′C′,
新知讲解
下面我们给出证明.
已知:如图,在△ACB 和△A'C'B'中,∠C=∠C'=Rt∠,
AB=A'B',AC=A'C'.
求证:Rt△ABC≌Rt△A'B'C'.
A
B
C
A'
B'
C'
新知讲解
证明 如图,延长BC至D. 使 CD=B'C',连结AD.
∵AC=A'C'(已知),∠ACD=Rt∠=∠C'
∴△ADC≌△A'B'C'(SAS)
∴AD=A'B'(全等三角形的对应边相等)
∵A'B'=AB(已知),
∴AD=AB.
A
B
C
D
新知讲解
又∵ AC⊥BD,
∴BC=DC(等腰三角形三线合一)
而AC=AC(公共边),
∴△ADC≌△ABC(SSS) ,
∴△ABC≌△A'B'C'.
A
B
C
D
新知讲解
已知线段a、c(a﹤c)画一个Rt△ABC,使∠C=90° ,
一直角边CB=a,斜边AB=c.
a
c
画法:1.画∠MCN=90 °.
3.以B为圆心,c为半径画弧,交射线CN于点A.
4.连结AB
△ABC就是所要画的直角三角形.
M
C
N
a
B
c
A
2.在射线CM上取CB=a.
新知讲解
例 已知:如图,P是∠AOB内一点,PD⊥OA,PE⊥OB,D,E分别是垂足,且PD=PE. 求证:点P在∠AOB的平分线上.
新知讲解
证明 如图,作射线OP.
∵PD⊥OA,PE⊥OB(已知),
∴∠PDO=∠PEO=90°.
又∵OP=OP(公共边),PD=PE(已知),
∴Rt△PDO≌Rt△PEO(HL).
∴∠1=∠2,
即点P在∠AOB的平分线上(角平分线的定义).
1
2
新知讲解
角的内部,到角两边距离相等的点,在这个角的平分线上.
几何语言:
∵DP⊥OA,PE⊥OB,且DP=EP
∴OP平分∠AOB
角平分线性质定理:
由上面例题,我们得到角平分线的又一性质定理:
新知讲解
几何语言:
∵PD⊥OA, PE⊥OB ,PD=PE
∴ OP平分∠AOB (或∠1= ∠2)
1
2
角平分线性质定理逆定理:
角的内部,到角两边距离相等的点,在这个角的平分线上。
新知讲解
做一做:已知ΔABC如图,请找出一点P,使它到三边距离都相等.
三角形的内心:三角形三条角平分线的交点,叫做三角形的内心,三角形的内心到三边的距离相等.
课堂练习
1.下列可使两个直角三角形全等的条件是( )
A.一个锐角对应相等 B.两个锐角对应相等
C.一条边对应相等 D.两条边对应相等
D
2.根据下列条件,用尺规不能作出唯一直角三角形的是( )
A.已知两直角边
B.已知两锐角
C.已知一直角边和一锐角
D.已知斜边和一直角边
B
课堂练习
3.到△ABC的三条边距离相等的点是△ABC的( )
A.三条中线的交点 B.三条角平分线的交点
C.三条高的交点 D.以上均不对
B
4.如图,AB⊥AC于点A,BD⊥CD于点D,若AC=DB,则下列结论中不正确的是( )
A.∠A=∠D B.∠ABC=∠DCB
C.OB=OD D.OA=OD
C
课堂练习
5.如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D,E,AD和CE交于点H.请你添加一个适当的条件:____________________________________________,使△AEH≌△CEB.
AH=CB(或EH=EB或AE=CE)
6.如图,BE⊥AC,CF⊥AB,垂足分别是E,F.若BE=CF,则图中全等三角形有________对.
3
课堂练习
7.如图,已知AE⊥AB于A,BC⊥AB于B,AE=AB,ED=AC.
求证:ED⊥AC.
又∵在Rt△ABC中,∠CBA=90°,∴∠CAB+∠C=90°.
∴∠CAB+∠EDA=90°.
∴∠AFD=90°.
∴ED⊥AC.
课堂总结
直角三角形的判定方法
斜边和一条直角边对应相等的两个直角三角形全等
(简写成“斜边、直角边”或“HL”).
角的内部,到角两边距离相等的点,在这个角的平分线上.
角平分线性质定理:
角平分线性质定理逆定理:
角的内部,到角两边距离相等的点,在这个角的平分线上。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
2.8直角三角形全等的判定
浙教版 八年级上册
教学目标
教学目标:
1.探索两个直角三角形全等的条件.
2.掌握两个直角三角形全等的判定定理(HL).
3.了解角平分线的性质定理的逆定理:角的内部,到角两边距离相等的点,在这个角的平分线上.
学习重点:直角三角形全等的判定方法。
学习难点:运用全等直角三角形的判定方法解决问题。
新知导入
舞台背景的形状是两个直角三角形,为了美观,工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量. 你能帮工作人员想个办法吗?
新知导入
我们已经学过的判定三角形全等的方法有哪些?
定义:能够重合的两个三角形是全等三角形
判定条件1:三边对应相等的两个三角形全等.
(简写为“边边边”或“SSS”)
判定条件2:两边及其夹角对应相等的两个三角形全等
(简写成“边角边”或“SAS ”).
判定条件3:有两角和它们夹边对应相等的两个三角形全等(简写成“角边角”或“ASA”).
判定条件4:两角和其中一角的对边对应相等的两个三角形全等.
(简写成“角角边”或“AAS”).
新知讲解
探究:
如图,已知AC=DF,BC=EF,
∠B=∠E,△ABC≌△DEF吗?
我们知道,证明三角形全等不存
在SSA定理.
A
B
C
D
E
F
新知讲解
问题:
如果这两个三角形都是直角三角形,
即∠B=∠E=90°,
且AC=DF,BC=EF,现在能判定
△ABC≌△DEF吗?
A
B
C
D
E
F
探究:
新知讲解
问题:任意画一个Rt△ABC,使∠C =90°,再画一个Rt△A′B′C′,使∠C′=90°,B′C′=BC,A′B′=AB,然后把画好的Rt△A′B′C′剪下来放到Rt△ABC上,你发现了什么?
新知讲解
A
B
C
(1)画∠MC′N =90°;
(2)在射线C′M上取B′C′=BC;
(3)以B′为圆心,AB为半径画弧,交射线C′ N于点A′;
(4)连接A′B′.
现象:两个直角三角形能重合.
说明:这两个直角三角形全等.
画法:
A′
N
M
C′
B′
新知讲解
“斜边、直角边”判定方法
文字语言:
斜边和一条直角边对应相等的两个直角三角形全等
(简写成“斜边、直角边”或“HL”).
几何语言:
A
B
C
A ′
B′
C ′
在Rt△ABC和Rt△ A′B′C′ 中,
∴Rt△ABC ≌ Rt△ A′B′C′ (HL).
“SSA”可以判定两个直角三角形全等,但是“边边”指的是斜边和一直角边,而“角”指的是直角.
AB=A′B′,
BC=B′C′,
新知讲解
下面我们给出证明.
已知:如图,在△ACB 和△A'C'B'中,∠C=∠C'=Rt∠,
AB=A'B',AC=A'C'.
求证:Rt△ABC≌Rt△A'B'C'.
A
B
C
A'
B'
C'
新知讲解
证明 如图,延长BC至D. 使 CD=B'C',连结AD.
∵AC=A'C'(已知),∠ACD=Rt∠=∠C'
∴△ADC≌△A'B'C'(SAS)
∴AD=A'B'(全等三角形的对应边相等)
∵A'B'=AB(已知),
∴AD=AB.
A
B
C
D
新知讲解
又∵ AC⊥BD,
∴BC=DC(等腰三角形三线合一)
而AC=AC(公共边),
∴△ADC≌△ABC(SSS) ,
∴△ABC≌△A'B'C'.
A
B
C
D
新知讲解
已知线段a、c(a﹤c)画一个Rt△ABC,使∠C=90° ,
一直角边CB=a,斜边AB=c.
a
c
画法:1.画∠MCN=90 °.
3.以B为圆心,c为半径画弧,交射线CN于点A.
4.连结AB
△ABC就是所要画的直角三角形.
M
C
N
a
B
c
A
2.在射线CM上取CB=a.
新知讲解
例 已知:如图,P是∠AOB内一点,PD⊥OA,PE⊥OB,D,E分别是垂足,且PD=PE. 求证:点P在∠AOB的平分线上.
新知讲解
证明 如图,作射线OP.
∵PD⊥OA,PE⊥OB(已知),
∴∠PDO=∠PEO=90°.
又∵OP=OP(公共边),PD=PE(已知),
∴Rt△PDO≌Rt△PEO(HL).
∴∠1=∠2,
即点P在∠AOB的平分线上(角平分线的定义).
1
2
新知讲解
角的内部,到角两边距离相等的点,在这个角的平分线上.
几何语言:
∵DP⊥OA,PE⊥OB,且DP=EP
∴OP平分∠AOB
角平分线性质定理:
由上面例题,我们得到角平分线的又一性质定理:
新知讲解
几何语言:
∵PD⊥OA, PE⊥OB ,PD=PE
∴ OP平分∠AOB (或∠1= ∠2)
1
2
角平分线性质定理逆定理:
角的内部,到角两边距离相等的点,在这个角的平分线上。
新知讲解
做一做:已知ΔABC如图,请找出一点P,使它到三边距离都相等.
三角形的内心:三角形三条角平分线的交点,叫做三角形的内心,三角形的内心到三边的距离相等.
课堂练习
1.下列可使两个直角三角形全等的条件是( )
A.一个锐角对应相等 B.两个锐角对应相等
C.一条边对应相等 D.两条边对应相等
D
2.根据下列条件,用尺规不能作出唯一直角三角形的是( )
A.已知两直角边
B.已知两锐角
C.已知一直角边和一锐角
D.已知斜边和一直角边
B
课堂练习
3.到△ABC的三条边距离相等的点是△ABC的( )
A.三条中线的交点 B.三条角平分线的交点
C.三条高的交点 D.以上均不对
B
4.如图,AB⊥AC于点A,BD⊥CD于点D,若AC=DB,则下列结论中不正确的是( )
A.∠A=∠D B.∠ABC=∠DCB
C.OB=OD D.OA=OD
C
课堂练习
5.如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D,E,AD和CE交于点H.请你添加一个适当的条件:____________________________________________,使△AEH≌△CEB.
AH=CB(或EH=EB或AE=CE)
6.如图,BE⊥AC,CF⊥AB,垂足分别是E,F.若BE=CF,则图中全等三角形有________对.
3
课堂练习
7.如图,已知AE⊥AB于A,BC⊥AB于B,AE=AB,ED=AC.
求证:ED⊥AC.
又∵在Rt△ABC中,∠CBA=90°,∴∠CAB+∠C=90°.
∴∠CAB+∠EDA=90°.
∴∠AFD=90°.
∴ED⊥AC.
课堂总结
直角三角形的判定方法
斜边和一条直角边对应相等的两个直角三角形全等
(简写成“斜边、直角边”或“HL”).
角的内部,到角两边距离相等的点,在这个角的平分线上.
角平分线性质定理:
角平分线性质定理逆定理:
角的内部,到角两边距离相等的点,在这个角的平分线上。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
