第6章特殊平行四边形单元测试卷(无答案)
文档属性
| 名称 | 第6章特殊平行四边形单元测试卷(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 228.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-08-26 00:00:00 | ||
图片预览

文档简介
特殊平行四边形与梯形复习卷
1.正方形具有而菱形不一定具有的性质是( )
A.四条边都相等 B.对角线相等
C.对角线互相垂直平分 D.每条对角线平分一组对角
2.下列说法正确的是( )
A.对角线相等的四边形是矩形 B.有一组邻边相等的矩形是正方形
C.菱形的四条边、四个角都相等 D.三角形一边上的中线等于这边的一半
3.□ABCD的对角线AC、BD相交于点O,下列条件中,不能判定它为菱形的是( )
A.AB=AD B.AC⊥BD C.∠A=∠D D.CA平分∠BCD
4.一条直线将矩形分割成两个多边形(含三角形),若这两个多边形的内角和分别为M和N,则M+N不可能是( )度 A.360 B.540 C.630 D.720
5.如图,矩形ABCD中,AB>AD,AB=a,AN平分∠DAB,DM⊥AN于点M,CN⊥AN于点N.则DM+CN的值为(用含a的代数式表示)( )
A. B. C. D.
6.如图,已知梯形ABCD中,AD∥BC,BE平分∠ABC,BE⊥CD,AD=3,AB=5,则BC的长为( ) A.6 B.7 C.8 D.9
7.如图,矩形的面积为S,顺次连结各边中点得到四边形 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 ),再顺次连结四边形四边中点得到四边形,依此类推,求四边形的面积是( ) A. B. C. D.
8.如图,正方形ABCD和CEFG的边长分别为m、n,那么 AEG的面积的值 ( )
A.与m、n的大小都有关 B.与m、n的大小都无关
C.只与m的大小有关 D.只与n的大小有关
9.如图,在菱形ABCD中,E、F分别在BC、CD上,且△AEF是等边三角形,AE=AB,则∠BAD 的度数是( ) A.95° B.100° C.105° D.120°
10.如果把左图的正方形纸板剪成四块恰好能拼成右图的矩形,则a等于( )
A. B. C. D.
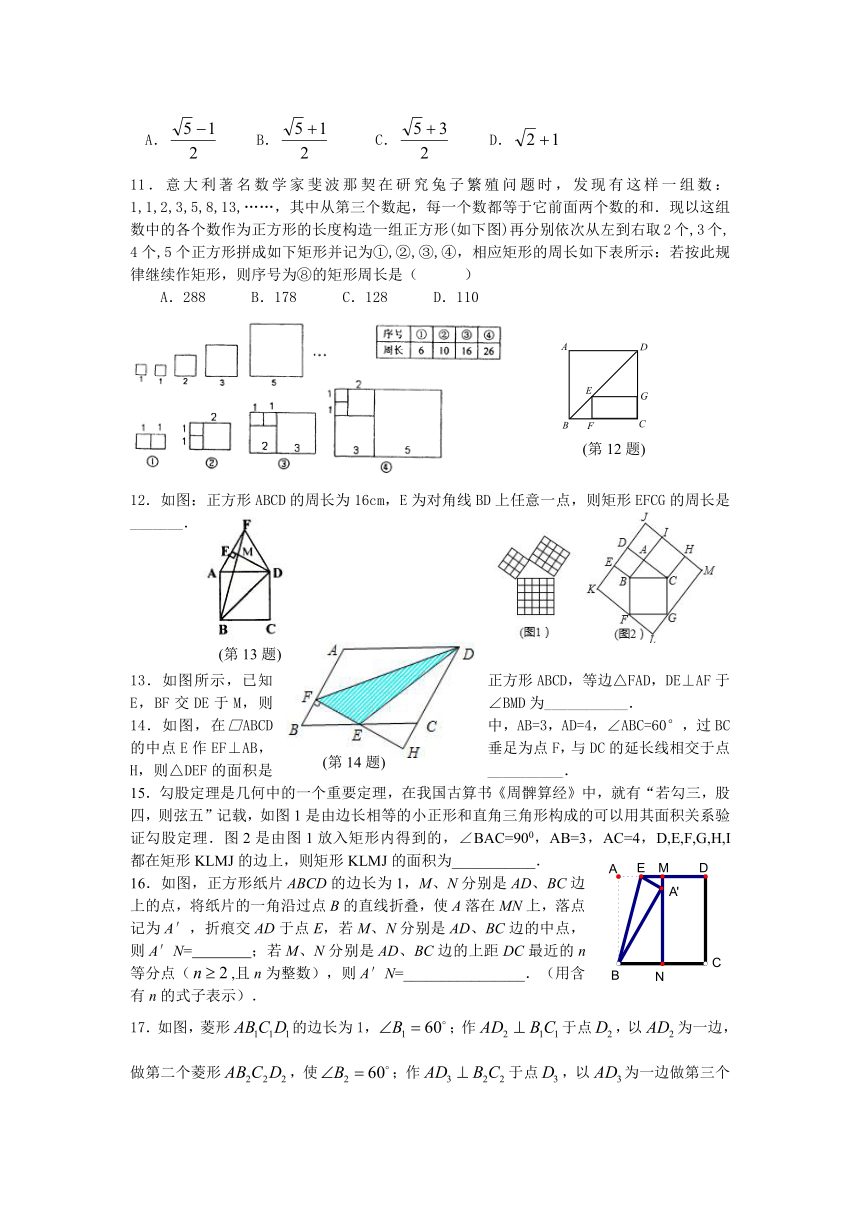
11.意大利著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一组数:1,1,2,3,5,8,13,……,其中从第三个数起,每一个数都等于它前面两个数的和.现以这组数中的各个数作为正方形的长度构造一组正方形(如下图)再分别依次从左到右取2个,3个,
4个,5个正方形拼成如下矩形并记为①,②,③,④,相应矩形的周长如下表所示:若按此规律继续作矩形,则序号为⑧的矩形周长是( )
A.288 B.178 C.128 D.110
12.如图:正方形ABCD的周长为16cm,E为对角线BD上任意一点,则矩形EFCG的周长是_______.
13.如图所示,已知正方形ABCD,等边△FAD,DE⊥AF于E,BF交DE于M,则∠BMD为___________.
14.如图,在□ABCD中,AB=3,AD=4,∠ABC=60°,过BC的中点E作EF⊥AB,垂足为点F,与DC的延长线相交于点H,则△DEF的面积是__________.
15.勾股定理是几何中的一个重要定理,在我国古算书《周髀算经》中,就有“若勾三,股四,则弦五”记载,如图1是由边长相等的小正形和直角三角形构成的可以用其面积关系验证勾股定理.图2是由图1放入矩形内得到的,∠BAC=900,AB=3,AC=4,D,E,F,G,H,I都在矩形KLMJ的边上,则矩形KLMJ的面积为___________.
16.如图,正方形纸片ABCD的边长为1,M、N分别是AD、BC边上的点,将纸片的一角沿过点B的直线折叠,使A落在MN上,落点记为A′,折痕交AD于点E,若M、N分别是AD、BC边的中点,则A′N= ;若M、N分别是AD、BC边的上距DC最近的n等分点(,且n为整数),则A′N=________________.(用含有n的式子表示).
17.如图,菱形的边长为1,;作于点,以为一边,做第二个菱形,使;作于点,以为一边做第三个菱形,使;依此类推,这样做的第个菱形的边的长是 .
18.已知菱形的边长为x,两条对角线长分别为a和b,且,则该菱形较大的一个内角为____________.
19.按如图所示,把一张边长超过10的正方形纸片剪成5个部分,则中间小正方形(阴影部分)的周长为 .
20.长为1,宽为a的矩形纸片(),如图那样折一下,剪下一个边长等于矩形宽度的正方形(称为第一次操作);再把剩下的矩形如图那样折一下,剪下一个边长等于此时矩形宽度的正方形(称为第二次操作);如此反复操作下去.若在第n此操作后,剩下的矩形为正方形,则操作终止.当n=3时,a的值为__________.
21.阅读材料:
我们经常通过认识一个事物的局部或其特殊类型,来逐步认识这个事物. 比如我们通过学习两类特殊的四边形,即平行四边形和梯形(继续学习它们的特殊类型如矩形、等腰梯形等)来逐步认识四边形.我们对课本里特殊四边形的学习,一般先学习图形的定义,再探索发现其性质和判定方法,然后通过解决简单的问题巩固所学知识。
请解决以下问题:
如图,我们把满足AB=CD、CB=CD且AB≠BC的四边形ABCD叫做“筝形”
写出筝形的两个性质(定义除外);
写出筝形的两个判定方法(定义除外)并选出一个进行证明。
22.如图,在□ABCD中,E、F分别为边AB、CD的中点,BD是对角线,过A点作AG∥DB交CB的延长线于点G.
(1)求证:DE∥BF;
(2)若∠G=90,求证四边形DEBF是菱形.
23.如图,已知中,,以斜边为边向外作正方形,且正方形的对角线交于点,连接.已知 ,,求另一直角边的长.
24.如图,梯形ABCD中,AD∥BC,∠DCB=45°,CD =2,BD⊥CD .过点C作CE⊥AB于E,交对角线BD于F.点G为BC中点,连结EG、AF.
(1)求EG的长;
(2)求证:CF =AB +AF.
25.如图,在正方形ABCD中,点E、F分别是BC、DC边上的点,且AE⊥EF.延长EF交正方形外角平分线CP于点P,
(1)试判断AE与EP的大小关系,并说明理由;
(2)若正方形边长为4,BE=1,则在AB边上是否存在一点M,使得四边形DMEP是平行四边形?若存在,请求出AM的长;若不存在,请说明理由.
26.如图,等腰梯形ABCD中,AD∥BC,AD=AB=CD=2,∠C=600,M是BC的中点.将△MDC绕点M旋转,当MD(即MD′)与AB交于一点E,MC(即MC′)同时与AD交于一点F时,点E,F和点A构成△AEF.试探究△AEF的周长是否存在最小值.如果不存在,请说明理由;如果存在,请计算出△AEF周长的最小值.
(第6题)
(第5题)
(第7题)
(第12题)
(第14题)
(第13题)
1
B33
A
C2
B2
C3
D3
B1
D2
C1
第一次操作
第二次操作
(第20题)
B
C
E
D
A
F
P
1.正方形具有而菱形不一定具有的性质是( )
A.四条边都相等 B.对角线相等
C.对角线互相垂直平分 D.每条对角线平分一组对角
2.下列说法正确的是( )
A.对角线相等的四边形是矩形 B.有一组邻边相等的矩形是正方形
C.菱形的四条边、四个角都相等 D.三角形一边上的中线等于这边的一半
3.□ABCD的对角线AC、BD相交于点O,下列条件中,不能判定它为菱形的是( )
A.AB=AD B.AC⊥BD C.∠A=∠D D.CA平分∠BCD
4.一条直线将矩形分割成两个多边形(含三角形),若这两个多边形的内角和分别为M和N,则M+N不可能是( )度 A.360 B.540 C.630 D.720
5.如图,矩形ABCD中,AB>AD,AB=a,AN平分∠DAB,DM⊥AN于点M,CN⊥AN于点N.则DM+CN的值为(用含a的代数式表示)( )
A. B. C. D.
6.如图,已知梯形ABCD中,AD∥BC,BE平分∠ABC,BE⊥CD,AD=3,AB=5,则BC的长为( ) A.6 B.7 C.8 D.9
7.如图,矩形的面积为S,顺次连结各边中点得到四边形 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 ),再顺次连结四边形四边中点得到四边形,依此类推,求四边形的面积是( ) A. B. C. D.
8.如图,正方形ABCD和CEFG的边长分别为m、n,那么 AEG的面积的值 ( )
A.与m、n的大小都有关 B.与m、n的大小都无关
C.只与m的大小有关 D.只与n的大小有关
9.如图,在菱形ABCD中,E、F分别在BC、CD上,且△AEF是等边三角形,AE=AB,则∠BAD 的度数是( ) A.95° B.100° C.105° D.120°
10.如果把左图的正方形纸板剪成四块恰好能拼成右图的矩形,则a等于( )
A. B. C. D.
11.意大利著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一组数:1,1,2,3,5,8,13,……,其中从第三个数起,每一个数都等于它前面两个数的和.现以这组数中的各个数作为正方形的长度构造一组正方形(如下图)再分别依次从左到右取2个,3个,
4个,5个正方形拼成如下矩形并记为①,②,③,④,相应矩形的周长如下表所示:若按此规律继续作矩形,则序号为⑧的矩形周长是( )
A.288 B.178 C.128 D.110
12.如图:正方形ABCD的周长为16cm,E为对角线BD上任意一点,则矩形EFCG的周长是_______.
13.如图所示,已知正方形ABCD,等边△FAD,DE⊥AF于E,BF交DE于M,则∠BMD为___________.
14.如图,在□ABCD中,AB=3,AD=4,∠ABC=60°,过BC的中点E作EF⊥AB,垂足为点F,与DC的延长线相交于点H,则△DEF的面积是__________.
15.勾股定理是几何中的一个重要定理,在我国古算书《周髀算经》中,就有“若勾三,股四,则弦五”记载,如图1是由边长相等的小正形和直角三角形构成的可以用其面积关系验证勾股定理.图2是由图1放入矩形内得到的,∠BAC=900,AB=3,AC=4,D,E,F,G,H,I都在矩形KLMJ的边上,则矩形KLMJ的面积为___________.
16.如图,正方形纸片ABCD的边长为1,M、N分别是AD、BC边上的点,将纸片的一角沿过点B的直线折叠,使A落在MN上,落点记为A′,折痕交AD于点E,若M、N分别是AD、BC边的中点,则A′N= ;若M、N分别是AD、BC边的上距DC最近的n等分点(,且n为整数),则A′N=________________.(用含有n的式子表示).
17.如图,菱形的边长为1,;作于点,以为一边,做第二个菱形,使;作于点,以为一边做第三个菱形,使;依此类推,这样做的第个菱形的边的长是 .
18.已知菱形的边长为x,两条对角线长分别为a和b,且,则该菱形较大的一个内角为____________.
19.按如图所示,把一张边长超过10的正方形纸片剪成5个部分,则中间小正方形(阴影部分)的周长为 .
20.长为1,宽为a的矩形纸片(),如图那样折一下,剪下一个边长等于矩形宽度的正方形(称为第一次操作);再把剩下的矩形如图那样折一下,剪下一个边长等于此时矩形宽度的正方形(称为第二次操作);如此反复操作下去.若在第n此操作后,剩下的矩形为正方形,则操作终止.当n=3时,a的值为__________.
21.阅读材料:
我们经常通过认识一个事物的局部或其特殊类型,来逐步认识这个事物. 比如我们通过学习两类特殊的四边形,即平行四边形和梯形(继续学习它们的特殊类型如矩形、等腰梯形等)来逐步认识四边形.我们对课本里特殊四边形的学习,一般先学习图形的定义,再探索发现其性质和判定方法,然后通过解决简单的问题巩固所学知识。
请解决以下问题:
如图,我们把满足AB=CD、CB=CD且AB≠BC的四边形ABCD叫做“筝形”
写出筝形的两个性质(定义除外);
写出筝形的两个判定方法(定义除外)并选出一个进行证明。
22.如图,在□ABCD中,E、F分别为边AB、CD的中点,BD是对角线,过A点作AG∥DB交CB的延长线于点G.
(1)求证:DE∥BF;
(2)若∠G=90,求证四边形DEBF是菱形.
23.如图,已知中,,以斜边为边向外作正方形,且正方形的对角线交于点,连接.已知 ,,求另一直角边的长.
24.如图,梯形ABCD中,AD∥BC,∠DCB=45°,CD =2,BD⊥CD .过点C作CE⊥AB于E,交对角线BD于F.点G为BC中点,连结EG、AF.
(1)求EG的长;
(2)求证:CF =AB +AF.
25.如图,在正方形ABCD中,点E、F分别是BC、DC边上的点,且AE⊥EF.延长EF交正方形外角平分线CP于点P,
(1)试判断AE与EP的大小关系,并说明理由;
(2)若正方形边长为4,BE=1,则在AB边上是否存在一点M,使得四边形DMEP是平行四边形?若存在,请求出AM的长;若不存在,请说明理由.
26.如图,等腰梯形ABCD中,AD∥BC,AD=AB=CD=2,∠C=600,M是BC的中点.将△MDC绕点M旋转,当MD(即MD′)与AB交于一点E,MC(即MC′)同时与AD交于一点F时,点E,F和点A构成△AEF.试探究△AEF的周长是否存在最小值.如果不存在,请说明理由;如果存在,请计算出△AEF周长的最小值.
(第6题)
(第5题)
(第7题)
(第12题)
(第14题)
(第13题)
1
B33
A
C2
B2
C3
D3
B1
D2
C1
第一次操作
第二次操作
(第20题)
B
C
E
D
A
F
P
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
