4.2代数式[上学期]

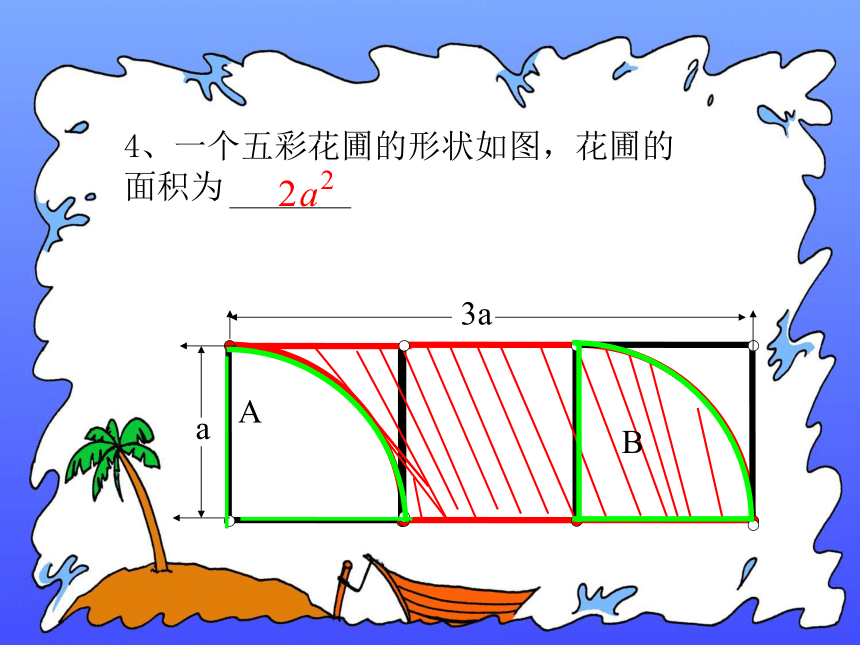
课件17张PPT。课题：4、2 代数式 1、一隧道长 米，一列火车长180米。如果该列火车穿过隧道所花的时间为t分，则列车的速度怎么表示？你能列出速度的算式吗？问题1 什么火车叫做穿过隧道？问题2 火车穿过隧道需经过多少路程？从车头进洞开始到车尾离洞结束。算式为 2、大米的单为a元/千克，食油的单价为b元/千克。买10千克大米、2千克食油共需 元 3、日平均气温是指一天中2：00，8：00，14：00，20：00四个时刻气温的平均值。若上述四个时刻气温的摄氏度数分别是a,b,c,d,则日平均气温的摄氏度数是（10a+2b）4、一个五彩花圃的形状如图，花圃的面积为AB用运算符号把数或表示数的字母连结而成的式子叫做代数式。（这里的运算符号是指加、减、乘、除、乘方、开方）单独一个数或者一个字母也称代数式10a+2b观察上面的四个算式，你能讲出它们是由哪几种运算符号连结而成的吗？例1用代数式表示（1）x的3倍与3的差; （2）x的2倍与y的 的和
（3）a与b的和的平方 （4）2a的立方根解：(1)3x-3(2)2x+ y(3) (a+b)(4)几个注意点：1、系数与字母（或括号）相乘时，如果省略乘号，系数必须写在字母（或括号）的前面。2、带分数与字母（或括号）相乘时，如果省略乘号，带分数要化成假分数。3、结果是商时，一般要写成分数的形式。4、最后结果是和差形式时，如果要写单位，则和或差要先加括号，再写单位。六、课堂练习一1、用代数式表示：
（1）a与b的 的和；
（2）a与b的平方的差；
（3） ， 的和除 s所得的商；
（4）x与1的差的平方根。
(5) m与n的差的平方
（6）a ,b 两数的平方差.
（7） a ,b 两数差的平方.a+ ba-(m-n)2试一试例2 一辆汽车以80千米/时的速度行驶，从A城到B城需t时。如果该车的行驶速度增加v千米/时，那么从A城到B城需多少时间？解： A、B两城间的距离为80t千米，汽车的速度为（80+v）千米/时，此时从A城到B城需 时答：当该车行驶速度增加v千米/时，从A城到B城需 时。问题 你知道A、B两城间的距离是多少千米吗？问题 该车行驶速度增加以后的速度是多少千米/时80t千米（80+v）千米/时想一想、说一说你能帮代数式10x+5y找一些现实生活中的实际情景吗？并解释它表示什么。解释一：火龙果每千克x元，番石榴每千克y元，买10千克火龙果与5千克番石榴共花 元（10x+5y）解释二：火龙果每千克10元，番石榴每千克5元，买x千克火龙果与y千克番石榴共花 元（10x+5y）2、已知甲数比乙数的2倍少1。设乙数为x，用关于x的代数式表示甲数。2x-1据1994年的统计资料：在过去的25年中，大象数量下降了90%。设1994年大象的头数为a，则25 年前的大象头数为多少？解：七、课堂练习二1、用代数式表示：（1）x的2倍与3的和；（2）a的相反数与a的3倍的差；（3）x的3倍与y的4倍的比；（4）a,b,c的平均数2、已知甲数是乙数的倒数的2倍。设乙数为x，用关于x的代数式表示甲数。2x+3-a-3a解：例4 说出下列代数式的意义（1）（a+b)(a-b) (2) (3) (1) a , b 两数的和与a , b 两数的差的积.（2）x ,y 两数的平方和的3倍.（3） x ,y 两数的平方差的一半.5、已知12头大象1天的食品可供1000只老鼠吃600天。假定每头大象和每只老鼠吃的食量分别相等，那么t头大象1天食品可供100只老鼠吃多少天？解 ： 500t答： t头大象1天食品可供100只老鼠吃500t天.4、甲、乙两品牌上3衣的单价分别为x元、 y元。在换季时，甲品牌上衣按4折（即原价的40%）销售，乙品牌上衣按6折销售。这时购买两种品牌的上衣各一件，共需多少元？解 ： 40%x+60%y答：购买两种品牌的上衣各一件，共需（40%x+60%y）元。 问题1 1头大象1天的食品可供1000只老鼠吃几天？问题2 1000只老鼠吃50天的食品给100只老鼠吃几天？50天500天八、小结、反思1、代数式的概念用运算符号把数或表示数的字母连结而成的式子叫做代数式。
单独一个数或者一个字母也称代数式2、写代数式的注意点：谢谢指导！