代数式复习[上学期]

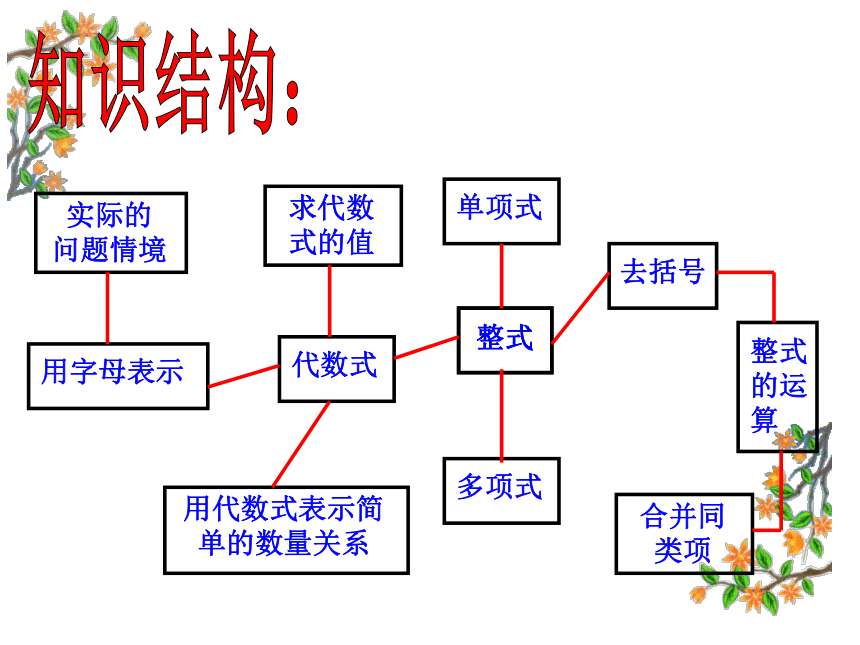
课件22张PPT。1.1从自然数到分数第四章代数式的复习知识结构：1、一个代数式一般由数、表示数的字母
和运算符号组成，这里的运算是指：
、 、 、
、 、 。 单独
的一个数或者一个字母也称代数 式。知识要点：用数代替代数式里的字母，计算后所得的
结果叫做 。加法减法乘法除法乘方开方代数式的值 2、由数与字母或字母与字母相乘组成的代
式叫做 ；单项式中数字因数叫
做这个单项式的 ；所有字母的
指数的和叫做这个单项式的 。 由几个 相加组成的代数式叫做
多项式。在多项式中，每个单项式叫做多项
式的 ；不含字母的项叫做 ；
就是这个多项式的次
数。单项式系数次数单项式项常数项次数最高的项的次数单项式、多项式统称为 。整式 3、多项式中，所含 相同，并且
也相同的项，叫做
同类项。4、主要运算法则：（1）合并同类项法则：把同类项的 相
加，所得的结果作为系数，
不变。（2）去括号法则：括号前面是 “ + ” 号，
把 去掉，括
号里各项 ；字母相同字母的指数系数字母和字母的指数括号和它前面的“+”号都不变号（3）整式的加减运算可归结为 和
。（2）去括号法则：括号前面是 “ - ” 号，
把 去掉，括
号里各项 。去括号的
法则的依据是分配律，即：
a ( b + c ) = 。括号和它前面的“ – ”号都改变符号ab + ac去括号合并同类项例1、用代数式表示：例题分析：（2）某产品的价格是 p 元，其中成本比
其价格少10%，则此产品的成本是
。（1）比 a 的5倍小 8 的数是 。（3）一本书有 m 页，第一天读了全书页数
的 四分之一，第二天读了剩下的三分
之一，则没有读的页数是 。5a - 80.9p? m例2、某校男生人数是女生人数的4倍，女
生人数是教师人数的9倍，设分别用
a、b、c 依次表示男生、女生及教师
人数。
（1）试用含 c 的代数式表示全校师生
的总数。
（2）若 b = 360 ，求该校师生总人数。女生人数为：9c 男生人数为：36c 全校师生总人数为 ：36c + 9c + c = 46c 当 b=360时 c = 40 ，所以 46c = 1840 （人）3、有理数 a、b、c 在数轴上的位置如图所示：试化简：解：由数轴上点的位置可知：
a + c < 0，a + b + c < 0，a – b > 0原式= - ( a +c )+( a+b+c) – ( a – b ) – ( 2b – a ) = - a – c +a+b+c – a +b – 2b +a= 04、已知一个多项式加上 5x2 + 3x – 2 的2倍得
1 – 3x2 + x ，求这个多项式。 解：这个多项式=
（1 – 3x2 + x ）- 2（5x2 + 3x – 2 ）= 1 – 3x2 + x - 10x2 - 6x + 4 = – 13x2 -5x +55、已知代数式 ( 3a2 – ab+2b2 ) – ( a2 – 5ab+b2)
– 2 ( a2 + 2ab +b2 )。 （1）试说明这个代数式的值与 a 的取值
无关； （2）若 b = - 2 ，求这个代数式的值。解：( 1 ) 原式= 3a2 – ab+2b2 –a2 + 5ab -b2
– 2a2 - 4ab - 2b2= – b2 所以，代数式的值与a 的值无关。（2）当 b = - 2 时，原式 = - (-2)2 = - 4 。6、如图是一个数值转换机示意图，请按要求在括号内填写转换步骤，在表格中填写数值。× 3 - 1 ÷ 2 - ? - 2 根据题目要求，列出代数式：
（1)用代数式表示比a的5倍小3的数是 .
(2)用代数式表示：m与n的平方和加上m、n的积的2倍是 .
(3)a的2倍的倒数与b的差用代数式表示
为 .
(4)除以x-1的商是2x的数用代数式表示为 .
(5)每件上衣a元，6件上衣值 元.
(6)一本练习本0.50元，一支圆珠笔1.20元，买x本练习本、y支圆珠笔共需 元5a-3 m2+n2+2mn2x(x-1)6a(0.5x+1.20y)设甲数为x，用代数式表示乙数。
①甲数的2倍比乙数少7 。
②甲乙两数的和为39 。
③甲数的平方比乙数多c 。
④甲数比乙数的2倍大3 。2x+739-x x2-c1.单项式-7x2y3z的系数是 __________,次数是_________;
2.关于x,y的单项式xa+1y2是6次单项式,则a=________;
3.多项式5x3y+3x2y3-4xy-y2+6中,次数最高的项是_3x2y3___,次数最低的项是______,第三项的系数是_______,它是____次_____项式.
4.两个三次多项式的和的次数最多是_________次.
5.多项式ax2-3x+4与多项式4x2+5x+6和不含二次项,则a=___.-7635+6-4五五三-41、当 m = 时，代数式 3xmy与 –2x2 y
是同类项。课内练习：2、若 a – b =10，那么15 – a + b 的值是 。3、若 A – (- 3x ) = x2 + 3x – 1 ，则 A= 。2515 – a + b = 15 – ( a – b ) = 15 – 10 = 5 A= (x2 + 3x – 1) + ( - 3x )= x2 – 1x2 – 15、若 a 是一个有理数，则下列式子中一定
正确的是 （ ）
(A) 10a > a (B) a < a
(C) a > 0 (D) ≥ 04、一列数
按此规律写下去，第n个数是 。D6、填写下表，并观察下列两个代数式的值
的变化情况：(1) n 为何值时，两代数式的值相等？(2) 随着 n 逐渐变大， n2与7n+8 的差如何变
化？181522293643505764101491625364964解： 原式 = a – 2b 当 a = 6 , b = - 2 时

原式 = a – 2b = ×6 – 2 ×( - 2 )=24探索与思考：32、如下边的一排方格中，每一个字母表示
一个数，已知其中任何连续三个方格中
的数之和为 19 ，
求 ( A + B ) – ( C - D ) 的值。同学们 再见！