浙教版数学八上 5.3 一次函数(2) 课件(共19张PPT)
文档属性
| 名称 | 浙教版数学八上 5.3 一次函数(2) 课件(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 551.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-31 17:41:24 | ||
图片预览






文档简介
(共19张PPT)
5.3 一次函数(2)
正比例函数的解析式是什么?
一次函数的解析式是什么?
y=kx
(k为常数,且k≠0)
y=kx+b
(k、b为常数,且k≠0)
当b=0时,
一次函数y=kx+b就变形为正比例函数y=kx
温故知新
例1、已知y是x一次函数,当x=3时, y=1;当x=-2时, y=-14 。
(3)当y=4时自变量x的值;
(2)当x=5时函数y的值;
(1)求这个一次函数的表达式和自变量x的取值范围;
解:(1)设y=kx+b,由已知得
1= 3k+b
-14= -2k+b
解得:k=3,
b=-8
∴这个一次函数的解析式为:y=3x-8 (x为任何实数)
(2)当x=5时,y=15-8=7
(3)当y=4时,3x-8=4 解得x=4
(4)当y>4时,求自变量x的取值范围.
(4)当y>4时,3x-8>4 解得x>4
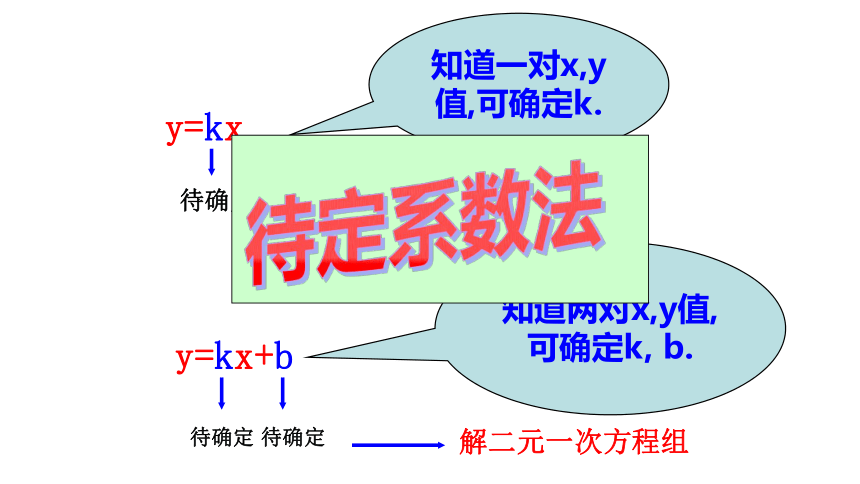
y=kx
y=kx+b
知道一对x,y值,可确定k.
知道两对x,y值,可确定k, b.
待确定
待确定
待确定
解一元一次方程
解二元一次方程组
待定系数法
1、设:所求的一次函数解析式为y=kx+b;
2、列:依已知列出关于k、b的方程组;
3、解:解方程组,求得k、b;
4、写:把k、b的值代入y=kx+b ,写出一次函数解析式。
用待定系数法求一次函数解析式的一般步骤是怎样的呢?
想一想
1.铜的质量M与体积V成正比例,已知当V=5cm3时,M=44.5g,求:
2.已知y是x的一次函数,且当x=-2时,y=7;
当x=3时,y=-8;求这个一次函数的解析式。
如何确定正比例函数和一次函数解析式
完成153页的课内练习
⑵体积为0.3dm3的铜棒的质量.
⑴铜的质量M(g)关于体积V(cm3)的函数解析式,
以及铜的密度p;
3、已知y+m与x-1成正比例,当x=-1时,y=-15 ;当x=7时,y=1。求:
(2)当-3<y<7时,自变量x的取值范围;
(1)y关于x的函数解析式;
解:(1)设y+m=k(x-1),即y=kx-k-m,由已知得:
-k-k-m=-15
7k-k-m=1
解得: k=2,
m=11
∴y关于x的函数解析式是 y=2x-13
(2)当-3<y<7时,即-3<2x-13<7,解得5<x<10
例4 某地区从1995年底开始,沙漠面积几乎每年以相同的速度增长.据有关报道,到2001年底,该地区的沙漠面积已从1998年底的100.6万公顷扩展到101.2万公顷。
①沙漠面积是怎么变化的?
②沙漠面积变化跟什么有关系?
③设95年年底沙漠面积为b万公顷,每经过一年,沙漠面积增加
k万公顷.经过x年,沙漠面积增加到y万公顷.则y 和 x的关系?
y=kx+b
④也就是说可选用一次函数来描述沙漠面积的变化,只要
求出系数k和b.
⑤根据题设条件能否建立关于这两个常数的二元一次方程组
(1)可选用什么数学方法来描述该地区的沙漠面积的变化
(2)如果该地区的沙漠化得不到治理,那么到2020年底,
该地区的沙漠面积将增加到多少公顷
98年年底 沙漠面积100.6万公顷;
01年年底 沙漠面积101.2万公顷
例3 某地区从1995年底开始,沙漠面积几乎每年以相同的速度增长.据有关报道,到2001年底,该地区的沙漠面积已从1998年底的100.6万公顷扩展到101.2万公顷。
(1)可选用什么数学方法来描述该地区的沙漠面积的变化
(2)如果该地区的沙漠化得不到治理,那么到2020年底,
该地区的沙漠面积将增加到多少公顷
解:
(1)设95年年底沙漠面积为b万公顷,每经过一年,沙漠面积增加k万公顷,经过x年,沙漠面积为y万公顷,由题意得 y=kx+b
把x=3时,y=100.6;x=6时,y=101.2分别代入y=kx+b,得
100.6=3k+b
101.2=6k+b
①
②
解得
k=0.2
b=100
∴
y=0.2x+100
(2)当x=25时,y=0.2×25+100=105
答:(略)
1.我们这个问题中反映这两个变量关系的是什么函数?
(一次函数)
所以可设所求的函数解析式为y=kx+b
2.如何求未知的两个常数k和b?
根据题设条件能否建立关于这两个常数的二元一次方程组
3.上述方法就是待定系数法,从而求出函数解析式
很多城市的出租车按里程收费:在一定的里程内按定额
收费(起步价),超出规定里程部分按与超出里程的整
千米数(不足1千米的按1千米计算)成正比例收费。某
市出租车的起步价里程为4km,起步价为10元(不计等
待时间)
练一练1:
课本153页课内练习3
(1)小明一次在该市乘车,从计费表上看到乘车里程和车费分别为6km,14.00元,请用函数解析式表示出租车超出起步价里程时的计费方法;
(2)如果你在该市乘坐出租车的里程为3km,那么需付多少车费?如果乘车里程为8km呢?
按某饮料厂生产一种饮料,经测算,用1吨水生产的饮料所获利润y(元)是1吨水的买入价x(元)的一次函数。根据下表提供的数据,求y关于x的函数解析式;并求当水价为每吨10元时,1吨水生产的饮料所获的利润是多少?
1吨水的买入价(元) 4 6
利润y(元) 200 198
解:
设y=kx+b
当x=4时,y=200;当x=6时,y=198
200=4k+b
198=6k+b
①
②
解得
k=-1
b=204
∴
y=-x+204
∴
作业题3:
练一练2:
课本作业题4
某航空公司规定旅客可免费托运一定质量的行李,超过规定质量的行李需买行李票,行李票费用y(元)是行李质量x(kg)的一次函数。己知当行李的质量分别为20kg,40kg时,需支付的行李票费用为15元和45元,求y与x之间的函数解析式。
y=1.5x-15
令y=0, 则x=10
你能求出旅客最多可免费携带行李多少千克吗?
思考:
练一练3
课本作业题4
按一航空公司规定旅客可免费托运一定质量的行李,超过规定质量的行李需买行李票,行李票费用y(元)是行李质量x(kg)的一次函数。己知当行李的质量分别为20kg,40kg时,需支付的行李票费用为15元和45元,求y与x之间的函数解析式。
练一练3
你能求出旅客最多可免费携带行李多少千克吗?
畅所欲言
这节课我们主要学习了哪些内容
用待定系数法求一次函数的解析式.
作业题5.
已知y+m与x-n成正比例(其中m,n是常数)
(1)y是x的一次函数吗?
(2)如果当y=-15时,x=11;当x=7时,y=1;
求y关于x的函数解析式
新知拓展
解:(1)
设y+m=k(x-n),
(k是常数,且 k≠0)
∴y=kx-kn-m
∵k、m、n都是常数
∴ -kn-m 是常数
∴ y是关于x的一次函数
整体
(2)设y=kx+b, 则
11k+b= -15
7k+b=1
{
∴y=- 4x+29
k =-4
b =29
{
解得
答: y关于x的函数解析
式为
y=-4x+29
∴ y+m=kx-kn
(作业本)某山区的平均气温与该地海拔的关系件下表:
若海拔用x(m)表示,平均气温用y(℃)表示,试写出y关于x的函数解析式;
若某种植物适宜生长在18~20℃(包含18℃和20℃)的山区,请问改植物适宜种植的地段在海拔多少米处?
海拔(m) 0 100 200 300 400 ……
平均气温(℃) 22 21.5 21 20.5 20 ……
作业辅导
(学法)已知一次函数y=kx+b,当x减少5时,y增加3,则k=____
1、爸爸准备为小明买一双新的运动鞋,但要小明自己算出穿几码的鞋.小明回家量了妈妈36码的鞋长23厘米,爸爸41码的鞋子长25.5厘米.你能帮小明算算他穿的21.5厘米长的鞋是几码吗?看看你自己穿的鞋子的码数和长度是否也符合你所发现的规律?
课外拓展:
2、按近几年,我国经济快速发展,电力需求最大,供应不足,某市为了鼓励居民节约用电,对居民用电收费采取了价格浮动政策;每户居民每月用电不超过20度时,每度电费0.5元;超过20度时,超过部分每度电费0.6元。该市民王先生家七月份用电x度。
1)求王先生家应付电费y元与用电量x之间的函数解析式
2)若王先生家该月用电80度,求他需付的电费;
3)若王先生家该月付电费22元,求他家该月的用电量;
课外拓展:
5.3 一次函数(2)
正比例函数的解析式是什么?
一次函数的解析式是什么?
y=kx
(k为常数,且k≠0)
y=kx+b
(k、b为常数,且k≠0)
当b=0时,
一次函数y=kx+b就变形为正比例函数y=kx
温故知新
例1、已知y是x一次函数,当x=3时, y=1;当x=-2时, y=-14 。
(3)当y=4时自变量x的值;
(2)当x=5时函数y的值;
(1)求这个一次函数的表达式和自变量x的取值范围;
解:(1)设y=kx+b,由已知得
1= 3k+b
-14= -2k+b
解得:k=3,
b=-8
∴这个一次函数的解析式为:y=3x-8 (x为任何实数)
(2)当x=5时,y=15-8=7
(3)当y=4时,3x-8=4 解得x=4
(4)当y>4时,求自变量x的取值范围.
(4)当y>4时,3x-8>4 解得x>4
y=kx
y=kx+b
知道一对x,y值,可确定k.
知道两对x,y值,可确定k, b.
待确定
待确定
待确定
解一元一次方程
解二元一次方程组
待定系数法
1、设:所求的一次函数解析式为y=kx+b;
2、列:依已知列出关于k、b的方程组;
3、解:解方程组,求得k、b;
4、写:把k、b的值代入y=kx+b ,写出一次函数解析式。
用待定系数法求一次函数解析式的一般步骤是怎样的呢?
想一想
1.铜的质量M与体积V成正比例,已知当V=5cm3时,M=44.5g,求:
2.已知y是x的一次函数,且当x=-2时,y=7;
当x=3时,y=-8;求这个一次函数的解析式。
如何确定正比例函数和一次函数解析式
完成153页的课内练习
⑵体积为0.3dm3的铜棒的质量.
⑴铜的质量M(g)关于体积V(cm3)的函数解析式,
以及铜的密度p;
3、已知y+m与x-1成正比例,当x=-1时,y=-15 ;当x=7时,y=1。求:
(2)当-3<y<7时,自变量x的取值范围;
(1)y关于x的函数解析式;
解:(1)设y+m=k(x-1),即y=kx-k-m,由已知得:
-k-k-m=-15
7k-k-m=1
解得: k=2,
m=11
∴y关于x的函数解析式是 y=2x-13
(2)当-3<y<7时,即-3<2x-13<7,解得5<x<10
例4 某地区从1995年底开始,沙漠面积几乎每年以相同的速度增长.据有关报道,到2001年底,该地区的沙漠面积已从1998年底的100.6万公顷扩展到101.2万公顷。
①沙漠面积是怎么变化的?
②沙漠面积变化跟什么有关系?
③设95年年底沙漠面积为b万公顷,每经过一年,沙漠面积增加
k万公顷.经过x年,沙漠面积增加到y万公顷.则y 和 x的关系?
y=kx+b
④也就是说可选用一次函数来描述沙漠面积的变化,只要
求出系数k和b.
⑤根据题设条件能否建立关于这两个常数的二元一次方程组
(1)可选用什么数学方法来描述该地区的沙漠面积的变化
(2)如果该地区的沙漠化得不到治理,那么到2020年底,
该地区的沙漠面积将增加到多少公顷
98年年底 沙漠面积100.6万公顷;
01年年底 沙漠面积101.2万公顷
例3 某地区从1995年底开始,沙漠面积几乎每年以相同的速度增长.据有关报道,到2001年底,该地区的沙漠面积已从1998年底的100.6万公顷扩展到101.2万公顷。
(1)可选用什么数学方法来描述该地区的沙漠面积的变化
(2)如果该地区的沙漠化得不到治理,那么到2020年底,
该地区的沙漠面积将增加到多少公顷
解:
(1)设95年年底沙漠面积为b万公顷,每经过一年,沙漠面积增加k万公顷,经过x年,沙漠面积为y万公顷,由题意得 y=kx+b
把x=3时,y=100.6;x=6时,y=101.2分别代入y=kx+b,得
100.6=3k+b
101.2=6k+b
①
②
解得
k=0.2
b=100
∴
y=0.2x+100
(2)当x=25时,y=0.2×25+100=105
答:(略)
1.我们这个问题中反映这两个变量关系的是什么函数?
(一次函数)
所以可设所求的函数解析式为y=kx+b
2.如何求未知的两个常数k和b?
根据题设条件能否建立关于这两个常数的二元一次方程组
3.上述方法就是待定系数法,从而求出函数解析式
很多城市的出租车按里程收费:在一定的里程内按定额
收费(起步价),超出规定里程部分按与超出里程的整
千米数(不足1千米的按1千米计算)成正比例收费。某
市出租车的起步价里程为4km,起步价为10元(不计等
待时间)
练一练1:
课本153页课内练习3
(1)小明一次在该市乘车,从计费表上看到乘车里程和车费分别为6km,14.00元,请用函数解析式表示出租车超出起步价里程时的计费方法;
(2)如果你在该市乘坐出租车的里程为3km,那么需付多少车费?如果乘车里程为8km呢?
按某饮料厂生产一种饮料,经测算,用1吨水生产的饮料所获利润y(元)是1吨水的买入价x(元)的一次函数。根据下表提供的数据,求y关于x的函数解析式;并求当水价为每吨10元时,1吨水生产的饮料所获的利润是多少?
1吨水的买入价(元) 4 6
利润y(元) 200 198
解:
设y=kx+b
当x=4时,y=200;当x=6时,y=198
200=4k+b
198=6k+b
①
②
解得
k=-1
b=204
∴
y=-x+204
∴
作业题3:
练一练2:
课本作业题4
某航空公司规定旅客可免费托运一定质量的行李,超过规定质量的行李需买行李票,行李票费用y(元)是行李质量x(kg)的一次函数。己知当行李的质量分别为20kg,40kg时,需支付的行李票费用为15元和45元,求y与x之间的函数解析式。
y=1.5x-15
令y=0, 则x=10
你能求出旅客最多可免费携带行李多少千克吗?
思考:
练一练3
课本作业题4
按一航空公司规定旅客可免费托运一定质量的行李,超过规定质量的行李需买行李票,行李票费用y(元)是行李质量x(kg)的一次函数。己知当行李的质量分别为20kg,40kg时,需支付的行李票费用为15元和45元,求y与x之间的函数解析式。
练一练3
你能求出旅客最多可免费携带行李多少千克吗?
畅所欲言
这节课我们主要学习了哪些内容
用待定系数法求一次函数的解析式.
作业题5.
已知y+m与x-n成正比例(其中m,n是常数)
(1)y是x的一次函数吗?
(2)如果当y=-15时,x=11;当x=7时,y=1;
求y关于x的函数解析式
新知拓展
解:(1)
设y+m=k(x-n),
(k是常数,且 k≠0)
∴y=kx-kn-m
∵k、m、n都是常数
∴ -kn-m 是常数
∴ y是关于x的一次函数
整体
(2)设y=kx+b, 则
11k+b= -15
7k+b=1
{
∴y=- 4x+29
k =-4
b =29
{
解得
答: y关于x的函数解析
式为
y=-4x+29
∴ y+m=kx-kn
(作业本)某山区的平均气温与该地海拔的关系件下表:
若海拔用x(m)表示,平均气温用y(℃)表示,试写出y关于x的函数解析式;
若某种植物适宜生长在18~20℃(包含18℃和20℃)的山区,请问改植物适宜种植的地段在海拔多少米处?
海拔(m) 0 100 200 300 400 ……
平均气温(℃) 22 21.5 21 20.5 20 ……
作业辅导
(学法)已知一次函数y=kx+b,当x减少5时,y增加3,则k=____
1、爸爸准备为小明买一双新的运动鞋,但要小明自己算出穿几码的鞋.小明回家量了妈妈36码的鞋长23厘米,爸爸41码的鞋子长25.5厘米.你能帮小明算算他穿的21.5厘米长的鞋是几码吗?看看你自己穿的鞋子的码数和长度是否也符合你所发现的规律?
课外拓展:
2、按近几年,我国经济快速发展,电力需求最大,供应不足,某市为了鼓励居民节约用电,对居民用电收费采取了价格浮动政策;每户居民每月用电不超过20度时,每度电费0.5元;超过20度时,超过部分每度电费0.6元。该市民王先生家七月份用电x度。
1)求王先生家应付电费y元与用电量x之间的函数解析式
2)若王先生家该月用电80度,求他需付的电费;
3)若王先生家该月付电费22元,求他家该月的用电量;
课外拓展:
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
