浙教版八年级上册2.1图形的轴对称课件(共26张PPT)
文档属性
| 名称 | 浙教版八年级上册2.1图形的轴对称课件(共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 986.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-02 00:00:00 | ||
图片预览






文档简介
(共26张PPT)
2.1 图形的轴对称
你能从数学的角度说说蝴蝶的特点吗?
如果一个图形沿着一条直线折起来,直线两侧的部分能够相互重合,那么这个图形叫做轴对称图形,这条直线就是它的对称轴。
概念
对称轴两侧能互相重合的两个点叫做对称点。
对于以上各轴对称图形,你能找出对称轴吗?
用对折的方法判断一个图形是不是轴对称图形
1、下列图形是轴对称图形吗?你是怎样判别的?
请你试一试
请你在周围环境中找出轴对称的物体和建筑物.
2.说一说:
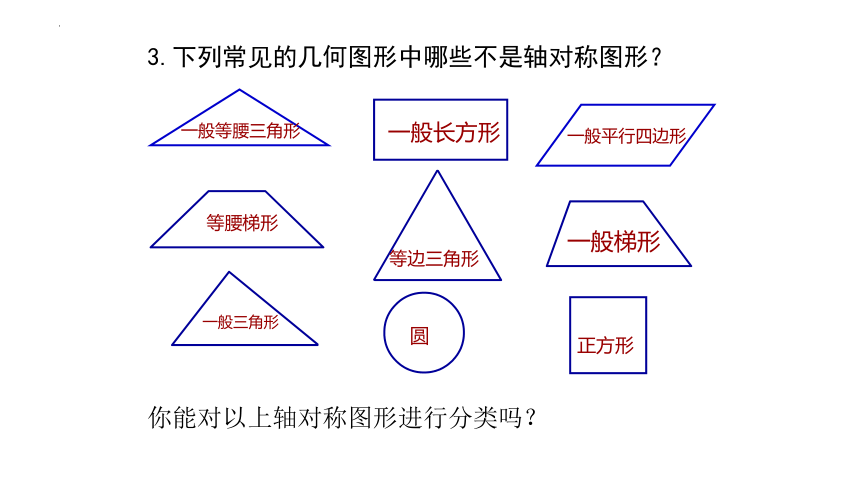
3.下列常见的几何图形中哪些不是轴对称图形?
一般等腰三角形
等腰梯形
正方形
一般长方形
等边三角形
一般三角形
圆
一般梯形
一般平行四边形
你能对以上轴对称图形进行分类吗?
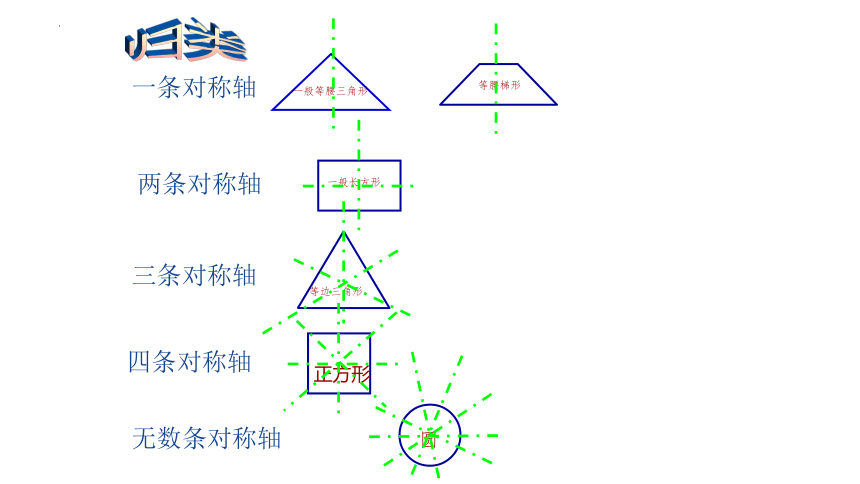
一条对称轴
一般等腰三角形
等腰梯形
两条对称轴
一般长方形
三条对称轴
等边三角形
四条对称轴
正方形
无数条对称轴
圆
归类
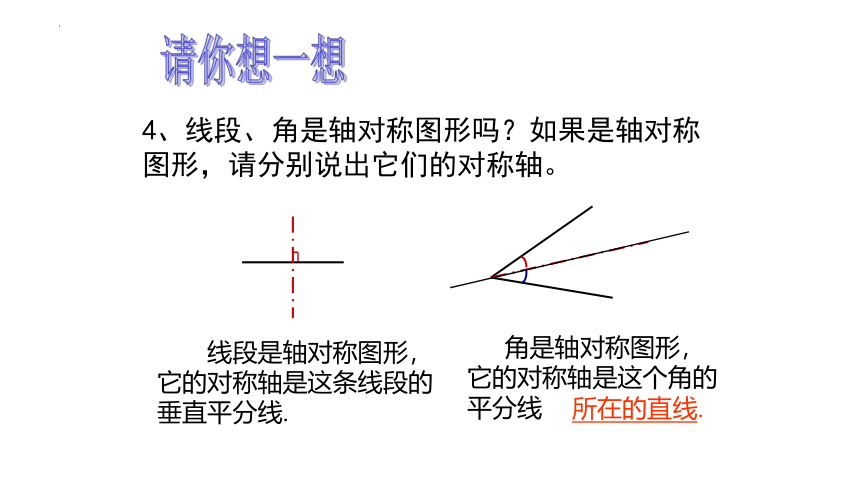
4、线段、角是轴对称图形吗?如果是轴对称图形,请分别说出它们的对称轴。
请你想一想
线段是轴对称图形,它的对称轴是这条线段的垂直平分线.
角是轴对称图形,它的对称轴是这个角的平分线
所在的直线.
5、判断
轴对称图形必有对称轴 ( )
轴对称图形只有一条对称轴 ( )
合作学习:
6、如图,AD平分∠BAC,AB=AC.
(1) 四边形ABCD是轴对称图形吗?
请说出它的对称轴。
哪一点与点B对称?
(2) 连接BC,交AD于点E。把四边形ABDC沿AD对折,BE与CE重合吗? ∠AEC和 ∠AEB 呢?
A
B
C
D
解:∵ AD平分∠BAC
∴ ∠BAD = ∠CAD
E
当沿AD对折时,射线AB与射线AC重合
∵ AB=AC
∴ 点B与点C重合,点E与点E重合
∴ ∠AEC = ∠AEB = 90°
问题:对称轴AD与连结两个对称点之间的线段 BC有什么关系?
∴ BE与CE重合, ∠AEC与∠AEB重合
轴对称图形的性质:
对称轴垂直平分连结两个对称点的线段。
归纳
分别画出下列轴对称图形的对称轴:
解:(1)如图,作线段AB的垂直平分线l ,直线l 就是所求的对称轴。
l
(2)如图,作线段CD的垂直平分线m,直线m就是所求的对称轴。
A
B
m
练习一
作轴对称图形的对称轴,一般步骤是:
第一步:找一组对称点
第二步:画对称点连线
第三步:作连线的中垂线
归纳:
A
A'
∴ 点A′即为所求作的点
M
l
┓
O
练习二
以直线 为对称轴,求A点的对称点。
l
A
B
A'
B'
l
M
N
┓
┓
O
P
练习三
∴线段A′B′即为所求的线段
以直线 为对称轴,求作A、B两点的对称点,并画出连结对称点后的图形。
l
例1、如图,已知△ABC和直线m.以直线m为对称轴,求作以点A,B,C为对称点A ,B ,C 为顶点的△A B C
∴△A′B′C′即为所求的三角形
1、找点
2、作垂线
3、截取等长
4、连结
作图步骤
5、下结论
归纳:
请大家再看看左面两组图形
每一组里,左边的图形沿直线对折后与右边的图形完全重合吗?
由一个图形变为另一个图形,并使这两个图形沿一条直线折叠后能够互相重合,这样的图形改变叫做图形的轴对称。
这条直线就是对称轴。
图形的轴对称性质:
成轴对称的两个图形是全等图形
说明:(1)图形的轴对称是两个图形
(2)折叠
(3)重合
归纳:
轴对称图形和图形的轴对称的区别与联系
轴对称图形
图形的轴对称
区别
联系
图形
(1)轴对称图形是指( )
具有特殊形状的图形,
只对( ) 图形而言;
(2)对称轴( ) 只有一条
(1)轴对称是指( )图形
的位置关系,必须涉及
( )图形;
(2)只有( )对称轴.
如果把轴对称图形沿对称轴
分成两部分,那么这两个图形
就关于这条直线成轴对称.
如果把两个成轴对称的图形
拼在一起看成一个整体,那
么它就是一个轴对称图形.
一个
一个
不一定
两个
两个
一条
共同点
沿一条直线对折,对折的两部分能够完全重合
例2、如图2-8,直线l表示草原上的一条河流。一骑马少年从A地出发,去河边让马饮水,然后返回位于B地的家中。他沿怎样的路线行走,能使路程最短?作出这条最短路线。
解:作点A关于直线 的对称点A‘,连结A’B , 交直线 于点C,连结AC,骑马少年沿折线A-C-B的路线行走时路程最短。
证明:设P是直线 上任意一点,连结AP,A'P.
由作图知,直线 垂直平分AA',
则AC=A'C,AP=A'P(线段垂直平分线上的点到线段两端的距离相等) 。
∴AP+BP=A‘P+BP≧A’B,
A'B=A'C+BC=AC+BC,
即AP+BP≧AC+BC
∴沿折线A-C-B的路线行走时路程最短。
1.如图,AB垂直平分线段CD,垂足为点B,点E、F是AB上的点,CD=40,AB=35,则图中阴影部分的面积是 。
当堂检测
350
A
B
A′
2、如图,EFGH是矩形的台球桌面,有两球分别位于A、B两点的位置,试问怎样撞击A球,才能使A球先碰撞台边EF反弹后再击中B球?
E
F
G
H
解:1.作点A关于EF的对称点A′
2.连结A′B交EF于点C则沿AC撞击黑球A,必沿CB反弹击中白球B。
C
3、如图已知直角三角形ABC。
(1)以直角边AC所在的直线为对称轴,作出与直角三角形ABC成轴对称的图形
(2)第(1)题作出的图形和原图形组成一个等腰三角形吗?请说明理由。
课堂小结
一个概念:
轴对称图形
一个性质:
轴对称图形的性质
对称轴垂直平分连结两个对称点之间的线段。
两种技能:
(1)作轴对称图形的对称轴;
(2)作轴对称图形中已知点的对称点.
应用轴对称图形的性质作图:
2.1 图形的轴对称
你能从数学的角度说说蝴蝶的特点吗?
如果一个图形沿着一条直线折起来,直线两侧的部分能够相互重合,那么这个图形叫做轴对称图形,这条直线就是它的对称轴。
概念
对称轴两侧能互相重合的两个点叫做对称点。
对于以上各轴对称图形,你能找出对称轴吗?
用对折的方法判断一个图形是不是轴对称图形
1、下列图形是轴对称图形吗?你是怎样判别的?
请你试一试
请你在周围环境中找出轴对称的物体和建筑物.
2.说一说:
3.下列常见的几何图形中哪些不是轴对称图形?
一般等腰三角形
等腰梯形
正方形
一般长方形
等边三角形
一般三角形
圆
一般梯形
一般平行四边形
你能对以上轴对称图形进行分类吗?
一条对称轴
一般等腰三角形
等腰梯形
两条对称轴
一般长方形
三条对称轴
等边三角形
四条对称轴
正方形
无数条对称轴
圆
归类
4、线段、角是轴对称图形吗?如果是轴对称图形,请分别说出它们的对称轴。
请你想一想
线段是轴对称图形,它的对称轴是这条线段的垂直平分线.
角是轴对称图形,它的对称轴是这个角的平分线
所在的直线.
5、判断
轴对称图形必有对称轴 ( )
轴对称图形只有一条对称轴 ( )
合作学习:
6、如图,AD平分∠BAC,AB=AC.
(1) 四边形ABCD是轴对称图形吗?
请说出它的对称轴。
哪一点与点B对称?
(2) 连接BC,交AD于点E。把四边形ABDC沿AD对折,BE与CE重合吗? ∠AEC和 ∠AEB 呢?
A
B
C
D
解:∵ AD平分∠BAC
∴ ∠BAD = ∠CAD
E
当沿AD对折时,射线AB与射线AC重合
∵ AB=AC
∴ 点B与点C重合,点E与点E重合
∴ ∠AEC = ∠AEB = 90°
问题:对称轴AD与连结两个对称点之间的线段 BC有什么关系?
∴ BE与CE重合, ∠AEC与∠AEB重合
轴对称图形的性质:
对称轴垂直平分连结两个对称点的线段。
归纳
分别画出下列轴对称图形的对称轴:
解:(1)如图,作线段AB的垂直平分线l ,直线l 就是所求的对称轴。
l
(2)如图,作线段CD的垂直平分线m,直线m就是所求的对称轴。
A
B
m
练习一
作轴对称图形的对称轴,一般步骤是:
第一步:找一组对称点
第二步:画对称点连线
第三步:作连线的中垂线
归纳:
A
A'
∴ 点A′即为所求作的点
M
l
┓
O
练习二
以直线 为对称轴,求A点的对称点。
l
A
B
A'
B'
l
M
N
┓
┓
O
P
练习三
∴线段A′B′即为所求的线段
以直线 为对称轴,求作A、B两点的对称点,并画出连结对称点后的图形。
l
例1、如图,已知△ABC和直线m.以直线m为对称轴,求作以点A,B,C为对称点A ,B ,C 为顶点的△A B C
∴△A′B′C′即为所求的三角形
1、找点
2、作垂线
3、截取等长
4、连结
作图步骤
5、下结论
归纳:
请大家再看看左面两组图形
每一组里,左边的图形沿直线对折后与右边的图形完全重合吗?
由一个图形变为另一个图形,并使这两个图形沿一条直线折叠后能够互相重合,这样的图形改变叫做图形的轴对称。
这条直线就是对称轴。
图形的轴对称性质:
成轴对称的两个图形是全等图形
说明:(1)图形的轴对称是两个图形
(2)折叠
(3)重合
归纳:
轴对称图形和图形的轴对称的区别与联系
轴对称图形
图形的轴对称
区别
联系
图形
(1)轴对称图形是指( )
具有特殊形状的图形,
只对( ) 图形而言;
(2)对称轴( ) 只有一条
(1)轴对称是指( )图形
的位置关系,必须涉及
( )图形;
(2)只有( )对称轴.
如果把轴对称图形沿对称轴
分成两部分,那么这两个图形
就关于这条直线成轴对称.
如果把两个成轴对称的图形
拼在一起看成一个整体,那
么它就是一个轴对称图形.
一个
一个
不一定
两个
两个
一条
共同点
沿一条直线对折,对折的两部分能够完全重合
例2、如图2-8,直线l表示草原上的一条河流。一骑马少年从A地出发,去河边让马饮水,然后返回位于B地的家中。他沿怎样的路线行走,能使路程最短?作出这条最短路线。
解:作点A关于直线 的对称点A‘,连结A’B , 交直线 于点C,连结AC,骑马少年沿折线A-C-B的路线行走时路程最短。
证明:设P是直线 上任意一点,连结AP,A'P.
由作图知,直线 垂直平分AA',
则AC=A'C,AP=A'P(线段垂直平分线上的点到线段两端的距离相等) 。
∴AP+BP=A‘P+BP≧A’B,
A'B=A'C+BC=AC+BC,
即AP+BP≧AC+BC
∴沿折线A-C-B的路线行走时路程最短。
1.如图,AB垂直平分线段CD,垂足为点B,点E、F是AB上的点,CD=40,AB=35,则图中阴影部分的面积是 。
当堂检测
350
A
B
A′
2、如图,EFGH是矩形的台球桌面,有两球分别位于A、B两点的位置,试问怎样撞击A球,才能使A球先碰撞台边EF反弹后再击中B球?
E
F
G
H
解:1.作点A关于EF的对称点A′
2.连结A′B交EF于点C则沿AC撞击黑球A,必沿CB反弹击中白球B。
C
3、如图已知直角三角形ABC。
(1)以直角边AC所在的直线为对称轴,作出与直角三角形ABC成轴对称的图形
(2)第(1)题作出的图形和原图形组成一个等腰三角形吗?请说明理由。
课堂小结
一个概念:
轴对称图形
一个性质:
轴对称图形的性质
对称轴垂直平分连结两个对称点之间的线段。
两种技能:
(1)作轴对称图形的对称轴;
(2)作轴对称图形中已知点的对称点.
应用轴对称图形的性质作图:
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
