2021-2022学年浙教版数学八年级上册 2.7探索勾股定理---从勾股定理到图形面积关系的拓展 课件(共23张PPT)
文档属性
| 名称 | 2021-2022学年浙教版数学八年级上册 2.7探索勾股定理---从勾股定理到图形面积关系的拓展 课件(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-06 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
环节一:复习导入,引发思考
1.勾股定理用文字语言来表述,是怎样的?
2.已知:如图,在 Rt△ABC中,∠C=90°,AB=c,AC=b,BC=a,写出a,b,c之间的关系式.
直角三角形两条直角边的平方和等于斜边的平方.
3.如图,分别以a、b、c为一边向外作三个正方形,对应的正方形面积记为S1、S2、S3.思考:S1、S2与S3有怎样的等量关系?请用一个等式表示出来.
4.结合右边的图形,用一句话来概括勾股定理与图形面积的关系.
归纳:分别以直角三角形两条直角边为边长的两个正方形面积之和,等于以斜边为边长的正方形面积.
从勾股定理
到图形面积关系的拓展
2021年10月20日
实验欣赏
研究的极致
环节二:自主合作,学会探究
思考:
1.如果以直角三角形三边为基本要素,分别向外作其它图形,那么这个结论还成立吗?
2.要回答这个问题,请按照下面的步骤先自主探究,然后与你的同伴交流你的发现及探索过程.
步骤:
1.选择你熟悉的几何图形,在备用图上作出要探究的图形.
2.通过观察、测量等操作方法,你发现了什么?请给出你的猜想.
.
操作发现
大胆猜想
小心求证
归纳小结
3.写出你的验证过程.
4.归纳刚刚证得的结论.
“在一个直角三角形中,在斜边上所画的任何图形的面积,等于在两条直角边上所画的与其相似的图形面积之和.”
环节三:图形再探,激活思维
思考:
刚才我们分别以直角三角形的三边向形“外”作图,然后开展探究活动.
数学家总是很喜欢从“反面”来思考问题,所以按照这个想法,你觉得接下来该如何研究?
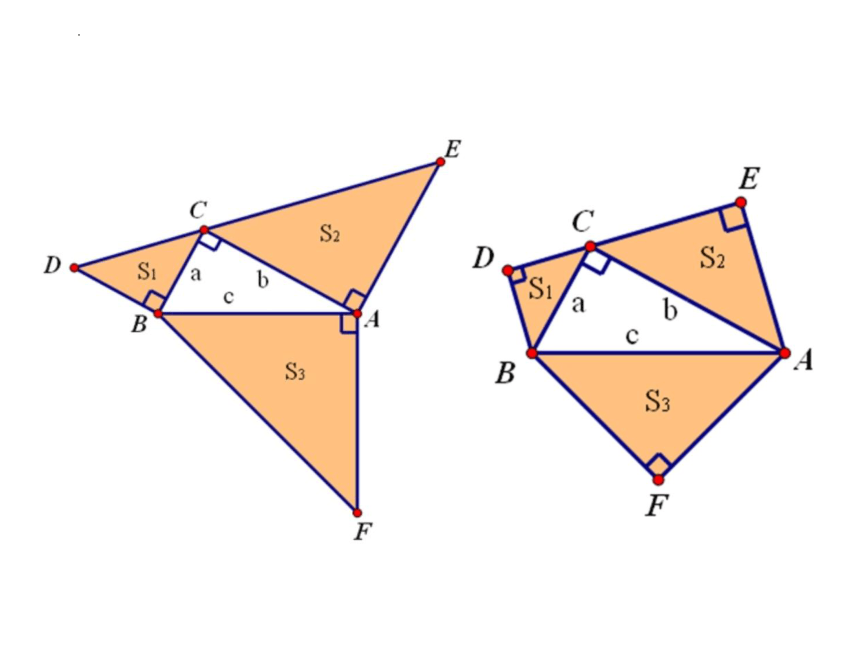
1.如图(1)左图,如果把以斜边为一边的正方形向形“内”作图,而其它两个正方形不变,从而得到(1)右图.
思考:绿色图形的面积之和与紫色图形的面积之和有怎样的数量关系?
2.对(2)中左图按照同样的方法操作,得到了图(2)中的两个月牙.
“两个月牙形的面积之和,等于这个直角三角形的面积,即S1+S2=S5.”你能说明理由吗?
关于这两个月牙形与直角三角形的面积关系,古希腊数学家希波克拉底大约在公元前400年就给出了如下结论:
1.在前面的探究中我们已经知道:
“在一个直角三角形中,在斜边上所画的任何图形的面积,等于在两条直角边上所画的与其相似的图形面积之和.”
请看下面的材料:
环节四:拓展升华,情理交融
那么这个结论是不是一定不成立了呢?
不相似
任意三角形
“设ABC是任意三角形,CADE和CBFG是在两边CA和CB两侧所画的任何两个平行四边形,设DE和FG相交于点H,作AL和BM与HC平行且相等,三个平行四边形面积别记为S1、S2、S3.则S1+S2=S3."(如图)
这个结论的证明留给大家课后去探索.
在古希腊时代,亚历山大里亚的帕普斯(Pappus,大约公元前300年)在他的《数学汇编》(Mathematical Collection)一书的第4卷中给出了一个令人注目的关于勾股定理的推广.
2.我们知道直角三角形是平面图形,对应的勾股定理表达式是a2+b2=c2.
a2+b2=c2
三维
二维
?
a2+b2+c2=d2
如果平面图形拓展到立体图形,比如长方体(如图),那么长方体中是否也存在类似的平方关系呢?
3.勾股定理表达式是a2+b2=c2,从代数角度看,可以提出如下问题:
是否可以找到一组正整数(a,b,c)使得这个等式成立?
像勾股数(3,4,5);(5,12,13)等都是符合要求的正整数解.
思考:
如果从“次数” 上进行推广,我们可以提出怎样的问题?
费马大定理,又被称为“费马猜想”,常见的表述为:
当整数n>2时,关于xn + yn = zn 的方程没有正整数解.
最大成就:
证明了费马大定理.
环节五:导图梳理,建构内化
边角推广
立体推广
数推广
形外
形内
形
数
勾股定理
a2+b2=c2
特例:正方形
Sa+Sb=Sc
月牙定理
一般:相似形
Sa+Sb=Sc
费马大定理
特例:长方体
a2+b2+c2=d2
帕普斯推广
勾股数
【当堂检测】
1. 已知:如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形 ,若正方形 A ,B ,C ,D 的面积分别是9,25,4,9则最大正方形G的面积是 .
图(1)
图(2)
2.勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中曾有记载.以直角三角形的各边为边分别向外作正方形如图1,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.
(A)直角三角形的面积.
(B)最大正方形的面积.
(C)较小两个正方形重叠的面积.
(D)最大正方形与直角三角形的面积之和.
如果知道图中阴影部分的面积.则一定能求出( ).
作业:
搜索并学习勾股定理拓展的数学历史,然后写一篇数学小论文.
环节一:复习导入,引发思考
1.勾股定理用文字语言来表述,是怎样的?
2.已知:如图,在 Rt△ABC中,∠C=90°,AB=c,AC=b,BC=a,写出a,b,c之间的关系式.
直角三角形两条直角边的平方和等于斜边的平方.
3.如图,分别以a、b、c为一边向外作三个正方形,对应的正方形面积记为S1、S2、S3.思考:S1、S2与S3有怎样的等量关系?请用一个等式表示出来.
4.结合右边的图形,用一句话来概括勾股定理与图形面积的关系.
归纳:分别以直角三角形两条直角边为边长的两个正方形面积之和,等于以斜边为边长的正方形面积.
从勾股定理
到图形面积关系的拓展
2021年10月20日
实验欣赏
研究的极致
环节二:自主合作,学会探究
思考:
1.如果以直角三角形三边为基本要素,分别向外作其它图形,那么这个结论还成立吗?
2.要回答这个问题,请按照下面的步骤先自主探究,然后与你的同伴交流你的发现及探索过程.
步骤:
1.选择你熟悉的几何图形,在备用图上作出要探究的图形.
2.通过观察、测量等操作方法,你发现了什么?请给出你的猜想.
.
操作发现
大胆猜想
小心求证
归纳小结
3.写出你的验证过程.
4.归纳刚刚证得的结论.
“在一个直角三角形中,在斜边上所画的任何图形的面积,等于在两条直角边上所画的与其相似的图形面积之和.”
环节三:图形再探,激活思维
思考:
刚才我们分别以直角三角形的三边向形“外”作图,然后开展探究活动.
数学家总是很喜欢从“反面”来思考问题,所以按照这个想法,你觉得接下来该如何研究?
1.如图(1)左图,如果把以斜边为一边的正方形向形“内”作图,而其它两个正方形不变,从而得到(1)右图.
思考:绿色图形的面积之和与紫色图形的面积之和有怎样的数量关系?
2.对(2)中左图按照同样的方法操作,得到了图(2)中的两个月牙.
“两个月牙形的面积之和,等于这个直角三角形的面积,即S1+S2=S5.”你能说明理由吗?
关于这两个月牙形与直角三角形的面积关系,古希腊数学家希波克拉底大约在公元前400年就给出了如下结论:
1.在前面的探究中我们已经知道:
“在一个直角三角形中,在斜边上所画的任何图形的面积,等于在两条直角边上所画的与其相似的图形面积之和.”
请看下面的材料:
环节四:拓展升华,情理交融
那么这个结论是不是一定不成立了呢?
不相似
任意三角形
“设ABC是任意三角形,CADE和CBFG是在两边CA和CB两侧所画的任何两个平行四边形,设DE和FG相交于点H,作AL和BM与HC平行且相等,三个平行四边形面积别记为S1、S2、S3.则S1+S2=S3."(如图)
这个结论的证明留给大家课后去探索.
在古希腊时代,亚历山大里亚的帕普斯(Pappus,大约公元前300年)在他的《数学汇编》(Mathematical Collection)一书的第4卷中给出了一个令人注目的关于勾股定理的推广.
2.我们知道直角三角形是平面图形,对应的勾股定理表达式是a2+b2=c2.
a2+b2=c2
三维
二维
?
a2+b2+c2=d2
如果平面图形拓展到立体图形,比如长方体(如图),那么长方体中是否也存在类似的平方关系呢?
3.勾股定理表达式是a2+b2=c2,从代数角度看,可以提出如下问题:
是否可以找到一组正整数(a,b,c)使得这个等式成立?
像勾股数(3,4,5);(5,12,13)等都是符合要求的正整数解.
思考:
如果从“次数” 上进行推广,我们可以提出怎样的问题?
费马大定理,又被称为“费马猜想”,常见的表述为:
当整数n>2时,关于xn + yn = zn 的方程没有正整数解.
最大成就:
证明了费马大定理.
环节五:导图梳理,建构内化
边角推广
立体推广
数推广
形外
形内
形
数
勾股定理
a2+b2=c2
特例:正方形
Sa+Sb=Sc
月牙定理
一般:相似形
Sa+Sb=Sc
费马大定理
特例:长方体
a2+b2+c2=d2
帕普斯推广
勾股数
【当堂检测】
1. 已知:如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形 ,若正方形 A ,B ,C ,D 的面积分别是9,25,4,9则最大正方形G的面积是 .
图(1)
图(2)
2.勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中曾有记载.以直角三角形的各边为边分别向外作正方形如图1,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.
(A)直角三角形的面积.
(B)最大正方形的面积.
(C)较小两个正方形重叠的面积.
(D)最大正方形与直角三角形的面积之和.
如果知道图中阴影部分的面积.则一定能求出( ).
作业:
搜索并学习勾股定理拓展的数学历史,然后写一篇数学小论文.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
