1.4.1 二次函数的应用(百分率、利润问题)(含解析)
文档属性
| 名称 | 1.4.1 二次函数的应用(百分率、利润问题)(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-22 10:05:38 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
二次函数应用(百分率、利润问题)
一、单选题
1.据省统计局公布的数据,合肥市2021年第一季度GDP总值约为2.4千亿元人民币,若我市第三季度GDP总值为y千亿元人民币,平均每个季度GDP增长的百分率为x,则y关于x的函数表达式是( )
A. B.
C. D.
2.某超市一月份的营业额是100万元,月平均增加的百分率相同,第一季度的总营业额是364万元,若设月平均增长的百分率是 ,那么可列出的方程是( )
A. ; B. ;
C. ; D. .
二、填空题
3.为执行国家药品降价政策,给人民群众带来实惠,某药品经过两次降价,每瓶零售价由100元降为81元,则平均每次降价的百分率是 .
4.某商品原价为180元,连续两次提价后售价为300元,且每次提价的百分率相等,设每次提价的百分率为x,依题意可列方程 .
5.受供求关系影响,去年猪肉价格经过连续两轮涨价,价格从40元/千克涨到90元/千克,若两轮涨价的百分率相同,则这个百分率是 .
三、综合题
6.从上饶到杭州的火车原来的平均速度是180千米/时,经过两次提速后平均速度为217.8千米/时,这两次提速的百分率相同.
(1)求该火车每次提速的百分率;
(2)填空:若上饶到杭州的铁路长396千米,则第一次提速后从上饶到杭州所用的时间比提速前少了 小时.
7.2015年底某市汽车拥有量为100万辆,而截止到2017年底,该市的汽车拥有量已达到144万辆.
(1)求2015年底至2017年底该市汽车拥有量的年平均增长率;
(2)若年增长率保持不变,预计2018年底该市汽车拥有量将达到多少万辆.
8.随着疫情防控形势稳步向好,“复工复产”成为主旋律。某生产无人机公司统计发现,公司今年2月份生产A型无人机2000架,4月份生产A型无人机达到12500架。
(1)求该公司生长A型无人机每月产量的平均增长率;
(2)该公司还生产B型无人机,已知生产1架A型无人机的成本200元,生产1架B型无人机的成本是300元,再要生产A、B两种型号无人机共100架,其中A型无人机数量不超过B型无人机数量的3倍。公司生产A、B两种型号无人机各多少架时才可使生产成本最少?
9.某种商品每件的进价为10元,若每件按20元的价格销售,则每月能卖出360件;若每件按30元的价格销售,则每月能卖出60件.假定每月的销售件数y是销售价格x(单位:元)的一次函数.
(1)求y关于x的一次函数解析式;
(2)当销售价格定为多少元时,每月获得的利润最大?并求此最大利润.
10.大学生自主创业,集资5万元开品牌专卖店,已知该品牌商品成本为每件a元,市场调查发现日销售量y(件)与销售价x(元/件)之间存在一次函数关系如表:
销售价x(元/件) … 110 115 120 125 130 …
销售量y(件) … 50 45 40 35 30 …
若该店某天的销售价定为110元/件,雇有3名员工,则当天正好收支平衡(其中支出=商品成本+员工工资+应支付其它费用):已知员工的工资为每人每天100元,每天还应支付其它费用为200元(不包括集资款).
(1)求日销售量y(件)与销售价x(元/件)之间的函数关系式;
(2)该店现有2名员工,试求每件服装的销售价定为多少元时,该服装店每天的毛利润最大:(毛利润═销售收入一商品成本一员工工资一应支付其他费用)
(3)在(2)的条件下,若每天毛利润全部积累用于一次性还款,而集资款每天应按其万分之二的利率支付利息,则该店最少需要多少天(取整数)才能还清集资款?
11.2022年在中国举办的冬奥会和残奥会令世界瞩目,冬奥会和残奥会的吉祥物冰墩墩和雪容融家喻户晓,成为热销产品,某商家以每套34元的价格购进一批冰墩墩和雪容融套件,若该产品每套的售价是48元时,每天可售出200套;若每套售价提高2元,则每天少卖4套.
(1)设冰墩墩和雪容融套件每套售价定为x元时,求该商品销售量y与x之间的函数关系式;
(2)求每套售价定为多少元时,每天销售套件所获利润W最大,最大利润是多少元?
12.荔枝是夏季的时令水果,储存不太方便.某水果店将进价为18元/千克的荔枝,以28元/千克售出时,每天能售出40千克.市场调研表明:当售价每降低1元/千克时,平均每天能多售出10千克.设降价x元.
(1)降价后平均每天可以销售荔枝 千克.(用含x的代数式表示)
(2)设销售利润为y,请写出y关于x的函数关系式.
(3)该水果店想要使荔枝的销售利润平均每天达到480元,且尽可能地减少库存压力,应将价格定为多少元/千克?
13.某企业投入60万元(只计入第一年成本)生产某种产品,按网上订单生产并销售(生产量等于销售量).经测算,该产品网上每年的销售量y(万件)与售价x(元/件)之间满足函数关系式y=24-x,第一年除60万元外其他成本为8元/件.
(1)求该产品第一年的利润w(万元)与售价x之间的函数关系式;
(2)该产品第一年利润为4万元,第二年将它全部作为技改资金再次投入(只计入第二年成本)后,其他成本下降2元/件.①求该产品第一年的售价;②若第二年售价不高于第一年,销售量不超过13万件,则第二年利润最少是多少万元?
14.某花卉市场店铺老板用5400元按批发价购买了一批花卉.若将批发价降低,则可以多购买该花卉20盆.据市场调查反映,该花卉每盆售价42元时,每天可卖出20盆;若调整价格,每盆花卉每涨价2元,每天要少卖出1盆.
(1)该花卉每盆批发价是多少元?
(2)店铺老板决定在每盆售价42元的基础上,每盆花卉涨价不超过10元,问该花卉一天最大的销售利润是多少元?
(3)该店铺开展快递托运送货到家活动,但每盆花卉店铺还需增加a元的快递成本,若每盆花卉售价不低于62元时,每天的利润将随着售价的增长不断降低,请直接写出快递成本最多是多少元?
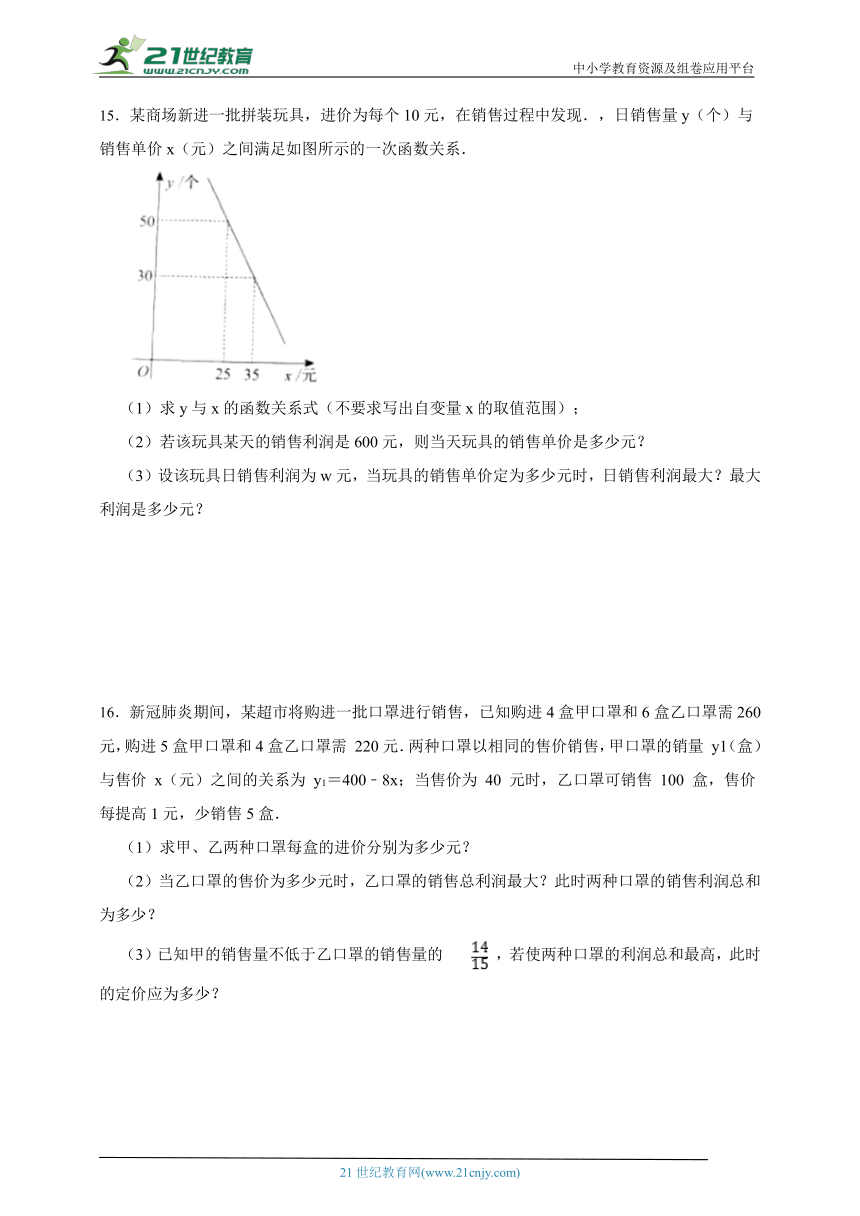
15.某商场新进一批拼装玩具,进价为每个10元,在销售过程中发现.,日销售量y(个)与销售单价x(元)之间满足如图所示的一次函数关系.
(1)求y与x的函数关系式(不要求写出自变量x的取值范围);
(2)若该玩具某天的销售利润是600元,则当天玩具的销售单价是多少元?
(3)设该玩具日销售利润为w元,当玩具的销售单价定为多少元时,日销售利润最大?最大利润是多少元?
16.新冠肺炎期间,某超市将购进一批口罩进行销售,已知购进4盒甲口罩和6盒乙口罩需260元,购进5盒甲口罩和4盒乙口罩需 220元.两种口罩以相同的售价销售,甲口罩的销量 y1(盒)与售价 x(元)之间的关系为
y1=400﹣8x;当售价为 40 元时,乙口罩可销售 100 盒,售价每提高1元,少销售5盒.
(1)求甲、乙两种口罩每盒的进价分别为多少元?
(2)当乙口罩的售价为多少元时,乙口罩的销售总利润最大?此时两种口罩的销售利润总和为多少?
(3)已知甲的销售量不低于乙口罩的销售量的 ,若使两种口罩的利润总和最高,此时的定价应为多少?
答案解析部分
1.【答案】C
【解析】【解答】解:已知平均每个季度 增长的百分率为 ,
则 关于 的函数表达式是: .
故答案为:C.
【分析】根据“当前季度的GDP=前一个季度的GDP×(1+增长率)”可列出函数表达式。
2.【答案】B
【解析】【解答】解:根据题意可得,100+100(1+x)+100(1+x)2=364
故答案为:B.
【分析】根据题意,由一月份的营业额,相同的百分率以及总营业额,列出方程即可。
3.【答案】10%
【解析】【解答】设平均每次降价的百分率是
根据题意,得:
∴
根据题意,得:
∴
∴ ,即
故答案为:10%.
【分析】设平均每次降价的百分率是 ,经过两轮降价后“现价=原价×(1-降价率)2,依此列方程求解即可.
4.【答案】
【解析】【解答】解:根据题意可得,180(1+x%)2=300
【分析】根据题意,由等量关系列出方程即可。
5.【答案】50%
【解析】【解答】设百分率为x 可列出40(1+x)2=90,可解出x=50%
【分析】根据涨价率与价格的关系,可列出方程。
6.【答案】(1)解:设该火车每次提速的百分率为x,
根据题意,得: ,解得: (舍去),
答:该火车每次提速的百分率为10%;
(2)0.2
【解析】【解答】解:(2)第一次提速后的速度为 (千米/时)
∴ (小时),
故答案为:0.2.
【分析】(1)设该火车每次提速的百分率为x,根据“两次提速后平均速度为217.8千米/时”列方程求解即可;(2)利用(1)求出第一次的速度,再求出第一次、第二次的时间,最后作差求解即可。
7.【答案】(1)解:设2015年底至2017年底该市汽车拥有量的年平均增长率为x,
由题意得:100(1+x)2=144,
解得:x1=0.2=20%,x2=﹣2.2(不合题意,舍去),
答:2015年底至2017年底,该市汽车拥有量的年平均增长率为20%
(2)解:144×(1+20%)=172.8(万辆)
答:预计2018年底该市汽车拥有量将达到172.8万辆.
【解析】【分析】(1)可以设年平均增长率为x,根据2015年和2017年汽车的数量即可列出方程,求出x的值即可。
(2)根据(1)中求出的增长率,计算2018年的汽车拥有量即可。
8.【答案】(1)解:设平均增长率为x
∴2000(1+x)2=12500
∴x1= ,x2= (舍)
∴增长率为150%
(2)解:设A型x架,则B型(100-x)架
∴x≤3(100-x)
X≤75
生产成本W=200x+300(100-x)
=-100x+30000
∴当x最大时,W最小
∴x=75时,Wmin=22500元
∴A型75架,B架25架。
【解析】【分析】(1)设公司的平均增长率为x,根据2月份以及4月份的数量,即可得到关于x的方程,求出答案即可。
(2)可以设A型号的数量为x,则B型号的数量为(100-x),那么根据A的数量不超过B的3倍,即可得到不等式,求出答案即可。
9.【答案】(1)解:设,把,和,代入可得
,
解得,
则;
(2)解:每月获得利润
.
∵,
∴当时,P有最大值,最大值为3630.
答:当价格为21元时,才能使每月获得最大利润,最大利润为3630元.
【解析】【分析】(1)设,再利用待定系数法求出函数解析式即可;
(2)根据题意列出函数解析式,再利用二次函数的性质求解即可。
10.【答案】(1)解:由表可知,y是关于x的一次函数,设y=kx+b,
将x=110、y=50,x=115、y=45代入,
得: ,
解得: ,
∴y=-x+160
(2)解:由已知可得:50×110=50a+3×100+200,
解得:a=100,
设每天的毛利润为W,
则W=(x-100)y-2×100-200
=(x-100)(-x+160)-2×100-200
=-x2+260x-16400
=-(x-130)2+500,
∴当x=130时,W取得最大值,最大值为500,
答:每件服装的销售价定为130元时,该服装店每天的毛利润最大,最大利润为500元
(3)解:设需t天能还清借款,
则500t≥50000+0.0002×50000t
解得:t≥102 ,
∵t为整数,
∴t的最小值为103,
答:该店最少需要103天才能还清集资款
【解析】【分析】(1)由表格中的信息用待定系数法可求一次函数的解析式;
(2)根据当天正好收支平衡(其中支出=商品成本+员工工资+应支付其它费用)列出关于成本a的值,再根据毛利润═销售收入一商品成本一员工工资一应支付其他费用列出解析式,并将求得的解析式配成顶点式用二次函数的性质即可求解;
(3)由(2)知,W的最大值为500,设需t天能还清借款,则由题意可得t天所还的款大于或等于本金+利息,列不等式即可求解。
11.【答案】(1)解:根据题意,得
与x之间的函数关系式是
(2)解:根据题意,得
∴抛物线开口向下,W有最大值
当 时,
答:每套售价为91元时,每天销售套件所获利润最大,最大利润是6498元.
【解析】【分析】(1)由题意可得当售价为x元时,每天可多少卖×4(x-48)套,利用200减去少卖的套数可得y与x的关系式;
(2)根据(售价-进价)×销售量可得W关于x的关系式,然后结合二次函数的性质进行解答.
12.【答案】(1)40+10x
(2)解:
整理得
(3)解:即,代入函数得,
解方程,得,
因为要尽可能地清空库存,所以舍去取
此时荔枝定价为(元/千克)
答:应将价格定为24元/千克。
【解析】【分析】(1)根据“当售价每降低1元/千克时,平均每天能多售出10千克”写出表达式即可;
(2)根据“销售利润=销售数量×(售价-进价)”建立y关于x的函数关系式即可;
(3)利用(2)的结果,结合每天的销售利润达到480元,建立关于x的方程求解, 最后确定定价,应考虑尽可能地减少库存压力.
13.【答案】(1)解:由题意得:
(2)解:①由(1)得:当 时,
则 即
解得:
即第一年的售价为每件16元,
② 第二年售价不高于第一年,销售量不超过13万件,
解得:
其他成本下降2元/件,
∴
对称轴为
当 时,利润最高,为77万元,而
当 时, (万元)
当 时, (万元)
所以第二年的最低利润为 万元.
【解析】【分析】(1)根据总利润=每件利润×销售量-投资成本,列出函数关系式即可;
(2) ①由(1)得W求出W=4时x的值即可;②根据“第二年售价不高于第一年,销售量不超过13万件”列出不等式组,可求出x的范围,根据总利润=每件利润×销售量-投资成本,列出函数关系式,再利用二次函数的性质求解即可.
14.【答案】(1)解:设批发价是x元,由题意可得:
,
解得x=30,
经检验,x=30是原方程解,
答:花卉每盆批发价30元;
(2)解:设涨价m元(0<m≤10),利润W元,
W=(42+m-30)(20﹣)=-m2+14m+240,
对称轴是m=14,且-<0开口向下,
∵0<m≤10
∴当m=10时,W有最大值,是330元;
(3)解:快递成本最多是12元.
【解析】【解答】解:(3)W=(42+m-30-a)(20-m)=-m2+(14+)m+240-20a,
∵42+m≥62,
∴m≥20,
∵利润随售价增长而降低,
∴对称轴m=14+≤20,
∴a≤12,
∴快递成本最多是12元.
【分析】(1) 设批发价是x元,根据题意列出分式方程解之即可;
(2)设涨价m元(0<m≤10),利润W元, 求出函数解析式,根据二次函数的性质即可求出最大利润;
(3)根据二次函数的性质即可求出答案。
15.【答案】(1)解:由图可知,设一次函数的解析式为,
把点(25,50)和点(35,30)代入,得
,解得,
∴一次函数的解析式为;
(2)解:根据题意,设当天玩具的销售单价是元,则
,
解得:,,
∴当天玩具的销售单价是40元或20元;
(3)解:根据题意,则
,
整理得:;
∵,
∴当时,有最大值,最大值为800;
∴当玩具的销售单价定为30元时,日销售利润最大;最大利润是800元.
【解析】【分析】(1)利用待定系数法求函数解析式即可;
(2)根据该玩具某天的销售利润是600元, 列方程求解即可;
(3)先求出 , 再求解即可。
16.【答案】(1)解:设甲、乙两种口罩每盒的进价分别为 x 元、y 元,由题意得:
解得: .
∴甲、乙两种口罩每盒的进价分别为 20元、30元.
(2)解:设乙口罩的销售利润为 w 元,由题意得:
w=(x﹣30)[100﹣5(x﹣40)]
=﹣5x2+450x﹣9000
=﹣5(x﹣45)2+1125,
∴当乙口罩的售价为 45 元时,乙口罩的销售总利润最大,为1125元.
当售价为 45 元时,y1=400﹣8x=400﹣8×45=40(盒);
∴甲口罩的销售利润为:(45﹣20)×40=1000(元),
∴此时两种口罩的销售利润总和为:1125+1000=2125(元).
∴当乙口罩的售价为 45 元时,乙口罩的销售总利润最大,此时两种口罩的销售利润总和为 2125 元.
(3)解:由题意得:
解得:x≤36,
∵两种口罩的利润总和 w 总=(400﹣8x)(x﹣20)+(﹣5x2+450x﹣9000)
=﹣13x2+1010x﹣17000,
∴对称轴为: ,
∴当 x=36 时,两种口罩的利润总和最高.
∴若使两种口罩的利润总和最高,此时的定价应为 36 元.
【解析】【分析】(1)设甲、乙两种口罩每盒的进价分别为 x 元、y 元,根据“ 购进4盒甲口罩和6盒乙口罩需260元,购进5盒甲口罩和4盒乙口罩需 220元 ”,列出二元一次方程组求解,即可解答;
(2)设乙口罩的销售利润为 w 元,根据“利润=单件利润×数量”列出函数关系式,然后根据二次函数的性质求最大值,依此价格计算出甲口罩的销售利润,再求和,即可解答;
(3)根据“ 甲的销售量不低于乙口罩的销售量的 ”,列出不等式求出x的范围,再把两种口罩的利润总和 w 总表示出来,根据二次函数的性质求最大值即可.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
二次函数应用(百分率、利润问题)
一、单选题
1.据省统计局公布的数据,合肥市2021年第一季度GDP总值约为2.4千亿元人民币,若我市第三季度GDP总值为y千亿元人民币,平均每个季度GDP增长的百分率为x,则y关于x的函数表达式是( )
A. B.
C. D.
2.某超市一月份的营业额是100万元,月平均增加的百分率相同,第一季度的总营业额是364万元,若设月平均增长的百分率是 ,那么可列出的方程是( )
A. ; B. ;
C. ; D. .
二、填空题
3.为执行国家药品降价政策,给人民群众带来实惠,某药品经过两次降价,每瓶零售价由100元降为81元,则平均每次降价的百分率是 .
4.某商品原价为180元,连续两次提价后售价为300元,且每次提价的百分率相等,设每次提价的百分率为x,依题意可列方程 .
5.受供求关系影响,去年猪肉价格经过连续两轮涨价,价格从40元/千克涨到90元/千克,若两轮涨价的百分率相同,则这个百分率是 .
三、综合题
6.从上饶到杭州的火车原来的平均速度是180千米/时,经过两次提速后平均速度为217.8千米/时,这两次提速的百分率相同.
(1)求该火车每次提速的百分率;
(2)填空:若上饶到杭州的铁路长396千米,则第一次提速后从上饶到杭州所用的时间比提速前少了 小时.
7.2015年底某市汽车拥有量为100万辆,而截止到2017年底,该市的汽车拥有量已达到144万辆.
(1)求2015年底至2017年底该市汽车拥有量的年平均增长率;
(2)若年增长率保持不变,预计2018年底该市汽车拥有量将达到多少万辆.
8.随着疫情防控形势稳步向好,“复工复产”成为主旋律。某生产无人机公司统计发现,公司今年2月份生产A型无人机2000架,4月份生产A型无人机达到12500架。
(1)求该公司生长A型无人机每月产量的平均增长率;
(2)该公司还生产B型无人机,已知生产1架A型无人机的成本200元,生产1架B型无人机的成本是300元,再要生产A、B两种型号无人机共100架,其中A型无人机数量不超过B型无人机数量的3倍。公司生产A、B两种型号无人机各多少架时才可使生产成本最少?
9.某种商品每件的进价为10元,若每件按20元的价格销售,则每月能卖出360件;若每件按30元的价格销售,则每月能卖出60件.假定每月的销售件数y是销售价格x(单位:元)的一次函数.
(1)求y关于x的一次函数解析式;
(2)当销售价格定为多少元时,每月获得的利润最大?并求此最大利润.
10.大学生自主创业,集资5万元开品牌专卖店,已知该品牌商品成本为每件a元,市场调查发现日销售量y(件)与销售价x(元/件)之间存在一次函数关系如表:
销售价x(元/件) … 110 115 120 125 130 …
销售量y(件) … 50 45 40 35 30 …
若该店某天的销售价定为110元/件,雇有3名员工,则当天正好收支平衡(其中支出=商品成本+员工工资+应支付其它费用):已知员工的工资为每人每天100元,每天还应支付其它费用为200元(不包括集资款).
(1)求日销售量y(件)与销售价x(元/件)之间的函数关系式;
(2)该店现有2名员工,试求每件服装的销售价定为多少元时,该服装店每天的毛利润最大:(毛利润═销售收入一商品成本一员工工资一应支付其他费用)
(3)在(2)的条件下,若每天毛利润全部积累用于一次性还款,而集资款每天应按其万分之二的利率支付利息,则该店最少需要多少天(取整数)才能还清集资款?
11.2022年在中国举办的冬奥会和残奥会令世界瞩目,冬奥会和残奥会的吉祥物冰墩墩和雪容融家喻户晓,成为热销产品,某商家以每套34元的价格购进一批冰墩墩和雪容融套件,若该产品每套的售价是48元时,每天可售出200套;若每套售价提高2元,则每天少卖4套.
(1)设冰墩墩和雪容融套件每套售价定为x元时,求该商品销售量y与x之间的函数关系式;
(2)求每套售价定为多少元时,每天销售套件所获利润W最大,最大利润是多少元?
12.荔枝是夏季的时令水果,储存不太方便.某水果店将进价为18元/千克的荔枝,以28元/千克售出时,每天能售出40千克.市场调研表明:当售价每降低1元/千克时,平均每天能多售出10千克.设降价x元.
(1)降价后平均每天可以销售荔枝 千克.(用含x的代数式表示)
(2)设销售利润为y,请写出y关于x的函数关系式.
(3)该水果店想要使荔枝的销售利润平均每天达到480元,且尽可能地减少库存压力,应将价格定为多少元/千克?
13.某企业投入60万元(只计入第一年成本)生产某种产品,按网上订单生产并销售(生产量等于销售量).经测算,该产品网上每年的销售量y(万件)与售价x(元/件)之间满足函数关系式y=24-x,第一年除60万元外其他成本为8元/件.
(1)求该产品第一年的利润w(万元)与售价x之间的函数关系式;
(2)该产品第一年利润为4万元,第二年将它全部作为技改资金再次投入(只计入第二年成本)后,其他成本下降2元/件.①求该产品第一年的售价;②若第二年售价不高于第一年,销售量不超过13万件,则第二年利润最少是多少万元?
14.某花卉市场店铺老板用5400元按批发价购买了一批花卉.若将批发价降低,则可以多购买该花卉20盆.据市场调查反映,该花卉每盆售价42元时,每天可卖出20盆;若调整价格,每盆花卉每涨价2元,每天要少卖出1盆.
(1)该花卉每盆批发价是多少元?
(2)店铺老板决定在每盆售价42元的基础上,每盆花卉涨价不超过10元,问该花卉一天最大的销售利润是多少元?
(3)该店铺开展快递托运送货到家活动,但每盆花卉店铺还需增加a元的快递成本,若每盆花卉售价不低于62元时,每天的利润将随着售价的增长不断降低,请直接写出快递成本最多是多少元?
15.某商场新进一批拼装玩具,进价为每个10元,在销售过程中发现.,日销售量y(个)与销售单价x(元)之间满足如图所示的一次函数关系.
(1)求y与x的函数关系式(不要求写出自变量x的取值范围);
(2)若该玩具某天的销售利润是600元,则当天玩具的销售单价是多少元?
(3)设该玩具日销售利润为w元,当玩具的销售单价定为多少元时,日销售利润最大?最大利润是多少元?
16.新冠肺炎期间,某超市将购进一批口罩进行销售,已知购进4盒甲口罩和6盒乙口罩需260元,购进5盒甲口罩和4盒乙口罩需 220元.两种口罩以相同的售价销售,甲口罩的销量 y1(盒)与售价 x(元)之间的关系为
y1=400﹣8x;当售价为 40 元时,乙口罩可销售 100 盒,售价每提高1元,少销售5盒.
(1)求甲、乙两种口罩每盒的进价分别为多少元?
(2)当乙口罩的售价为多少元时,乙口罩的销售总利润最大?此时两种口罩的销售利润总和为多少?
(3)已知甲的销售量不低于乙口罩的销售量的 ,若使两种口罩的利润总和最高,此时的定价应为多少?
答案解析部分
1.【答案】C
【解析】【解答】解:已知平均每个季度 增长的百分率为 ,
则 关于 的函数表达式是: .
故答案为:C.
【分析】根据“当前季度的GDP=前一个季度的GDP×(1+增长率)”可列出函数表达式。
2.【答案】B
【解析】【解答】解:根据题意可得,100+100(1+x)+100(1+x)2=364
故答案为:B.
【分析】根据题意,由一月份的营业额,相同的百分率以及总营业额,列出方程即可。
3.【答案】10%
【解析】【解答】设平均每次降价的百分率是
根据题意,得:
∴
根据题意,得:
∴
∴ ,即
故答案为:10%.
【分析】设平均每次降价的百分率是 ,经过两轮降价后“现价=原价×(1-降价率)2,依此列方程求解即可.
4.【答案】
【解析】【解答】解:根据题意可得,180(1+x%)2=300
【分析】根据题意,由等量关系列出方程即可。
5.【答案】50%
【解析】【解答】设百分率为x 可列出40(1+x)2=90,可解出x=50%
【分析】根据涨价率与价格的关系,可列出方程。
6.【答案】(1)解:设该火车每次提速的百分率为x,
根据题意,得: ,解得: (舍去),
答:该火车每次提速的百分率为10%;
(2)0.2
【解析】【解答】解:(2)第一次提速后的速度为 (千米/时)
∴ (小时),
故答案为:0.2.
【分析】(1)设该火车每次提速的百分率为x,根据“两次提速后平均速度为217.8千米/时”列方程求解即可;(2)利用(1)求出第一次的速度,再求出第一次、第二次的时间,最后作差求解即可。
7.【答案】(1)解:设2015年底至2017年底该市汽车拥有量的年平均增长率为x,
由题意得:100(1+x)2=144,
解得:x1=0.2=20%,x2=﹣2.2(不合题意,舍去),
答:2015年底至2017年底,该市汽车拥有量的年平均增长率为20%
(2)解:144×(1+20%)=172.8(万辆)
答:预计2018年底该市汽车拥有量将达到172.8万辆.
【解析】【分析】(1)可以设年平均增长率为x,根据2015年和2017年汽车的数量即可列出方程,求出x的值即可。
(2)根据(1)中求出的增长率,计算2018年的汽车拥有量即可。
8.【答案】(1)解:设平均增长率为x
∴2000(1+x)2=12500
∴x1= ,x2= (舍)
∴增长率为150%
(2)解:设A型x架,则B型(100-x)架
∴x≤3(100-x)
X≤75
生产成本W=200x+300(100-x)
=-100x+30000
∴当x最大时,W最小
∴x=75时,Wmin=22500元
∴A型75架,B架25架。
【解析】【分析】(1)设公司的平均增长率为x,根据2月份以及4月份的数量,即可得到关于x的方程,求出答案即可。
(2)可以设A型号的数量为x,则B型号的数量为(100-x),那么根据A的数量不超过B的3倍,即可得到不等式,求出答案即可。
9.【答案】(1)解:设,把,和,代入可得
,
解得,
则;
(2)解:每月获得利润
.
∵,
∴当时,P有最大值,最大值为3630.
答:当价格为21元时,才能使每月获得最大利润,最大利润为3630元.
【解析】【分析】(1)设,再利用待定系数法求出函数解析式即可;
(2)根据题意列出函数解析式,再利用二次函数的性质求解即可。
10.【答案】(1)解:由表可知,y是关于x的一次函数,设y=kx+b,
将x=110、y=50,x=115、y=45代入,
得: ,
解得: ,
∴y=-x+160
(2)解:由已知可得:50×110=50a+3×100+200,
解得:a=100,
设每天的毛利润为W,
则W=(x-100)y-2×100-200
=(x-100)(-x+160)-2×100-200
=-x2+260x-16400
=-(x-130)2+500,
∴当x=130时,W取得最大值,最大值为500,
答:每件服装的销售价定为130元时,该服装店每天的毛利润最大,最大利润为500元
(3)解:设需t天能还清借款,
则500t≥50000+0.0002×50000t
解得:t≥102 ,
∵t为整数,
∴t的最小值为103,
答:该店最少需要103天才能还清集资款
【解析】【分析】(1)由表格中的信息用待定系数法可求一次函数的解析式;
(2)根据当天正好收支平衡(其中支出=商品成本+员工工资+应支付其它费用)列出关于成本a的值,再根据毛利润═销售收入一商品成本一员工工资一应支付其他费用列出解析式,并将求得的解析式配成顶点式用二次函数的性质即可求解;
(3)由(2)知,W的最大值为500,设需t天能还清借款,则由题意可得t天所还的款大于或等于本金+利息,列不等式即可求解。
11.【答案】(1)解:根据题意,得
与x之间的函数关系式是
(2)解:根据题意,得
∴抛物线开口向下,W有最大值
当 时,
答:每套售价为91元时,每天销售套件所获利润最大,最大利润是6498元.
【解析】【分析】(1)由题意可得当售价为x元时,每天可多少卖×4(x-48)套,利用200减去少卖的套数可得y与x的关系式;
(2)根据(售价-进价)×销售量可得W关于x的关系式,然后结合二次函数的性质进行解答.
12.【答案】(1)40+10x
(2)解:
整理得
(3)解:即,代入函数得,
解方程,得,
因为要尽可能地清空库存,所以舍去取
此时荔枝定价为(元/千克)
答:应将价格定为24元/千克。
【解析】【分析】(1)根据“当售价每降低1元/千克时,平均每天能多售出10千克”写出表达式即可;
(2)根据“销售利润=销售数量×(售价-进价)”建立y关于x的函数关系式即可;
(3)利用(2)的结果,结合每天的销售利润达到480元,建立关于x的方程求解, 最后确定定价,应考虑尽可能地减少库存压力.
13.【答案】(1)解:由题意得:
(2)解:①由(1)得:当 时,
则 即
解得:
即第一年的售价为每件16元,
② 第二年售价不高于第一年,销售量不超过13万件,
解得:
其他成本下降2元/件,
∴
对称轴为
当 时,利润最高,为77万元,而
当 时, (万元)
当 时, (万元)
所以第二年的最低利润为 万元.
【解析】【分析】(1)根据总利润=每件利润×销售量-投资成本,列出函数关系式即可;
(2) ①由(1)得W求出W=4时x的值即可;②根据“第二年售价不高于第一年,销售量不超过13万件”列出不等式组,可求出x的范围,根据总利润=每件利润×销售量-投资成本,列出函数关系式,再利用二次函数的性质求解即可.
14.【答案】(1)解:设批发价是x元,由题意可得:
,
解得x=30,
经检验,x=30是原方程解,
答:花卉每盆批发价30元;
(2)解:设涨价m元(0<m≤10),利润W元,
W=(42+m-30)(20﹣)=-m2+14m+240,
对称轴是m=14,且-<0开口向下,
∵0<m≤10
∴当m=10时,W有最大值,是330元;
(3)解:快递成本最多是12元.
【解析】【解答】解:(3)W=(42+m-30-a)(20-m)=-m2+(14+)m+240-20a,
∵42+m≥62,
∴m≥20,
∵利润随售价增长而降低,
∴对称轴m=14+≤20,
∴a≤12,
∴快递成本最多是12元.
【分析】(1) 设批发价是x元,根据题意列出分式方程解之即可;
(2)设涨价m元(0<m≤10),利润W元, 求出函数解析式,根据二次函数的性质即可求出最大利润;
(3)根据二次函数的性质即可求出答案。
15.【答案】(1)解:由图可知,设一次函数的解析式为,
把点(25,50)和点(35,30)代入,得
,解得,
∴一次函数的解析式为;
(2)解:根据题意,设当天玩具的销售单价是元,则
,
解得:,,
∴当天玩具的销售单价是40元或20元;
(3)解:根据题意,则
,
整理得:;
∵,
∴当时,有最大值,最大值为800;
∴当玩具的销售单价定为30元时,日销售利润最大;最大利润是800元.
【解析】【分析】(1)利用待定系数法求函数解析式即可;
(2)根据该玩具某天的销售利润是600元, 列方程求解即可;
(3)先求出 , 再求解即可。
16.【答案】(1)解:设甲、乙两种口罩每盒的进价分别为 x 元、y 元,由题意得:
解得: .
∴甲、乙两种口罩每盒的进价分别为 20元、30元.
(2)解:设乙口罩的销售利润为 w 元,由题意得:
w=(x﹣30)[100﹣5(x﹣40)]
=﹣5x2+450x﹣9000
=﹣5(x﹣45)2+1125,
∴当乙口罩的售价为 45 元时,乙口罩的销售总利润最大,为1125元.
当售价为 45 元时,y1=400﹣8x=400﹣8×45=40(盒);
∴甲口罩的销售利润为:(45﹣20)×40=1000(元),
∴此时两种口罩的销售利润总和为:1125+1000=2125(元).
∴当乙口罩的售价为 45 元时,乙口罩的销售总利润最大,此时两种口罩的销售利润总和为 2125 元.
(3)解:由题意得:
解得:x≤36,
∵两种口罩的利润总和 w 总=(400﹣8x)(x﹣20)+(﹣5x2+450x﹣9000)
=﹣13x2+1010x﹣17000,
∴对称轴为: ,
∴当 x=36 时,两种口罩的利润总和最高.
∴若使两种口罩的利润总和最高,此时的定价应为 36 元.
【解析】【分析】(1)设甲、乙两种口罩每盒的进价分别为 x 元、y 元,根据“ 购进4盒甲口罩和6盒乙口罩需260元,购进5盒甲口罩和4盒乙口罩需 220元 ”,列出二元一次方程组求解,即可解答;
(2)设乙口罩的销售利润为 w 元,根据“利润=单件利润×数量”列出函数关系式,然后根据二次函数的性质求最大值,依此价格计算出甲口罩的销售利润,再求和,即可解答;
(3)根据“ 甲的销售量不低于乙口罩的销售量的 ”,列出不等式求出x的范围,再把两种口罩的利润总和 w 总表示出来,根据二次函数的性质求最大值即可.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
