1.4.3 二次函数的应用(喷水、拱桥、投球问题)(含解析)
文档属性
| 名称 | 1.4.3 二次函数的应用(喷水、拱桥、投球问题)(含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-22 10:05:38 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
二次函数应用(喷水、拱桥、投球问题)
一、填空题
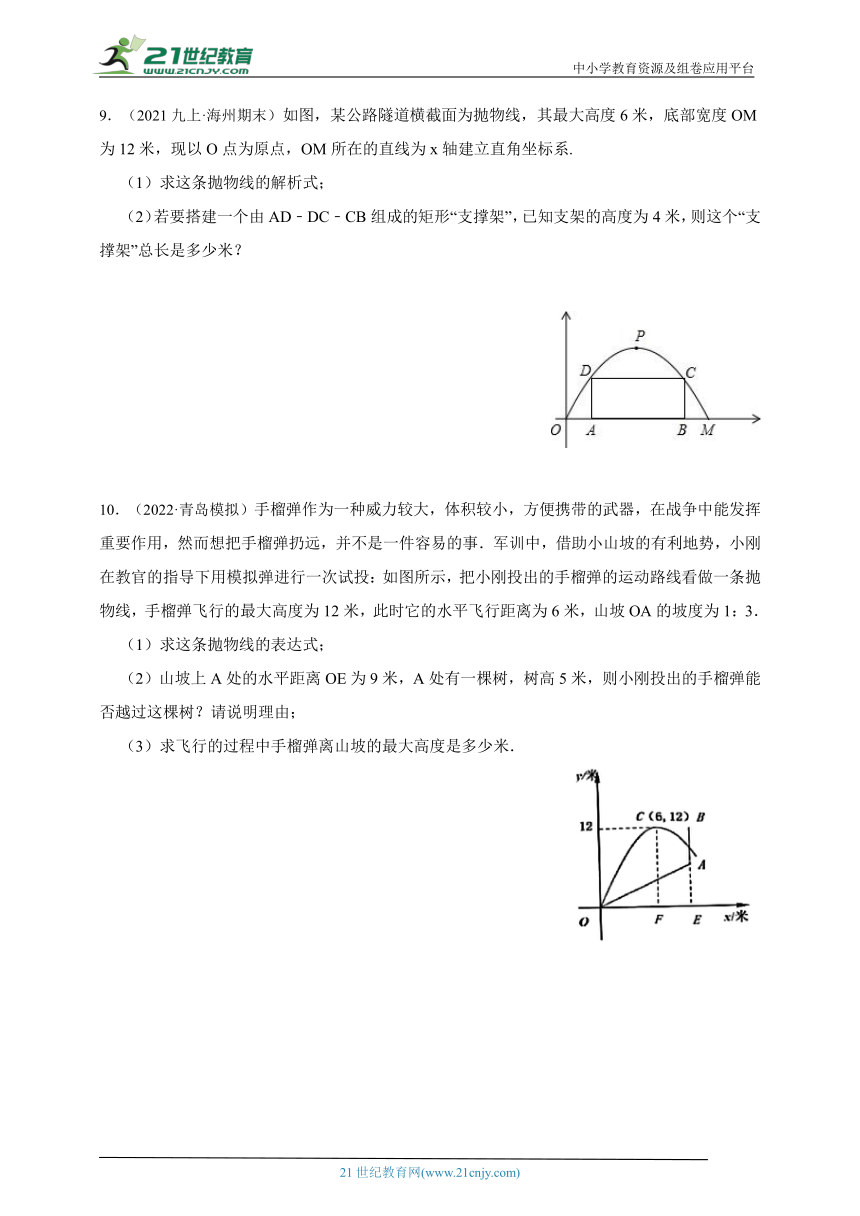
1.(2022·广安)如图是抛物线形拱桥,当拱顶离水面2米时,水面宽6米,水面下降 米,水面宽8米.
2.(2022·武威)如图,以一定的速度将小球沿与地面成一定角度的方向击出时,小球的飞行路线是一条抛物线.若不考虑空气阻力,小球的飞行高度 (单位:m)与飞行时间 (单位:s)之间具有函数关系: ,则当小球飞行高度达到最高时,飞行时间 s.
3.(2022九下·长兴月考)如图是王明正在设计的一动画示意图,×轴上依次有A,B,C三个点,且AB=2,在BC上方有五个台阶(各拐角均为90°),每个台阶的高、宽分别是1和1.5,第一个台阶到x轴距离BD=10.从点A处向右,上方沿抛物线y=-x2+4x+12发出一个带光的点P.当点P落在台阶上时,落点的坐标是 .
4.(2022·衢州模拟)为了在体育中考中取得更好的成绩,小豪积极训练,体育老师对小豪投掷实心球的录像进行技术分析,如图,发现实心球在行进过程中高度y(m)与水平距离x(m)之间的关系为,由此可知小豪此次投掷的成绩是 m.
5.(2022·玉环模拟)斜抛小球,小球触地后呈抛物线反弹,每次反弹后保持相同的抛物线形状(开口方向与开口大小前后一致),第一次反弹后的最大高度为 ,第二次反弹后的最大高度为 ,第二次反弹后,小球越过最高点落在垂直于地面的挡板C处,且离地高度 ,若 ,则 为 .
二、综合题
6.(2022八下·杭州月考)一高尔夫球手某次击出一个高尔夫球的高度h(m)和经过的水平距离d(m)可用公式h=-0.01d2 +d来估计.
(1)当球的水平距离达到50m时.球上升的高度是多少?
(2)当球的高度第一次达到16m时.球的水平距离是多少?
7.(2022·陕西)现要修建一条隧道,其截面为抛物线型,如图所示,线段表示水平的路面,以O为坐标原点,以所在直线为x轴,以过点O垂直于x轴的直线为y轴,建立平面直角坐标系.根据设计要求:,该抛物线的顶点P到的距离为.
(1)求满足设计要求的抛物线的函数表达式;
(2)现需在这一隧道内壁上安装照明灯,如图所示,即在该抛物线上的点A、B处分别安装照明灯.已知点A、B到的距离均为,求点A、B的坐标.
8.(2021九上·全椒期末)某游乐场的圆形喷水池中心O有一雕塑OA,从A点向四周喷水,喷出的水柱为抛物线,且形状相同。如图,以水平方向为x轴,点O为原点建立直角坐标系,点A在y轴上,x轴上的点C、D为水柱的落水点,水柱所在抛物线(第一象限部分)的函数表达式为.
(1)求落水点C、D之间的距离;
(2)若需在OD上离O点10米的E处竖立雕塑EF,,且雕塑的顶部刚好碰到水柱,求雕塑EF的高.
9.(2021九上·海州期末)如图,某公路隧道横截面为抛物线,其最大高度6米,底部宽度OM为12米,现以O点为原点,OM所在的直线为x轴建立直角坐标系.
(1)求这条抛物线的解析式;
(2)若要搭建一个由AD﹣DC﹣CB组成的矩形“支撑架”,已知支架的高度为4米,则这个“支撑架”总长是多少米?
10.(2022·青岛模拟)手榴弹作为一种威力较大,体积较小,方便携带的武器,在战争中能发挥重要作用,然而想把手榴弹扔远,并不是一件容易的事.军训中,借助小山坡的有利地势,小刚在教官的指导下用模拟弹进行一次试投:如图所示,把小刚投出的手榴弹的运动路线看做一条抛物线,手榴弹飞行的最大高度为12米,此时它的水平飞行距离为6米,山坡OA的坡度为1:3.
(1)求这条抛物线的表达式;
(2)山坡上A处的水平距离OE为9米,A处有一棵树,树高5米,则小刚投出的手榴弹能否越过这棵树?请说明理由;
(3)求飞行的过程中手榴弹离山坡的最大高度是多少米.
11.(2022·新昌模拟)一个球从地面竖直向上弹起时的速度为10m/s,经过t(s)时球的高度为h(m).已知物体竖直上抛运动中,(表示物体运动上弹开始的速度,g表示重力系数,取).
(1)写出h(m)关于t(s)的二次函数表达式.
(2)求球从弹起到最高点需要多少时间,最高点的高度是多少?
(3)若球在下落至处时,遇一夹板(这部分运动的函数图象如图所示),球以遇到夹板时的速度再次向上竖直弹起,然后落回地面.求球从最初10m/s弹起到落回地面的时间.
12.(2022九下·定海开学考)某游乐场的圆形喷水池中心O有一雕塑OA,从A点向四周喷水,喷出的水柱为抛物线,且形状相同.如图,以水平方向为x轴,点O为原点建立直角坐标系,点A在y轴上,x轴上的点C,D为水柱的落水点,水柱所在抛物线(第一象限部分)的函数表达式为
(1)求雕塑高OA.
(2)求落水点C,D之间的距离.
(3)若需要在OD上的点E处竖立雕塑EF,OE=10m,EF=1.8m,EF⊥OD.问:顶部F是否会碰到水柱?请通过计算说明.
13.(2022·上虞模拟)如图,以一定的速度将小球沿与地面成一定角度的方向击出时,小球的“飞行路线将是一条抛物线.如果不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有二次函数关系.小明在一次击球过程中测得一些数据,如下表所示.
根据相关信息解答下列问题.
飞行时间t/s 0 1 2
飞行高度h/m 0 15 20
(1)求小球的飞行高度h(单位:m)关于飞行时间t(单位:s)的二次函数关系式.
(2)小球从飞出到落地要用多少时间?
(3)小球的飞行高度能否达到20.5m?如果能,请求出相应的飞行时间;如果不能,请说明理由.
14.(2022九下·义乌月考)用各种盛水容器可以制作精致的家用流水景观(如图1).
科学原理:如图2,始终盛满水的圆柱体水桶水面离地面的高度为H(单位:cm),如果在离水面竖直距离为h(单位:cm)的地方开大小合适的小孔,那么从小孔射出水的射程(水流落地点离小孔的水平距离)s(单位:cm)与h的关系式为s2=4h(H﹣h).
应用思考:现用高度为30cm的圆柱体塑料水瓶做相关研究,水瓶直立地面,通过连续注水保证它始终盛满水,在离水面竖直距离hcm处开一个小孔.
(1)写出s2与h的关系式;并求出当h为何值时,射程s有最大值,最大射程是多少?
(2)在侧面开两个小孔,这两个小孔离水面的竖直距离分别为a,b,要使两孔射出水的射程相同,求a,b之间的关系式;
(3)如果想通过垫高塑料水瓶,使射出水的最大射程增加18cm,求垫高的高度及小孔离水面的竖直距离.
15.(2022·河北模拟)如图所示.三孔桥横截面的三个孔是都呈抛物线形,两小孔形状、大小都相同.正常水位时,大孔水面宽度AB为10m,顶点M距水面6m(即),小孔顶点N距水面4m(即),建立如图所示的平面直角坐标系.
(1)求出大孔抛物线的解析式;
(2)现有一艘船高度是4.5m,宽度是4m,为了保证安全,船顶距离桥拱顶部至少0.5m,则这艘船在正常水位时能否安全通过拱桥大孔?
(3)当水位上涨到刚好淹没小孔时,求出此时大孔的水面宽度EF.
16.(2022·石家庄模拟)如图1的小山丘是科研部门的小球弹射实验场地,在小山丘一侧的山坡上建有小球弹射发射装置,另一侧建有圆柱形小球接收装置,如图2为实验场地的纵截面示意图,小山丘纵截面的外部轮廓线近似为抛物线的一部分,以小山丘纵截面与地面的交线为x轴,以过发射装置所在的直线AB为y轴,建立平面直角坐标系,发射装置底部在轮廓线的点A处,距离地面为1米,在发射装置3米的点B处是发射点,已知小山丘纵截面的外部轮廓线为,从发射装置的发射点弹射一个小球(忽略空气阻力)时,小球的飞行路线为一段抛物线.
(1)直接写出c的值,当小球离B处的水平距离和竖直距离都为4米时,求b的值,并求小球到小山丘的竖直距离为1米时,小球离B处的水平距离;
(2)若小球最远着陆点到y轴的距离为15米,当小球飞行到小山丘顶的正上方,且与顶部距离不小于米时,求b的取值范围,并求小球飞行路线的顶点到x轴距离的最小值;
(3)圆柱形小球接收装置的最大截面为矩形CDEF,已知点E在上,其横坐标为14,轴,,.若小球恰好落入该装置内(不触碰装置侧壁),请直接写出b的取值范围.
17.(2022·胶州模拟)如图1是一座抛物线型拱桥,图2是其在直角坐标系中的侧面示意图.在正常水位时水面宽,此时水面离桥拱顶部的距离为.
(1)按如图2所示的直角坐标系,求此抛物线的函数表达式;
(2)如图3,因某种需要,在桥拱顶部及桥的两端树立了三根支柱,,架设钢缆,在钢缆和桥面之间竖直悬挂若干安全绳,过相邻支柱顶端的钢缆具有相同的抛物线形状,且左、右两条抛物线关于轴对称,左面钢缆抛物线可以用表示.
①求左、右面两条钢缆的最低点之间的距离是多少?
②求安全绳长度(钢缆和桥面之间距离)的最小值是多少?
18.(2022·顺义模拟)某公园内的人工湖里有一组小型喷泉,水柱从位于湖面上方的水枪喷出,水柱落于湖面的路径形状是抛物线.现测量出如下数据,在距离水枪水平距离为d米的地点,水柱距离湖面高度为h米.
d(米) 0 0.5 2.0 3.5 5
h(米) 1.67 2. 25 3.00 2. 25 0
请解决以下问题:
(1)在下面网格中建立适当的平面直角坐标系,根据已知数据描点,并用平滑的曲线连接;
(2)请结合所画图象,水柱最高点距离湖面的高度是 米;
(3)求抛物线的表达式,并写出自变量的取值范围;
(4)现有一游船宽度为2米,顶棚到湖面的高度为2.5米.要求游船从喷泉水柱中间通过时,顶棚不碰到水柱.请问游船是否能符合上述要求通过?并说明理由.
答案解析部分
1.【答案】
【解析】【解答】解:建立平面直角坐标系,设横轴x通过AB,纵轴y通过AB中点O且通过C点,则通过画图可得知O为原点,由题意可得:AO=OB=3米,C坐标为(0,2),
通过以上条件可设顶点式y=ax2+2,把点A点坐标(3,0)代入得,
∴,
∴,
∴抛物线解析式为:;
当水面下降,水面宽为8米时,有
把代入解析式,得;
∴水面下降米;
故答案为:.
【分析】建立平面直角坐标系,设横轴x通过AB,纵轴y通过AB中点O且通过C点,则通过画图可得知O为原点,由题意可得:AO=OB=3米,C(0,2),设y=ax2+2,把A点坐标代入求出a的值,据此可得抛物线的解析式,令x=4,求出y的值,据此解答.
2.【答案】2
【解析】【解答】解:∵h=-5t2+20t=-5(t-2)2+20,且-5<0,
∴当t=2时,h取最大值20.
故答案为:2.
【分析】将h与t的函数关系式化为顶点式,据此可得h的最大值.
3.【答案】(5,7)
【解析】【解答】解:如图所示,以BD的延长线为y轴,AB所在直线为x轴建立平面直角坐标系,
∵每个台阶的高、宽分别是1和1.5,第一个台阶到x轴距离BD=10,
∴对于①~⑤个台阶有:
台阶①:0≤x≤1.5,y=10;
台阶②:1.5<x≤3,y=9;
台阶③:3<x≤4.5,y=8;
台阶④:4.5<x≤6,y=7;
台阶⑤:6<x≤7.5,y=6,
∵y=-x2+4x+12=-(x-2)2+16,
∴对称轴x=2,
∴当0≤x≤1.5,12≤y≤15.75,台阶①高为10,即抛物线与台阶①无交点,P点不会落在台阶①处,
当1.5<x≤3,15≤y≤16,台阶②高为9,即抛物线与台阶②无交点,P点不会落在台阶②处,
当3<x≤4.5,9.75≤y≤15,台阶③高为8,即抛物线与台阶③无交点,P点不会落在台阶③处,
当4.5<x≤6,0≤y≤9.75,台阶④高为7,即抛物线与台阶④处存在交点,P点落在台阶④处,
∴令y=-(x-2)2+16=7,
∴解得x=5或-1(舍去,不符合题意),
∴此时落点P的坐标为(5,7).
【分析】如图所示,以BD的延长线为y轴,AB所在直线为x轴建立平面直角坐标系,由每个台阶的高、宽分别是1和1.5,第一个台阶到x轴距离BD=10,可将①~⑤个台阶的x范围及高度y求出,再结合抛物线的增减性,求出每个范围内的对应的y的范围,再结合每个台阶的高度即可判断出P点所落的台阶,将对应的高度y代入抛物线解析式可求出对应的x值,即可解决问题.
4.【答案】9
【解析】【解答】解:由题意得
当,,
化简得:,
解得:,(舍去),
故答案为:9.
【分析】令y=0,求出x的值,进而可得小豪此次投掷的成绩.
5.【答案】
【解析】【解答】解:∵OB=90dm,OA=2AB,
∴OA=OB=60dm,AB=30dm,
∴第一次反弹后抛物线的对称轴为x=30,顶点坐标为(30,h1)
∴设第一次反弹后的抛物线解析式为y=a(x-30)2+h1,
∵第一次反弹后抛物线过原点,
∴a(0-30)2+h1=0,
解得:h1=-900a,
又∵每次反弹后保持相同的抛物线形状,
∴设第二次反弹后的抛物线解析式为y=a(x-m)2+h2,
∵BC=h1,
∴BC=-600a,
∴C点坐标为(90,-600a)
∵抛物线过A,C两点,
∴,
整理,解得: ,
∴.
故答案为:.
【分析】易知OA及AB的长度,从而得第一次反弹后抛物线的对称轴为x=30dm,顶点坐标为(30,h1),设第一次反弹后的抛物线解析式为y=a(x-30)2+h1,由第一次反弹后抛物线过原点,可求出h1=-900a;根据每次反弹后保持相同的抛物线形状,设第二次反弹后的抛物线解析式为y=a(x-m)2+h2,再由BC=h1,得BC=-600a,即点C(90,-600a),把A,C两点坐标代入函数解析式可解出h2的值,即可求得的值.
6.【答案】(1)解:50 0.01×502=50 0.01×2500=25,所以球上升的高度是25m
(2)解:依题意有d 0.01d2=16,
解得d1=20,d2=80(舍去).
故球的水平距离是20m.
【解析】【分析】(1)把d=50代入函数式求h值,即可解答;
(2)令y=16,解关于x的一元二次方程,因为是求球的高度第一次达到16m时的水平距离,取较小值即可.
7.【答案】(1)解:依题意,顶点,
设抛物线的函数表达式为,
将代入,得.解之,得.
∴抛物线的函数表达式为.
(2)解:令,得.
解之,得.
∴.
【解析】【分析】(1)由题意可得P(5,9),设抛物线的解析式为y=a(x-5)2+9,将(0,0)代入求出a的值,据此可得抛物线的解析式;
(2)令y=6,求出x的值,据此可得点A、B的坐标.
8.【答案】(1)解:当y=0时,,
解得:x1=﹣1(舍去),x2=11,
∴点D的坐标为(11,0),
∴OD=11m.
∵从A点向四周喷水,喷出的水柱为抛物线,且形状相同,
∴OC=OD=11m,
∴CD=OC+OD=22m.
(2)解:∵,,
当x=10时,,
∴点F(10,)
∴雕塑EF的高为米.
【解析】【分析】(1)令y=0,求出x的值,可得D(11,0),则OD=11m,由题意可得OC=OD=11m,然后根据CD=OC+OD进行计算;
(2)令x=10,求出y的值,可得点F的坐标,据此解答.
9.【答案】(1)解:由题意,该抛物线过O(0,0)、M(12,0),
∴该抛物线的对称轴为直线x=6,顶点坐标为P(6,6),
设该抛物线的解析式为y=a(x-6)2+6,
将点O(0,0)代入,得:36a+6=0,解得:a= ,
∴该抛物线的解析式为y= (x-6)2+6= x2+2x;
(2)解:∵AD﹣DC﹣CB组成的是矩形“支撑架”,
∴AD=CB=4,
令y=4,由4= x2+2x得:x2-12x+24=0,
解得: , ,
∴C( ,4),D( ,4),
∴CD= -( )= ,
∴AD+DC+CB=4+4+ =8+ ,
∴这个“支撑架”总长是(8+ )米.
【解析】【分析】(1)由题意可知该抛物线过O(0,0)、M(12,0),求出中点坐标可得对称轴以及顶点坐标,设该抛物线的解析式为y=a(x-6)2+6,将O(0,0)代入求出a的值,据此可得抛物线的解析式;
(2)由题意可得AD=CB=4,令y=4,求出x的值,可得点C、D的坐标,然后求出CD,接下来求出AD+DC+CB即可.
10.【答案】(1)解:由题意设抛物线的解析式为y=a(x-6)2+12,
将点(0,0)代入,得36a+12=0,
解得a=,
∴抛物线的解析式为y=(x-6)2+12=x2+4x;
(2)解:能越过,理由如下:
∵山坡OA的坡度为1:3,
∴AE:OE=1:3,
∵OE=9米,
∴AE=3米,
当x=9时,y=(9-6)2+12=9,
∵3+5=8<9,
∴小刚投出的手榴弹能越过这棵树;
(3)解:由(2)知A的坐标为(9,3),
∴直线OA的解析式为,
作直线MNy轴,交抛物线于点M,交直线OA于点N,
设点M(x,x2+4x),则点N的坐标为(x,x),
∴MN=-x2+4x-x=,
∴当x=时,MN有最大值,最大值为,
∴飞行的过程中手榴弹离山坡的最大高度是米.
【解析】【分析】(1)设抛物线的解析式为y=a(x-6)2+12,将点(0,0)代入求出a的值即可;
(2)先将x=9代入y=(9-6)2+12,求出y=9,再结合3+5=8<9,可得小刚投出的手榴弹能越过这棵树;
(3)作直线MNy轴,交抛物线于点M,交直线OA于点N,设点M(x,x2+4x),则点N的坐标为(x,x),利用两点之间的距离公式可得MN=-x2+4x-x=,再利用二次函数的性质求解即可。
11.【答案】(1)解:当,时,.
(2)解:∵,
∵-5<0
∴当时,h取到最大值,.
答:球从弹起到最高点需要1秒,最高点的高度为5米.
(3)解:当时,,解得,.则对称轴为x=1
根据题意可知在球弹起后1.5秒时遇到夹板.
因为球遇到夹板弹起的速度与下落时恰好碰到夹板的速度大小相同,所以小球再次弹起,经过0.5秒后到达最高点,再经过1秒后落地,所以球从最初弹起到落回地面的时间为.
【解析】【分析】(1)令v0=10m/s、g=10m/s2即可得到h与t的关系式;
(2)将h与t的关系式化为顶点式,根据二次函数的性质可得h的最大值以及对应的t的值;
(3)令h=3.75,求出t的值,据此解答.
12.【答案】(1)解:∵ ,
当x=0时,
=.
∴雕塑OA高为m;
(2)解:设,
∴(x-11)(x+1)=0,
解得x=11或-1,
∴OD=11m,
∴CD=2OD=22m,
即落水点C、D之间的距离为22m ;
(3)解:∵OE=10m,
∴x=10,
∴
=,
∵1.8=,
∴>1.8,
∴ 顶部不会碰到水柱 .
【解析】【分析】(1)令x=0,代入函数式求出点A的坐标,即可解答;
(2)令y=0,求出抛物线与x轴的交点坐标,则可求出OD的距离,再根据对称性求CD的长即可;
(3)利用二次函数式计算出x=10时的函数值,再与EF的长进行比较可得结论.
13.【答案】(1)解:由题意可设 关于t的二次函数关系式为
因为当t=1,2时,h=15,20
,
解得:
∴ 关于t的二次函数关系式为 .
(2)解:当h=0时, =0,解得
∴小球从飞出到落地所用的时间为4s.
(3)解:小球的飞行高度不能达到20.5m
理由如下:
当h=20.5时, ,方程即为
,∴此方程无实数根.
即小球飞行的高度不能达到20.5m
【解析】【分析】(1)设 关于t的二次函数关系式为 ,由题意得当t=1,2时,h=15,20,再利用待定系数法求得 关于t的二次函数关系式即可;
(2)由(1)求得的 关于t的二次函数关系式,当h=0时,求得对应的时间,即可确定小球从飞出到落地所用的时间;
(3)当h=20.5时,-5t2+20t=20.5,整理方程并求出根的判别式的值小于零,从而得方程无实数根,即小球的飞行高度不能达到20.5m,即可求解.
14.【答案】(1)解:∵ ,
∴当 时,
∴当 时, 有最大值 ,
∴当 时, 有最大值30cm.
(2)解:∵s2=4h(30﹣h),
设存在a,b,使两孔射出水的射程相同,则有:
4a(30﹣a)=4b(30﹣b),
∴ ,
∴ ,
∴(a+b)(a﹣b)=30(a﹣b),
∴(a﹣b)(a+b﹣30)=0,
∴a﹣b=0,或a+b﹣30=0,
∴a=b或a+b=30
(3)解:设垫高的高度为 ,则
∴当 时, ,
∴ ,此时 .当 时,即 时, 时, , ,
∴m=19.2(舍弃).
∴垫高的高度为18cm,小孔离水面的竖直距离为24cm.
【解析】【分析】(1)根据题意求出当H=30cm时,s2=4h(30-h),再根据二次函数的性质得出s2的最大值,再求出算术平方根,即可得出答案;
(2)根据题意得出4a(30﹣a)=4b(30﹣b),再变形为(a﹣b)(a+b﹣30)=0,得出a=b或a+b=30,即可得出答案;
(3) 设垫高的高度为mcm,得出s2=4h(30+m-h),再根据二次函数的性质得出当h=时,smax=30+m=30+18,得出m=18,从而求出h=24,即可得出答案.
15.【答案】(1)解:设大孔抛物线的解析式为y=ax2+6,把点A( 5,0)代入解析式解得,
,
解得:,
∴函数解析式为
(2)解:把代入函数解析式得:
,
∵,
∴这艘船在正常水位时,能安全通过拱桥大孔
(3)解:∵NC=4,
∴把代入得:,
解得:,
∴E、F两个点的横坐标分别为:,,
当水位上涨到刚好淹没小孔时,大孔的水面宽度EF为:
【解析】【分析】(1)利用待定系数法即可求出大孔抛物线的解析式;
(2)求出x=2时y的值,与4.5做差,比较差与0.5的大小即可;
(3)求出E、F的坐标,即可得解。
16.【答案】(1)解:;
∵与y轴交于点A,
∴,.由题意可知,抛物线经过点(4,8),
∴,解得.
∴抛物线的函数表达式;
∵小球与小山丘的竖直距离为1米,∴,
解得:(不合题意,舍去),,
∴当小球与小山丘的竖直距离为1米时,小球离B处的水平距离为12米;
(2)解:将代入抛物线,得,
∴最远着陆点在小山丘外的平地上,其坐标为(15,0)
将代入抛物线,得,
解得:
∵抛物线,∴小山丘顶坐标为,
∵当小球飞行到小山丘顶正上方,且与顶部距离不小于米时,
∴,解得:
∴b的取值范围是.
∵,∴抛物线,∴的顶点坐标为,
∵,∴当时,有最小值为.
∴小球飞行路线的项点到x轴距离的最小值为米;
(3)解:b的取值范围:.
【解析】【解答】解:(1)由题意可得点B的坐标为,
将代入中,
解得;
解:(3)∵抛物线
当时,,
∴,
∵,,∴,
当时,,
∴与CD的交点坐标为
若小球恰好落入该装置内(不触碰装置侧壁),
则当时,,解得,
当时,,解得;
故b的取值范围:.
【分析】(1)由题意可得B(0,4),代入解析式可得c=4,又抛物线经过点(4,8),可得,求出,再根据题意列出方程求出x的值即可;
(2)将代入抛物线,得,求出,再根据题意列出求出可得,再求出的顶点坐标为,再结合可得当时,有最小值为;
(3)由题意可知,先求出与CD的交点坐标为,再分别将x=14和x=13代入求出,,即可得到。
17.【答案】(1)解:由图可知,点A坐标为(-12,-6),点B坐标为(12,-6),点O坐标为(0,0)
设抛物线的解析式为y=ax2+bx+c
将A,B,O代入解析式,得
解得
∴抛物线的解析式为y=-x2
(2)解:①∵=
∵>0
当x=-6时,y有最小值,且最小值为1
∵左、右两条抛物线关于轴对称
∴最低点之间的距离为2×6=12m
②令安全绳长度为wm,则
w=
=
=
∵>0
∴当x=-4时,w有最小值,且最小值为2
故安全绳长度最小值为2m.
【解析】【分析】(1)设抛物线的解析式为y=ax2+bx+c,将点B、A、O的坐标代入求出a、b、c的值即可;
(2)①利用配方法将变形为,再求解即可;
②令安全绳长度为wm,则,再利用二次函数的性质求解即可。
18.【答案】(1)解:
(2)3
(3)解:设抛物线的解析式为,
将(5,0)代入,得,
,
解得,,
∴(0≤x≤5),
(4)解:符合要求,理由:
设船的横断面为矩形ABCD,行驶时使船的中轴线在抛物线形水流的对称轴上,设直线AB与抛物线交点为E(1,m),则
,
符合要求
【解析】【解答】解:(2)根据图象看出,水流最高点距离湖面的高度是3米;
故答案为3;
【分析】(1)先建立平面直角坐标系,再利用描点法作出函数的图象即可;
(2)根据函数图象直接求解即可;
(3)利用待定系数法求出函数解析式即可;
(4)设船的横断面为矩形ABCD,行驶时使船的中轴线在抛物线形水流的对称轴上,设直线AB与抛物线交点为E(1,m),求出m的值并比较大小即可。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
二次函数应用(喷水、拱桥、投球问题)
一、填空题
1.(2022·广安)如图是抛物线形拱桥,当拱顶离水面2米时,水面宽6米,水面下降 米,水面宽8米.
2.(2022·武威)如图,以一定的速度将小球沿与地面成一定角度的方向击出时,小球的飞行路线是一条抛物线.若不考虑空气阻力,小球的飞行高度 (单位:m)与飞行时间 (单位:s)之间具有函数关系: ,则当小球飞行高度达到最高时,飞行时间 s.
3.(2022九下·长兴月考)如图是王明正在设计的一动画示意图,×轴上依次有A,B,C三个点,且AB=2,在BC上方有五个台阶(各拐角均为90°),每个台阶的高、宽分别是1和1.5,第一个台阶到x轴距离BD=10.从点A处向右,上方沿抛物线y=-x2+4x+12发出一个带光的点P.当点P落在台阶上时,落点的坐标是 .
4.(2022·衢州模拟)为了在体育中考中取得更好的成绩,小豪积极训练,体育老师对小豪投掷实心球的录像进行技术分析,如图,发现实心球在行进过程中高度y(m)与水平距离x(m)之间的关系为,由此可知小豪此次投掷的成绩是 m.
5.(2022·玉环模拟)斜抛小球,小球触地后呈抛物线反弹,每次反弹后保持相同的抛物线形状(开口方向与开口大小前后一致),第一次反弹后的最大高度为 ,第二次反弹后的最大高度为 ,第二次反弹后,小球越过最高点落在垂直于地面的挡板C处,且离地高度 ,若 ,则 为 .
二、综合题
6.(2022八下·杭州月考)一高尔夫球手某次击出一个高尔夫球的高度h(m)和经过的水平距离d(m)可用公式h=-0.01d2 +d来估计.
(1)当球的水平距离达到50m时.球上升的高度是多少?
(2)当球的高度第一次达到16m时.球的水平距离是多少?
7.(2022·陕西)现要修建一条隧道,其截面为抛物线型,如图所示,线段表示水平的路面,以O为坐标原点,以所在直线为x轴,以过点O垂直于x轴的直线为y轴,建立平面直角坐标系.根据设计要求:,该抛物线的顶点P到的距离为.
(1)求满足设计要求的抛物线的函数表达式;
(2)现需在这一隧道内壁上安装照明灯,如图所示,即在该抛物线上的点A、B处分别安装照明灯.已知点A、B到的距离均为,求点A、B的坐标.
8.(2021九上·全椒期末)某游乐场的圆形喷水池中心O有一雕塑OA,从A点向四周喷水,喷出的水柱为抛物线,且形状相同。如图,以水平方向为x轴,点O为原点建立直角坐标系,点A在y轴上,x轴上的点C、D为水柱的落水点,水柱所在抛物线(第一象限部分)的函数表达式为.
(1)求落水点C、D之间的距离;
(2)若需在OD上离O点10米的E处竖立雕塑EF,,且雕塑的顶部刚好碰到水柱,求雕塑EF的高.
9.(2021九上·海州期末)如图,某公路隧道横截面为抛物线,其最大高度6米,底部宽度OM为12米,现以O点为原点,OM所在的直线为x轴建立直角坐标系.
(1)求这条抛物线的解析式;
(2)若要搭建一个由AD﹣DC﹣CB组成的矩形“支撑架”,已知支架的高度为4米,则这个“支撑架”总长是多少米?
10.(2022·青岛模拟)手榴弹作为一种威力较大,体积较小,方便携带的武器,在战争中能发挥重要作用,然而想把手榴弹扔远,并不是一件容易的事.军训中,借助小山坡的有利地势,小刚在教官的指导下用模拟弹进行一次试投:如图所示,把小刚投出的手榴弹的运动路线看做一条抛物线,手榴弹飞行的最大高度为12米,此时它的水平飞行距离为6米,山坡OA的坡度为1:3.
(1)求这条抛物线的表达式;
(2)山坡上A处的水平距离OE为9米,A处有一棵树,树高5米,则小刚投出的手榴弹能否越过这棵树?请说明理由;
(3)求飞行的过程中手榴弹离山坡的最大高度是多少米.
11.(2022·新昌模拟)一个球从地面竖直向上弹起时的速度为10m/s,经过t(s)时球的高度为h(m).已知物体竖直上抛运动中,(表示物体运动上弹开始的速度,g表示重力系数,取).
(1)写出h(m)关于t(s)的二次函数表达式.
(2)求球从弹起到最高点需要多少时间,最高点的高度是多少?
(3)若球在下落至处时,遇一夹板(这部分运动的函数图象如图所示),球以遇到夹板时的速度再次向上竖直弹起,然后落回地面.求球从最初10m/s弹起到落回地面的时间.
12.(2022九下·定海开学考)某游乐场的圆形喷水池中心O有一雕塑OA,从A点向四周喷水,喷出的水柱为抛物线,且形状相同.如图,以水平方向为x轴,点O为原点建立直角坐标系,点A在y轴上,x轴上的点C,D为水柱的落水点,水柱所在抛物线(第一象限部分)的函数表达式为
(1)求雕塑高OA.
(2)求落水点C,D之间的距离.
(3)若需要在OD上的点E处竖立雕塑EF,OE=10m,EF=1.8m,EF⊥OD.问:顶部F是否会碰到水柱?请通过计算说明.
13.(2022·上虞模拟)如图,以一定的速度将小球沿与地面成一定角度的方向击出时,小球的“飞行路线将是一条抛物线.如果不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有二次函数关系.小明在一次击球过程中测得一些数据,如下表所示.
根据相关信息解答下列问题.
飞行时间t/s 0 1 2
飞行高度h/m 0 15 20
(1)求小球的飞行高度h(单位:m)关于飞行时间t(单位:s)的二次函数关系式.
(2)小球从飞出到落地要用多少时间?
(3)小球的飞行高度能否达到20.5m?如果能,请求出相应的飞行时间;如果不能,请说明理由.
14.(2022九下·义乌月考)用各种盛水容器可以制作精致的家用流水景观(如图1).
科学原理:如图2,始终盛满水的圆柱体水桶水面离地面的高度为H(单位:cm),如果在离水面竖直距离为h(单位:cm)的地方开大小合适的小孔,那么从小孔射出水的射程(水流落地点离小孔的水平距离)s(单位:cm)与h的关系式为s2=4h(H﹣h).
应用思考:现用高度为30cm的圆柱体塑料水瓶做相关研究,水瓶直立地面,通过连续注水保证它始终盛满水,在离水面竖直距离hcm处开一个小孔.
(1)写出s2与h的关系式;并求出当h为何值时,射程s有最大值,最大射程是多少?
(2)在侧面开两个小孔,这两个小孔离水面的竖直距离分别为a,b,要使两孔射出水的射程相同,求a,b之间的关系式;
(3)如果想通过垫高塑料水瓶,使射出水的最大射程增加18cm,求垫高的高度及小孔离水面的竖直距离.
15.(2022·河北模拟)如图所示.三孔桥横截面的三个孔是都呈抛物线形,两小孔形状、大小都相同.正常水位时,大孔水面宽度AB为10m,顶点M距水面6m(即),小孔顶点N距水面4m(即),建立如图所示的平面直角坐标系.
(1)求出大孔抛物线的解析式;
(2)现有一艘船高度是4.5m,宽度是4m,为了保证安全,船顶距离桥拱顶部至少0.5m,则这艘船在正常水位时能否安全通过拱桥大孔?
(3)当水位上涨到刚好淹没小孔时,求出此时大孔的水面宽度EF.
16.(2022·石家庄模拟)如图1的小山丘是科研部门的小球弹射实验场地,在小山丘一侧的山坡上建有小球弹射发射装置,另一侧建有圆柱形小球接收装置,如图2为实验场地的纵截面示意图,小山丘纵截面的外部轮廓线近似为抛物线的一部分,以小山丘纵截面与地面的交线为x轴,以过发射装置所在的直线AB为y轴,建立平面直角坐标系,发射装置底部在轮廓线的点A处,距离地面为1米,在发射装置3米的点B处是发射点,已知小山丘纵截面的外部轮廓线为,从发射装置的发射点弹射一个小球(忽略空气阻力)时,小球的飞行路线为一段抛物线.
(1)直接写出c的值,当小球离B处的水平距离和竖直距离都为4米时,求b的值,并求小球到小山丘的竖直距离为1米时,小球离B处的水平距离;
(2)若小球最远着陆点到y轴的距离为15米,当小球飞行到小山丘顶的正上方,且与顶部距离不小于米时,求b的取值范围,并求小球飞行路线的顶点到x轴距离的最小值;
(3)圆柱形小球接收装置的最大截面为矩形CDEF,已知点E在上,其横坐标为14,轴,,.若小球恰好落入该装置内(不触碰装置侧壁),请直接写出b的取值范围.
17.(2022·胶州模拟)如图1是一座抛物线型拱桥,图2是其在直角坐标系中的侧面示意图.在正常水位时水面宽,此时水面离桥拱顶部的距离为.
(1)按如图2所示的直角坐标系,求此抛物线的函数表达式;
(2)如图3,因某种需要,在桥拱顶部及桥的两端树立了三根支柱,,架设钢缆,在钢缆和桥面之间竖直悬挂若干安全绳,过相邻支柱顶端的钢缆具有相同的抛物线形状,且左、右两条抛物线关于轴对称,左面钢缆抛物线可以用表示.
①求左、右面两条钢缆的最低点之间的距离是多少?
②求安全绳长度(钢缆和桥面之间距离)的最小值是多少?
18.(2022·顺义模拟)某公园内的人工湖里有一组小型喷泉,水柱从位于湖面上方的水枪喷出,水柱落于湖面的路径形状是抛物线.现测量出如下数据,在距离水枪水平距离为d米的地点,水柱距离湖面高度为h米.
d(米) 0 0.5 2.0 3.5 5
h(米) 1.67 2. 25 3.00 2. 25 0
请解决以下问题:
(1)在下面网格中建立适当的平面直角坐标系,根据已知数据描点,并用平滑的曲线连接;
(2)请结合所画图象,水柱最高点距离湖面的高度是 米;
(3)求抛物线的表达式,并写出自变量的取值范围;
(4)现有一游船宽度为2米,顶棚到湖面的高度为2.5米.要求游船从喷泉水柱中间通过时,顶棚不碰到水柱.请问游船是否能符合上述要求通过?并说明理由.
答案解析部分
1.【答案】
【解析】【解答】解:建立平面直角坐标系,设横轴x通过AB,纵轴y通过AB中点O且通过C点,则通过画图可得知O为原点,由题意可得:AO=OB=3米,C坐标为(0,2),
通过以上条件可设顶点式y=ax2+2,把点A点坐标(3,0)代入得,
∴,
∴,
∴抛物线解析式为:;
当水面下降,水面宽为8米时,有
把代入解析式,得;
∴水面下降米;
故答案为:.
【分析】建立平面直角坐标系,设横轴x通过AB,纵轴y通过AB中点O且通过C点,则通过画图可得知O为原点,由题意可得:AO=OB=3米,C(0,2),设y=ax2+2,把A点坐标代入求出a的值,据此可得抛物线的解析式,令x=4,求出y的值,据此解答.
2.【答案】2
【解析】【解答】解:∵h=-5t2+20t=-5(t-2)2+20,且-5<0,
∴当t=2时,h取最大值20.
故答案为:2.
【分析】将h与t的函数关系式化为顶点式,据此可得h的最大值.
3.【答案】(5,7)
【解析】【解答】解:如图所示,以BD的延长线为y轴,AB所在直线为x轴建立平面直角坐标系,
∵每个台阶的高、宽分别是1和1.5,第一个台阶到x轴距离BD=10,
∴对于①~⑤个台阶有:
台阶①:0≤x≤1.5,y=10;
台阶②:1.5<x≤3,y=9;
台阶③:3<x≤4.5,y=8;
台阶④:4.5<x≤6,y=7;
台阶⑤:6<x≤7.5,y=6,
∵y=-x2+4x+12=-(x-2)2+16,
∴对称轴x=2,
∴当0≤x≤1.5,12≤y≤15.75,台阶①高为10,即抛物线与台阶①无交点,P点不会落在台阶①处,
当1.5<x≤3,15≤y≤16,台阶②高为9,即抛物线与台阶②无交点,P点不会落在台阶②处,
当3<x≤4.5,9.75≤y≤15,台阶③高为8,即抛物线与台阶③无交点,P点不会落在台阶③处,
当4.5<x≤6,0≤y≤9.75,台阶④高为7,即抛物线与台阶④处存在交点,P点落在台阶④处,
∴令y=-(x-2)2+16=7,
∴解得x=5或-1(舍去,不符合题意),
∴此时落点P的坐标为(5,7).
【分析】如图所示,以BD的延长线为y轴,AB所在直线为x轴建立平面直角坐标系,由每个台阶的高、宽分别是1和1.5,第一个台阶到x轴距离BD=10,可将①~⑤个台阶的x范围及高度y求出,再结合抛物线的增减性,求出每个范围内的对应的y的范围,再结合每个台阶的高度即可判断出P点所落的台阶,将对应的高度y代入抛物线解析式可求出对应的x值,即可解决问题.
4.【答案】9
【解析】【解答】解:由题意得
当,,
化简得:,
解得:,(舍去),
故答案为:9.
【分析】令y=0,求出x的值,进而可得小豪此次投掷的成绩.
5.【答案】
【解析】【解答】解:∵OB=90dm,OA=2AB,
∴OA=OB=60dm,AB=30dm,
∴第一次反弹后抛物线的对称轴为x=30,顶点坐标为(30,h1)
∴设第一次反弹后的抛物线解析式为y=a(x-30)2+h1,
∵第一次反弹后抛物线过原点,
∴a(0-30)2+h1=0,
解得:h1=-900a,
又∵每次反弹后保持相同的抛物线形状,
∴设第二次反弹后的抛物线解析式为y=a(x-m)2+h2,
∵BC=h1,
∴BC=-600a,
∴C点坐标为(90,-600a)
∵抛物线过A,C两点,
∴,
整理,解得: ,
∴.
故答案为:.
【分析】易知OA及AB的长度,从而得第一次反弹后抛物线的对称轴为x=30dm,顶点坐标为(30,h1),设第一次反弹后的抛物线解析式为y=a(x-30)2+h1,由第一次反弹后抛物线过原点,可求出h1=-900a;根据每次反弹后保持相同的抛物线形状,设第二次反弹后的抛物线解析式为y=a(x-m)2+h2,再由BC=h1,得BC=-600a,即点C(90,-600a),把A,C两点坐标代入函数解析式可解出h2的值,即可求得的值.
6.【答案】(1)解:50 0.01×502=50 0.01×2500=25,所以球上升的高度是25m
(2)解:依题意有d 0.01d2=16,
解得d1=20,d2=80(舍去).
故球的水平距离是20m.
【解析】【分析】(1)把d=50代入函数式求h值,即可解答;
(2)令y=16,解关于x的一元二次方程,因为是求球的高度第一次达到16m时的水平距离,取较小值即可.
7.【答案】(1)解:依题意,顶点,
设抛物线的函数表达式为,
将代入,得.解之,得.
∴抛物线的函数表达式为.
(2)解:令,得.
解之,得.
∴.
【解析】【分析】(1)由题意可得P(5,9),设抛物线的解析式为y=a(x-5)2+9,将(0,0)代入求出a的值,据此可得抛物线的解析式;
(2)令y=6,求出x的值,据此可得点A、B的坐标.
8.【答案】(1)解:当y=0时,,
解得:x1=﹣1(舍去),x2=11,
∴点D的坐标为(11,0),
∴OD=11m.
∵从A点向四周喷水,喷出的水柱为抛物线,且形状相同,
∴OC=OD=11m,
∴CD=OC+OD=22m.
(2)解:∵,,
当x=10时,,
∴点F(10,)
∴雕塑EF的高为米.
【解析】【分析】(1)令y=0,求出x的值,可得D(11,0),则OD=11m,由题意可得OC=OD=11m,然后根据CD=OC+OD进行计算;
(2)令x=10,求出y的值,可得点F的坐标,据此解答.
9.【答案】(1)解:由题意,该抛物线过O(0,0)、M(12,0),
∴该抛物线的对称轴为直线x=6,顶点坐标为P(6,6),
设该抛物线的解析式为y=a(x-6)2+6,
将点O(0,0)代入,得:36a+6=0,解得:a= ,
∴该抛物线的解析式为y= (x-6)2+6= x2+2x;
(2)解:∵AD﹣DC﹣CB组成的是矩形“支撑架”,
∴AD=CB=4,
令y=4,由4= x2+2x得:x2-12x+24=0,
解得: , ,
∴C( ,4),D( ,4),
∴CD= -( )= ,
∴AD+DC+CB=4+4+ =8+ ,
∴这个“支撑架”总长是(8+ )米.
【解析】【分析】(1)由题意可知该抛物线过O(0,0)、M(12,0),求出中点坐标可得对称轴以及顶点坐标,设该抛物线的解析式为y=a(x-6)2+6,将O(0,0)代入求出a的值,据此可得抛物线的解析式;
(2)由题意可得AD=CB=4,令y=4,求出x的值,可得点C、D的坐标,然后求出CD,接下来求出AD+DC+CB即可.
10.【答案】(1)解:由题意设抛物线的解析式为y=a(x-6)2+12,
将点(0,0)代入,得36a+12=0,
解得a=,
∴抛物线的解析式为y=(x-6)2+12=x2+4x;
(2)解:能越过,理由如下:
∵山坡OA的坡度为1:3,
∴AE:OE=1:3,
∵OE=9米,
∴AE=3米,
当x=9时,y=(9-6)2+12=9,
∵3+5=8<9,
∴小刚投出的手榴弹能越过这棵树;
(3)解:由(2)知A的坐标为(9,3),
∴直线OA的解析式为,
作直线MNy轴,交抛物线于点M,交直线OA于点N,
设点M(x,x2+4x),则点N的坐标为(x,x),
∴MN=-x2+4x-x=,
∴当x=时,MN有最大值,最大值为,
∴飞行的过程中手榴弹离山坡的最大高度是米.
【解析】【分析】(1)设抛物线的解析式为y=a(x-6)2+12,将点(0,0)代入求出a的值即可;
(2)先将x=9代入y=(9-6)2+12,求出y=9,再结合3+5=8<9,可得小刚投出的手榴弹能越过这棵树;
(3)作直线MNy轴,交抛物线于点M,交直线OA于点N,设点M(x,x2+4x),则点N的坐标为(x,x),利用两点之间的距离公式可得MN=-x2+4x-x=,再利用二次函数的性质求解即可。
11.【答案】(1)解:当,时,.
(2)解:∵,
∵-5<0
∴当时,h取到最大值,.
答:球从弹起到最高点需要1秒,最高点的高度为5米.
(3)解:当时,,解得,.则对称轴为x=1
根据题意可知在球弹起后1.5秒时遇到夹板.
因为球遇到夹板弹起的速度与下落时恰好碰到夹板的速度大小相同,所以小球再次弹起,经过0.5秒后到达最高点,再经过1秒后落地,所以球从最初弹起到落回地面的时间为.
【解析】【分析】(1)令v0=10m/s、g=10m/s2即可得到h与t的关系式;
(2)将h与t的关系式化为顶点式,根据二次函数的性质可得h的最大值以及对应的t的值;
(3)令h=3.75,求出t的值,据此解答.
12.【答案】(1)解:∵ ,
当x=0时,
=.
∴雕塑OA高为m;
(2)解:设,
∴(x-11)(x+1)=0,
解得x=11或-1,
∴OD=11m,
∴CD=2OD=22m,
即落水点C、D之间的距离为22m ;
(3)解:∵OE=10m,
∴x=10,
∴
=,
∵1.8=,
∴>1.8,
∴ 顶部不会碰到水柱 .
【解析】【分析】(1)令x=0,代入函数式求出点A的坐标,即可解答;
(2)令y=0,求出抛物线与x轴的交点坐标,则可求出OD的距离,再根据对称性求CD的长即可;
(3)利用二次函数式计算出x=10时的函数值,再与EF的长进行比较可得结论.
13.【答案】(1)解:由题意可设 关于t的二次函数关系式为
因为当t=1,2时,h=15,20
,
解得:
∴ 关于t的二次函数关系式为 .
(2)解:当h=0时, =0,解得
∴小球从飞出到落地所用的时间为4s.
(3)解:小球的飞行高度不能达到20.5m
理由如下:
当h=20.5时, ,方程即为
,∴此方程无实数根.
即小球飞行的高度不能达到20.5m
【解析】【分析】(1)设 关于t的二次函数关系式为 ,由题意得当t=1,2时,h=15,20,再利用待定系数法求得 关于t的二次函数关系式即可;
(2)由(1)求得的 关于t的二次函数关系式,当h=0时,求得对应的时间,即可确定小球从飞出到落地所用的时间;
(3)当h=20.5时,-5t2+20t=20.5,整理方程并求出根的判别式的值小于零,从而得方程无实数根,即小球的飞行高度不能达到20.5m,即可求解.
14.【答案】(1)解:∵ ,
∴当 时,
∴当 时, 有最大值 ,
∴当 时, 有最大值30cm.
(2)解:∵s2=4h(30﹣h),
设存在a,b,使两孔射出水的射程相同,则有:
4a(30﹣a)=4b(30﹣b),
∴ ,
∴ ,
∴(a+b)(a﹣b)=30(a﹣b),
∴(a﹣b)(a+b﹣30)=0,
∴a﹣b=0,或a+b﹣30=0,
∴a=b或a+b=30
(3)解:设垫高的高度为 ,则
∴当 时, ,
∴ ,此时 .当 时,即 时, 时, , ,
∴m=19.2(舍弃).
∴垫高的高度为18cm,小孔离水面的竖直距离为24cm.
【解析】【分析】(1)根据题意求出当H=30cm时,s2=4h(30-h),再根据二次函数的性质得出s2的最大值,再求出算术平方根,即可得出答案;
(2)根据题意得出4a(30﹣a)=4b(30﹣b),再变形为(a﹣b)(a+b﹣30)=0,得出a=b或a+b=30,即可得出答案;
(3) 设垫高的高度为mcm,得出s2=4h(30+m-h),再根据二次函数的性质得出当h=时,smax=30+m=30+18,得出m=18,从而求出h=24,即可得出答案.
15.【答案】(1)解:设大孔抛物线的解析式为y=ax2+6,把点A( 5,0)代入解析式解得,
,
解得:,
∴函数解析式为
(2)解:把代入函数解析式得:
,
∵,
∴这艘船在正常水位时,能安全通过拱桥大孔
(3)解:∵NC=4,
∴把代入得:,
解得:,
∴E、F两个点的横坐标分别为:,,
当水位上涨到刚好淹没小孔时,大孔的水面宽度EF为:
【解析】【分析】(1)利用待定系数法即可求出大孔抛物线的解析式;
(2)求出x=2时y的值,与4.5做差,比较差与0.5的大小即可;
(3)求出E、F的坐标,即可得解。
16.【答案】(1)解:;
∵与y轴交于点A,
∴,.由题意可知,抛物线经过点(4,8),
∴,解得.
∴抛物线的函数表达式;
∵小球与小山丘的竖直距离为1米,∴,
解得:(不合题意,舍去),,
∴当小球与小山丘的竖直距离为1米时,小球离B处的水平距离为12米;
(2)解:将代入抛物线,得,
∴最远着陆点在小山丘外的平地上,其坐标为(15,0)
将代入抛物线,得,
解得:
∵抛物线,∴小山丘顶坐标为,
∵当小球飞行到小山丘顶正上方,且与顶部距离不小于米时,
∴,解得:
∴b的取值范围是.
∵,∴抛物线,∴的顶点坐标为,
∵,∴当时,有最小值为.
∴小球飞行路线的项点到x轴距离的最小值为米;
(3)解:b的取值范围:.
【解析】【解答】解:(1)由题意可得点B的坐标为,
将代入中,
解得;
解:(3)∵抛物线
当时,,
∴,
∵,,∴,
当时,,
∴与CD的交点坐标为
若小球恰好落入该装置内(不触碰装置侧壁),
则当时,,解得,
当时,,解得;
故b的取值范围:.
【分析】(1)由题意可得B(0,4),代入解析式可得c=4,又抛物线经过点(4,8),可得,求出,再根据题意列出方程求出x的值即可;
(2)将代入抛物线,得,求出,再根据题意列出求出可得,再求出的顶点坐标为,再结合可得当时,有最小值为;
(3)由题意可知,先求出与CD的交点坐标为,再分别将x=14和x=13代入求出,,即可得到。
17.【答案】(1)解:由图可知,点A坐标为(-12,-6),点B坐标为(12,-6),点O坐标为(0,0)
设抛物线的解析式为y=ax2+bx+c
将A,B,O代入解析式,得
解得
∴抛物线的解析式为y=-x2
(2)解:①∵=
∵>0
当x=-6时,y有最小值,且最小值为1
∵左、右两条抛物线关于轴对称
∴最低点之间的距离为2×6=12m
②令安全绳长度为wm,则
w=
=
=
∵>0
∴当x=-4时,w有最小值,且最小值为2
故安全绳长度最小值为2m.
【解析】【分析】(1)设抛物线的解析式为y=ax2+bx+c,将点B、A、O的坐标代入求出a、b、c的值即可;
(2)①利用配方法将变形为,再求解即可;
②令安全绳长度为wm,则,再利用二次函数的性质求解即可。
18.【答案】(1)解:
(2)3
(3)解:设抛物线的解析式为,
将(5,0)代入,得,
,
解得,,
∴(0≤x≤5),
(4)解:符合要求,理由:
设船的横断面为矩形ABCD,行驶时使船的中轴线在抛物线形水流的对称轴上,设直线AB与抛物线交点为E(1,m),则
,
符合要求
【解析】【解答】解:(2)根据图象看出,水流最高点距离湖面的高度是3米;
故答案为3;
【分析】(1)先建立平面直角坐标系,再利用描点法作出函数的图象即可;
(2)根据函数图象直接求解即可;
(3)利用待定系数法求出函数解析式即可;
(4)设船的横断面为矩形ABCD,行驶时使船的中轴线在抛物线形水流的对称轴上,设直线AB与抛物线交点为E(1,m),求出m的值并比较大小即可。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
